Вопрос 1

Счестность множества рациональных чисел, нечетность множества действительных (вещественных) чисел.

1. Th.: Множество рациональных чисел счетно.

Pr.: Составим таблицу чисел, содержащие все рац. числа.

n/m	0	1	-1	2	-2	3	-3	…
1	0/1	1/1	-1/1	2/1	-2/1	3/1	-3/1	…
2	0/2	½	-1/2	2/2	-2/2	3/2	-3/2	…
3	0/3	1/3	-1/3	2/3	-2/3	3/3	-3/3	…
4	0/4	1/4	-1/4	2/4	-2/4	3/4	-3/4	…
…	…	…	…	…	…	…	…	…

Двигаемся по таблице таким образом:

Нумеруя встречающиеся в клетках рациональные числа, пропуская, которые уже были. Очевидно, таким образом мы занумеруем все рациональные числа всеми натуральными, что и требовалось показать.

2. Th.: Множество всех точек отрезка [0,1] несчетно.

Pr.: Допустим противное. Тогда все точки отрезка [0,1] можно занумеровать: 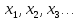Поделим отрезок [0,1] на три ровных отрезка и обозначим через 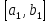один из них, свободный от точки 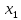. 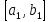на три равных отрезка и обозначим через 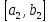один из них, свободный от точки 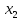. Продолжая процесс, получим систему вложенных отрезков 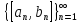. По теореме о вложенных отрезках существует точка c, принадлежащая всем отрезкам системы. Эта точка c не совпадает ни с одной из занумерованных точек 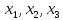… , так как произвольная из них 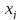не содержится в отрезке 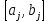, в то время как с содержится в этом отрезке. Допуская, что все точки отрезка [0,1] занумерованы, мы пришли к противоречию, найдя точку 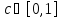, отличную от занумерованных. Это противоречит нашему предположению. Теорема доказана.

Вопрос 2

Теорема о (точной) верхней грани.

Def.: Множество 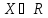называется ограниченным сверху, если существует число b такое, что .

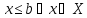Th.: Числовое множество не может иметь более одной верхней грани.

Pr.: Допуская противное, предположим, что каждое из чисел b и b’ (b≠b’) является верхней гранью множества Х. Пусть для определенности, b’<b. Тогда в силу того, что b=supX, из определения верхней грани следует, что для числа 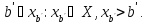Но тогда b’ не является верхней гранью Х. Из полученного противоречия следует ошибочность предположения и утверждение теоремы.

Вопрос 3

Бесконечно малые последовательности, их свойства.

Def.: Последовательность 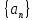называется бесконечно малой, если

L.: Сумма, разность и произведение бесконечно малых последовательностей являются бесконечно малыми последовательностями.

Вопрос 4

Единственность предела сходящейся последовательности. Ограниченность сходящейся последовательности.

Th.: Числовая последовательность не может иметь в 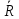более одного предела.

Pr.: Предполагая противное, допустим, что для данной последовательности {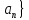 каждый из двух различных элементов 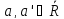является пределом. Пусть 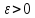столь мало, что 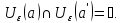Тогда по определению предела 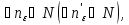при котором 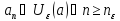(та же формула для штриха).

Положив 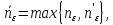получаем, что 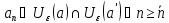, а это невозможно, так как это пересечение пусто. Теорема доказана.

Th.: Сходящаяся последовательность ограничена.

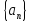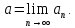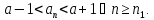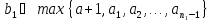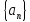Pr.: Пусть последовательность сходится и Тогда для , так что Пусть . Очевидно, что ограниченна сверху числом . Аналогично показывается, что 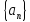ограничена снизу. Последовательность 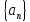ограничена в силу ее ограниченности сверху и снизу.