Лекція 10. Безперервні системи та їх моделі.

В залежності від природи та вигляду операторів та залежностей, що входять до виразу загальносистемної моделі, системи, які нею описуються, можуть мати досить відмінні властивості і відноситись до різних класів.

Наприклад, якщо оператори та задані на всій області визначення для змінної і виконуються умови відхилення на безкінечно малу величину часу

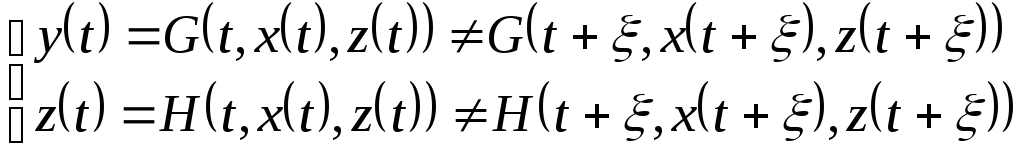; (1)

то система, що описується такою моделлю називається безперервною системою. Фактично, безперервність системи свідчить, що при зміні як часу, так і вхідного впливу на безкінечно малу величину, вихідна координата та внутрішній стан змінюються на безкінечно малу величину.

Безперервність – фундаментальна властивість систем, що відрізняє їх від великого класу так званих дискретних систем, які можуть бути описані і досліджені виключно в певні моменти часу, між якими знаходяться в стані невизначеності.

Безперервні системи найбільш зручні в описі та моделюванні, оскільки їх статика описується системами алгебраїчних рівнянь, а динаміка – системами диференційних рівнянь.

Оператори та для безперервних систем можуть бути записані у вигляді векторних диференційних рівнянь

; (2)

Оператори та можуть мати властивості однорідності (по відношенню до операції множення) та (або) адитивності (по відношенню до операції додавання). В першому випадку при множенні змінних на довільний коефіцієнт, він може бути винесений за знак оператора

; (3)

В другому випадку кожен з операторів може бути представлений сумою часткових операторів, що містить постійну і змінну складову

; (4)

Оскільки та (початкові значення вхідної змінної та внутрішнього стану в момент часу ) - константи, при диференціюванні вони виключаються із операторів згідно (2).

Якщо для операторів, що описують систему одночасно виконуються умови однорідності та адитивності, ця система є лінійною. Лінійність системи – також важлива її якість, яка дозволяє значно спрощувати її опис та моделювання, оскільки динамічні та статичні процеси в ній описуються рівняннями першого порядку.

Найбільш розглянутим і дослідженим класом систем є безперервні лінійні системи, робота яких може бути описана через (2) з урахуванням (3)-(4)

. (5)

де , , та - матриці коефіцієнтів, що в загальному випадку залежать від часу (частіше є константами). Дана модель надзвичайно проста, але навіть при її використанні необхідно знати велику кількість параметрів, що є коефіцієнтами моделі. Наприклад, якщо - кількість вхідних координат, - кількість вихідних, а - кількість змінних стану, то важливо пам’ятати про два показника складності системи:

сумарну розмірність (6)

кількість коефіцієнтів (7)

Тобто, вже при необхідно знати близько 50-100 коефіцієнтів. Якщо ж вони при цьому залежать від часу, задача неймовірно ускладнюється. Це є головною проблемою при моделюванні систем великої розмірності. Тому, при аналізі систем на практиці намагаються якомога сильніше зменшити коло факторів, що розглядаються (вхідних змінних) і величин, на які вони впливають (вихідних змінних) через доведення слабкості впливу тих чи інших речей на поведінку системи.

Стаціонарною називається система, інваріантна до часу. Тобто, якщо в оператори виходу та стану ввести зсув у часі на величину , поведінка системи не зміниться

; (8)

Інакше кажучи, в який момент часу ми не стали розглядати стаціонарну систему, при однаковій вхідній послідовності та однакових початкових умовах вона буде поводити себе однаково.

Всі розглянуті досі системи були детерміновані, оскільки оператори та ставили у однозначну відповідність набори , та . В реальності більшість систем є імовірнісними або стохастичними. В них значення вихідної величини при певних та описується набором значень, що має назву закону розподілу ймовірностей. В такому випадку оператори та замінюються мірами ймовірності та .

Надважкий процес аналізу подібних систем може бути спрощений використанням замість випадкових величин , та їх математичних очікувань, наприклад

. (9)

Але така заміна не завжди припустима, до того ж подібні розрахунки будуть мати скінчену точність (в техніці прийнято 95%).