1. Основні закони і співвідношення

 Рівняння гармонічного коливання має вигляд

або

,

де: x – зміщення коливної точки (чи центра мас тіла) від положення рівноваги; А – амплітуда; t – час;  – початкова фаза; ₀ – циклічна частота власних незгасаючих коливань (власна циклічна частота).

 Частота (лінійна)

,

період коливань

,

де N – число коливань за час t.

 Зв’язок циклічної частоти з періодом

.

 Формули для розрахунку періоду вільних незгасаючих механічних коливань різних осциляторів:

а) пружинного маятника

;

б) математичного маятника

;

в) фізичного маятника

.

Тут: m – маса маятника (у випадку а) – це маса матеріальної точки чи тіла, прикріпленого до пружини); k – жорсткість пружини; l – відстань від центра мас маятника до точки підвісу (у випадку б) ця величина співпадає з довжиною нитки); g – прискорення вільного падіння; L – зведена довжина фізичного маятника;

,

де І – момент інерції маятника відносно осі, що проходить через точку підвісу перпендикулярно до площини коливань центра мас.

 У випадку фізичного маятника рівняння коливань прийнято записувати через кут відхилення  від положення рівноваги (кутове зміщення)

.

 Кінетична енергія осцилятора

,

потенціальна енергія

,

повна механічна енергія

.

 При складанні двох однаково направлених гармонічних коливань однакової частоти одержується гармонічне коливання тієї ж частоти з амплітудою

та з початковою фазою , що задовільняє рівняння

.

Тут A₁ і A₂ – амплітуди вихідних коливань, ₁ та ₂ – початкові фази.

 При складанні двох взаємно перпендикулярних гармонічних коливань однакової частоти рівняння траєкторії результуючого руху має вигляд

,

А – амплітуда коливання по осі Ох, В – по осі Оу.

 Рівняння згасаючих коливань

,

де: А₀ – амплітуда при ;  – коефіцієнт згасання,  – циклічна частота згасаючих коливань,

.

 Логарифмічний декремент згасання

.

 Рівняння усталених вимушених коливань

,

де:  – циклічна частота зовнішньої періодично діючої сили;

;

;

F₀ – амплітудне значення змушувальної сили.

 Резонансна частота

.

 Рівняння плоскої хвилі, що поширюється вздовж осі Ох:

або

,

де: – зміщення коливної точки в момент часу t в точці простору з координатою х; А – амплітуда коливань;  – циклічна частота; v – модуль фазової швидкості хвилі;  – початкова фаза; – хвильове число; – довжина хвилі; Т – період коливань.

 Модуль швидкості звуку в рідині

,

де  – густина,  – адіабатична стисливість рідини.

 Модуль швидкості поширення звуку в газах (близьких до ідеального)

,

де  – коефіцієнт Пуасона (показник адіабати), R – універсальна газова стала,  – молярна маса, Т – абсолютна температура.

 Закони зміни з часом заряду на обкладках конденсатора та різниці потенціалів між обкладками в реальному коливальному контурі за формою однакові, адже U та q є прямо пропорційними величинами (, С – електроємність):

,

,

де коефіцієнт згасання коливань , R – активний опір котушки, L – її індуктивність, , , q₀ і U₀ – значення q_max та U_max при t = 0, причому .

Закон зміни сили струму запишемо лише для ідеального контура (R = 0):

,

. Період коливань в такому контурі

.

• Період електромагнітних коливань в реальному контурі

.

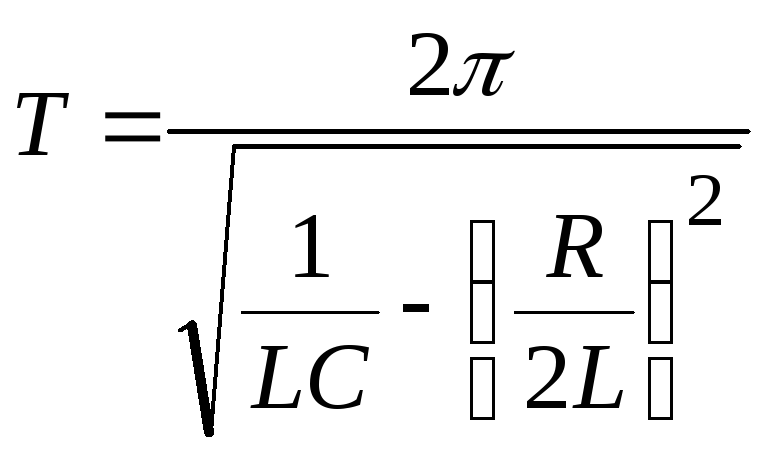• У випадку вимушених електромагнітних коливань резонанс напруг наступає, якщо циклічна частота зовнішньої періодичної напруги наближається до резонансної частоти контура 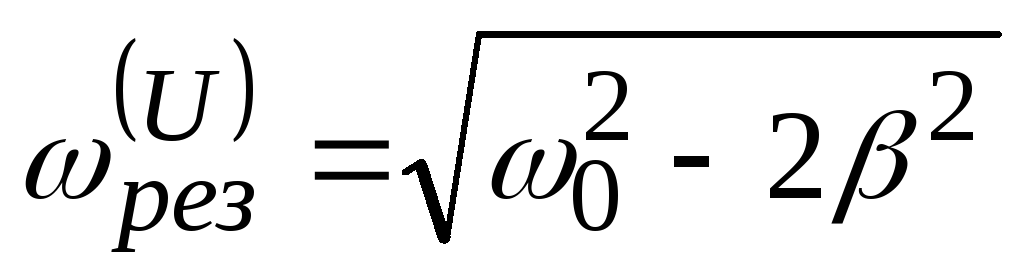, а резонанс струмів при .

 Рівняння плоскої електромагнітної хвилі, що поширюється вздовж осі Ох

де: та – напруженості електричного і магнітного полів хвилі, та – амплітуди відповідних величин.

 Зв’язок модулів напруженостей E і H

,

де: та – електрична і магнітна сталі;  та  – діелектрична і магнітна проникності середовища.

 Модуль швидкості поширення електромагнітних хвиль

,

– електродинамічна стала. Оскільки v залежить від середовища, то й довжина хвилі різна в різних середовищах (період коливань і, відповідно, частота незмінні).

 Інтенсивність електромагнітної хвилі

.