
- •1. Основні закони і співвідношення
- •2. Приклади розв’язування задач
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •3. Задачі для самостійного розв’язування
- •3.1. Поле прямолінійного й колового провідника зі струмом, соленоїда
- •3.2. Сила Лоренца
- •3.3. Закони Ампера, соленоїд, контур зі струмом у магнітному полі, магнітний потік, явище електромагнітної індукції, індуктивність, енергія магнітного поля
- •1. Основні закони і співвідношення
- •2. Приклади розв’язування задач
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •3. Задачі для самостійного розв’язування
- •3.1. Механічні коливання і хвилі
- •3.2. Електромагнітні коливання і хвилі
- •1. Основні закони і співвідношення
- •2. Приклади розв’язування задач
- •Розв’язання
- •Р озв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання.
- •3. Задачі для самостійного розв’язування
- •3.1. Геометрична і хвильова оптика
- •3.2. Квантова оптика
- •1. Основні закони і співвідношення
- •1.1. Воднеподібні атоми в теорії Бора. Гіпотеза де Бройля. Співвідношення невизначеностей
- •1.2. Хвильові властивості мікрочастинок
- •1.3. Рівняння Шрьодінгера і його розв’язки
- •2. Приклади розв’язування задач
- •Розв'язання
- •Розв'язання
- •Розв'язання
- •Розв'язання
- •Розв'язання
- •Розв’язання
- •Розв'язання
- •Розв'язання
- •Розв'язання
- •Розв'язання
- •3. Задачі для самостійного розв’язування
- •1. Основні закони і співвідношення
- •1.1. Будова ядра, енергія зв'язку
- •1.2. Радіоактивність
- •1.3. Ядерні реакції
- •2. Приклади розв'язування задач
- •Розв'язання
- •Розв'язування
- •Розв'язання
- •3. Задачі для самостійного розв’язування
Розв'язання
|
Дано:
|
|
|
![]() .
.
На основі законів
збереження зарядового і масового чисел
одержуємо: 2+7=1+Z
і 4+14=1+А. Це дає: Z=8,
A=17;
значить, виникає ядро ізотопу кисню
![]() ,
тому остаточно, реакція набуває вигляду:
,
тому остаточно, реакція набуває вигляду:
![]() .
.
Енергія реакції Q визначається через дефект маси реакції:
![]() .
.
Підставляючи числові дані, одержуємо:
![]() ;
;
знак (-) означає, що енергія в цій реакції поглинається.
Г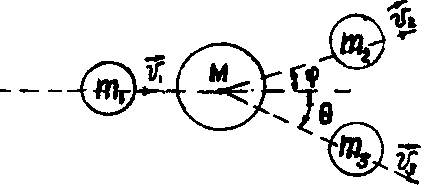 рафічно
розглядувану реакцію можна зобразити
на малюнку:
рафічно
розглядувану реакцію можна зобразити
на малюнку:
Тут
![]() ,
,
![]() ,
,
![]() – маси
-частинки,
ядра азоту, протона і ядра кисню (наближено
будемо користуватися масовими числами);
ядро азоту вважається нерухомим,
– маси
-частинки,
ядра азоту, протона і ядра кисню (наближено
будемо користуватися масовими числами);
ядро азоту вважається нерухомим,
![]() ,
,
![]() ,
,
![]() – швидкості відповідних частинок,
– швидкості відповідних частинок,
![]() ,
,
![]() ,
,
![]() – їх імпульси,
– їх імпульси,
![]() ,
,
![]() ,
,
![]() – кінетичні
енергії. Легко переконатися, що енергії
розглядуваних частинок значно менші
від їх енергій спокою, тому можна
користуватися формулами класичної
механіки. На основі законів збереження
енергії та імпульсу одержуємо:
– кінетичні
енергії. Легко переконатися, що енергії
розглядуваних частинок значно менші
від їх енергій спокою, тому можна
користуватися формулами класичної
механіки. На основі законів збереження
енергії та імпульсу одержуємо:
![]() ,
(3.1)
,
(3.1)
![]() .
(3.2)
.
(3.2)
За теоремою косинусів
![]() .
(3.3)
.
(3.3)
Оскільки
![]() ,
де
,
де
![]() ,
то
,
то
![]() . (3.4)
. (3.4)
Тому рівняння (3.3) набуває вигляду
![]() .
(3.5)
.
(3.5)
Виключаючи з (3.1) і (3.5) енергію Е3, одержуємо
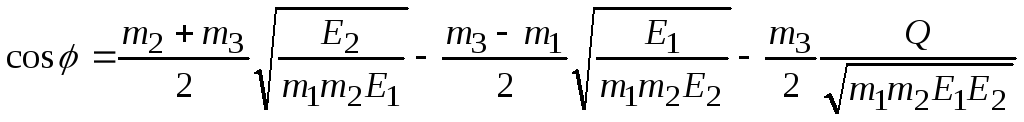 (3.6)
(3.6)
Підставивши числові значення в рівняння (3.6), отримаємо
![]()
і
![]() .
Таким чином, протон і ядро віддачі
продовжують рухатися в напрямку падаючої
-частинки.
.
Таким чином, протон і ядро віддачі
продовжують рухатися в напрямку падаючої
-частинки.
Відповідь: Z = 8, A = 17, Q = -1,2 МеВ, = 0.
3. Задачі для самостійного розв’язування
-
Знайти питому енергію зв'язку ядер:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)![]() ;
д)
;
д)
![]() .
.
-
Який ізотоп утворюється з
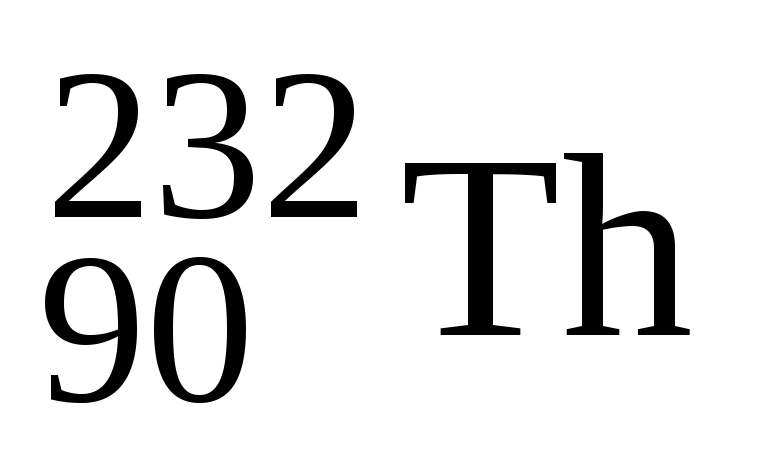 після чотирьох -розпадів
та двох
після чотирьох -розпадів
та двох
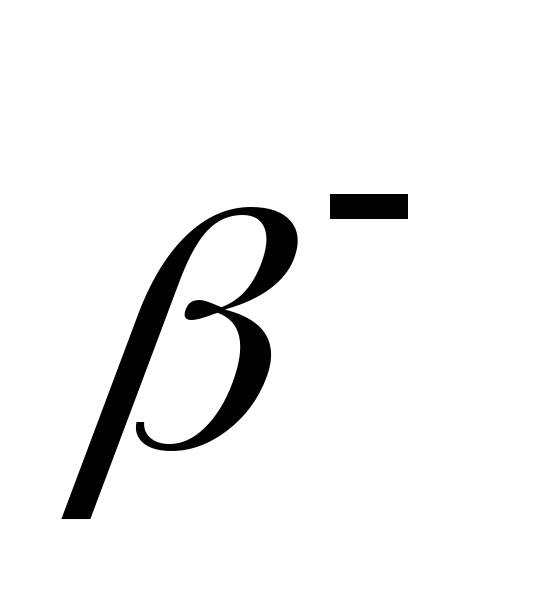 -розпадів?
-розпадів? -
Який ізотоп утворюється з
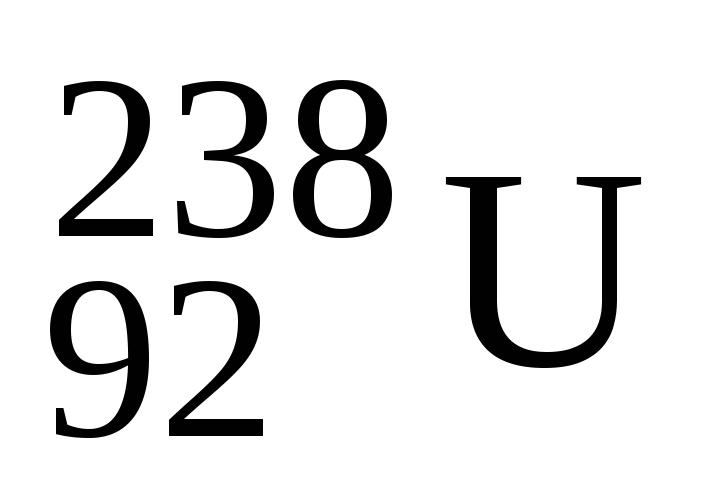 після трьох -розпадів
та двох
після трьох -розпадів
та двох
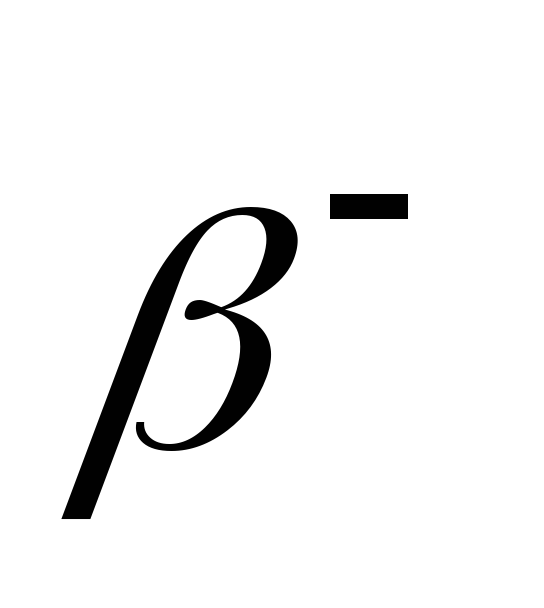 -розпадів?
-розпадів? -
Який ізотоп утворюється з
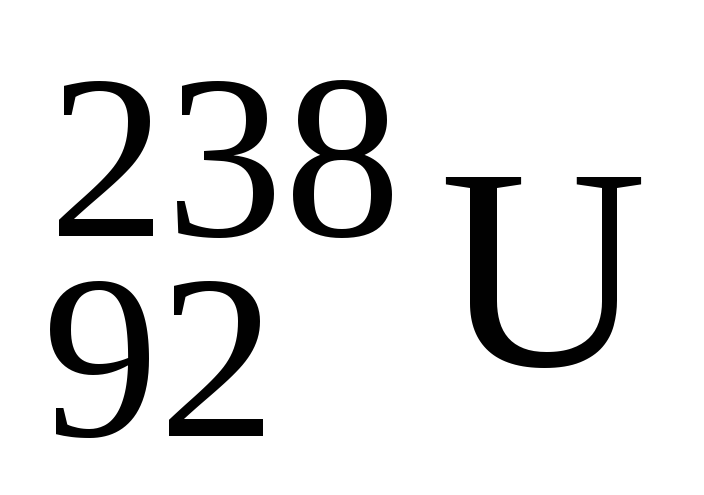 після двох
після двох
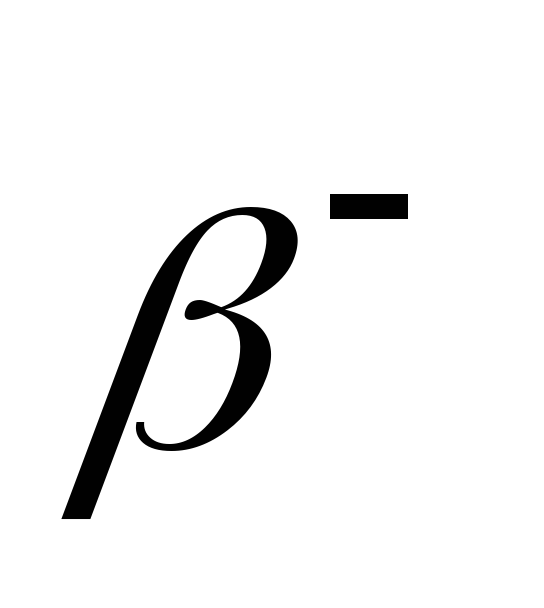 -розпадів
та одного -розпаду?
-розпадів
та одного -розпаду? -
Деякий радіоактивний ізотоп має постійну розпаду
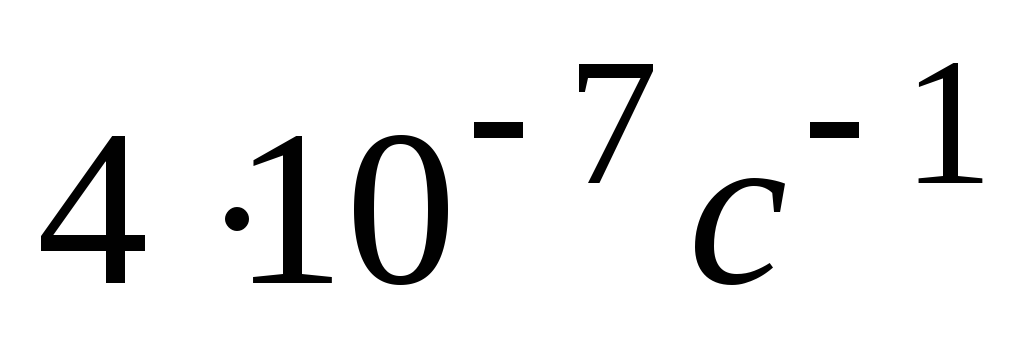 .
Через який проміжок часу розпадеться
75% від початкової кількості атомів?
.
Через який проміжок часу розпадеться
75% від початкової кількості атомів? -
Скільки атомів радону розпадається за одну добу з числа
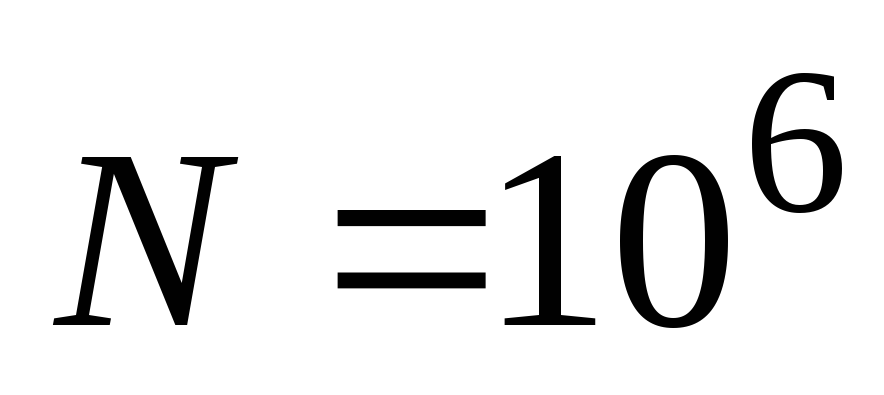 атомів?
атомів? -
Знайти масу радону, активність якого
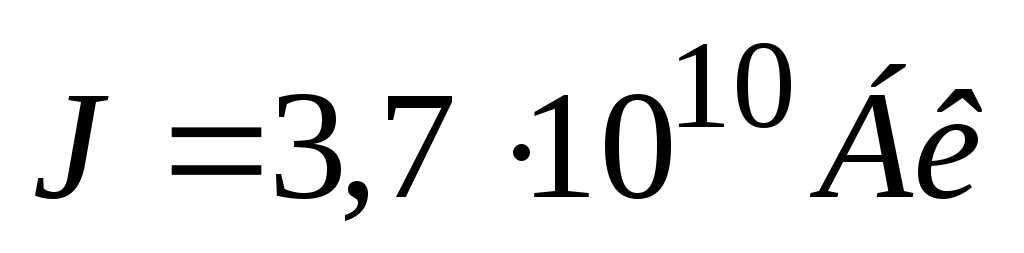 .
. -
Знайти масу полонію
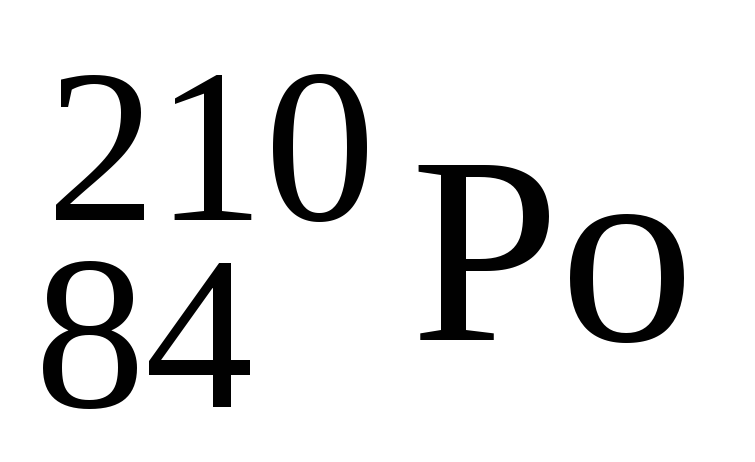 ,
активність якого
,
активність якого
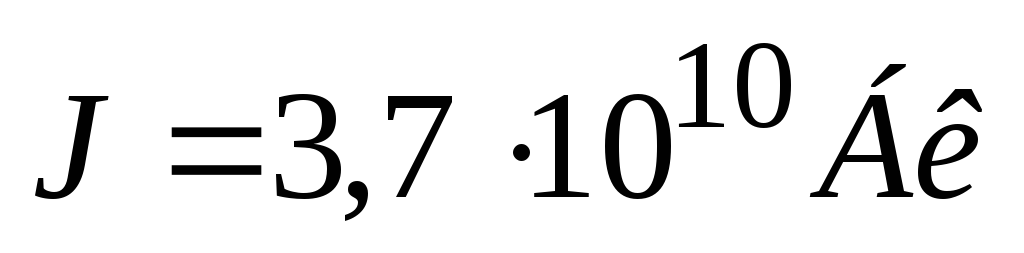 .
. -
Знайти постійну розпаду радону, якщо відомо, що число атомів радону зменшується за 1 добу на 18,2%.
-
Знайти активність 1мкг полонію.
-
Дописати позначення, яких не вистачає в реакціях:
а)
![]() ; б)
; б)
![]() ;
;
в)![]() ; г)
; г)
![]() .
.
-
Розрахувати енергетичний ефект реакцій:
а)
![]() ; б)
; б)
![]() ;
;
в)![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() .
.
-
При бомбардуванні ізотопу азоту
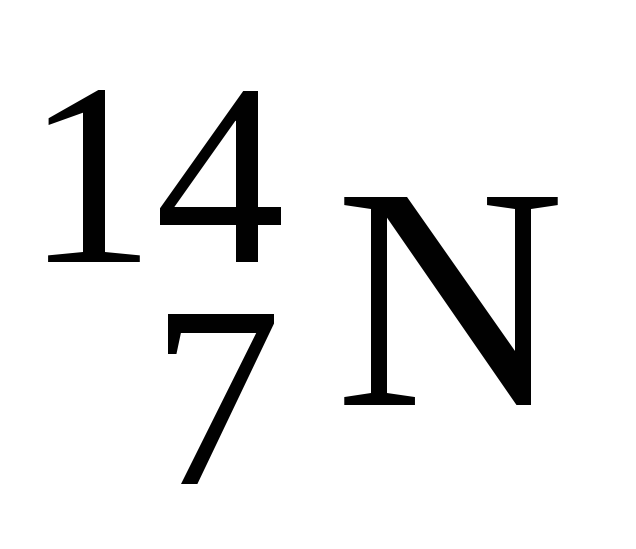 нейтронами одержується ізотоп вуглецю
нейтронами одержується ізотоп вуглецю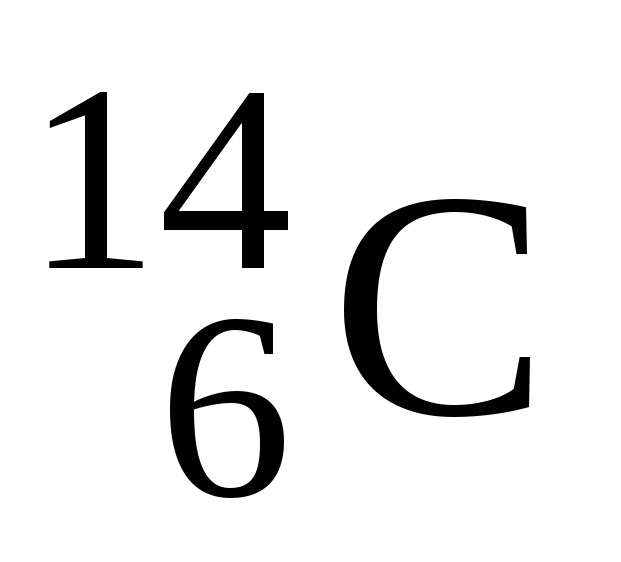 ,
що виявляється
,
що виявляється
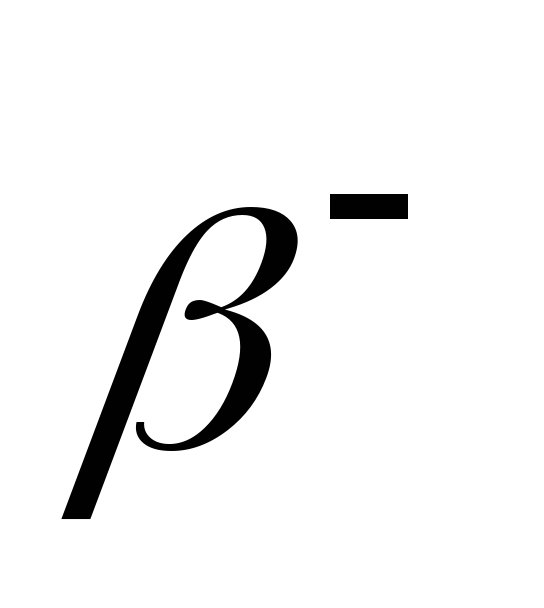 -радіоактивним.
Записати рівняння обох реакцій.
-радіоактивним.
Записати рівняння обох реакцій. -
При бомбардуванні ізотопу літію
 дейтонами
дейтонами
 виникають дві -частинки.
При цьому виділяється енергія
виникають дві -частинки.
При цьому виділяється енергія
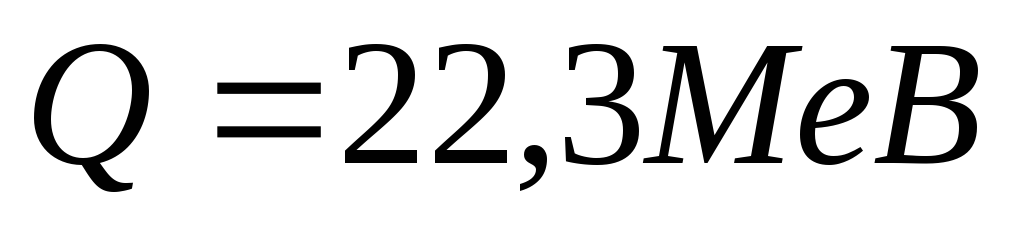 .
Знаючи маси дейтона і -частинки,
знайти масу ізотопу літію
.
Знаючи маси дейтона і -частинки,
знайти масу ізотопу літію
 .
. -
Штучний ізотоп азоту
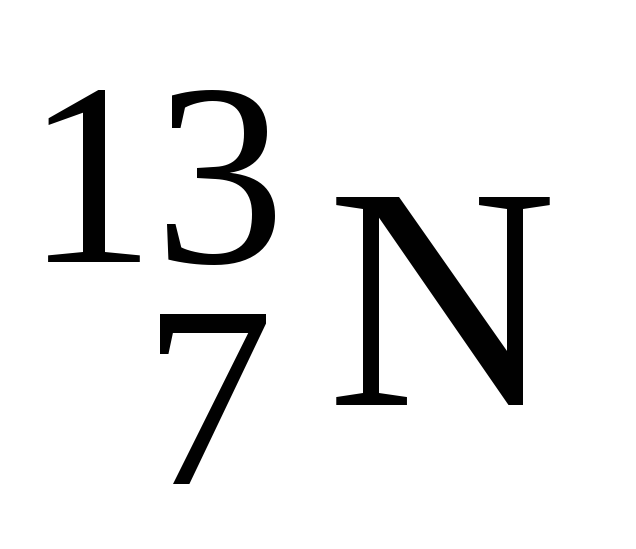 одержується бомбардуванням ядер вуглецю
одержується бомбардуванням ядер вуглецю
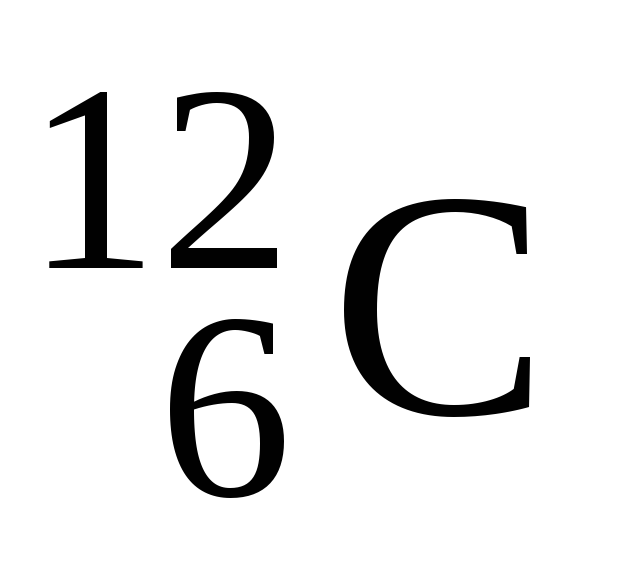 дейтонами. Записати рівняння реакції.
Знайти кількість теплоти, поглинуту
при цій реакції.
дейтонами. Записати рівняння реакції.
Знайти кількість теплоти, поглинуту
при цій реакції. -
Реакція
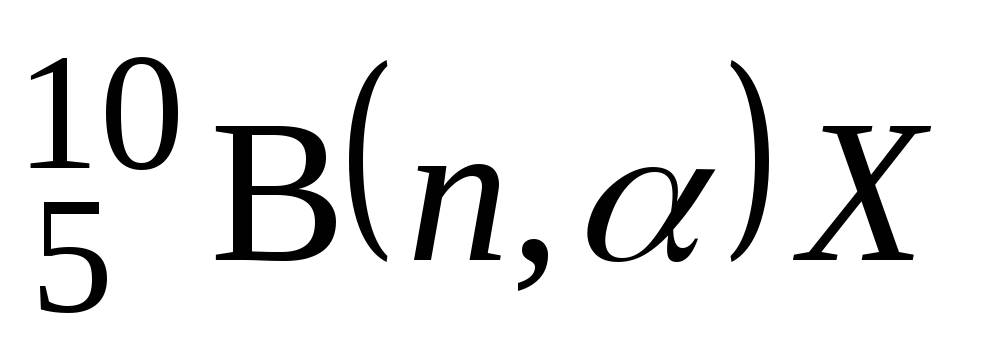 йде при бомбардуванні бору тепловими
нейтронами. Записати рівняння реакції.
Яка енергія виділяється при цій реакції?
йде при бомбардуванні бору тепловими
нейтронами. Записати рівняння реакції.
Яка енергія виділяється при цій реакції? -
При бомбардуванні ізотопу літію
 дейтонами утворюються дві -частинки,
які розлітаються симетрично під кутом
до напрямку швидкості бомбардуючих
дейтонів. Яку кінетичну енергію мають
-частинки,
якщо енергія бомбардуючих дейтонів
0,2 МеВ? Знайти кут .
дейтонами утворюються дві -частинки,
які розлітаються симетрично під кутом
до напрямку швидкості бомбардуючих
дейтонів. Яку кінетичну енергію мають
-частинки,
якщо енергія бомбардуючих дейтонів
0,2 МеВ? Знайти кут . -
При бомбардуванні ізотопу літію
 протонами утворюються дві -частинки.
Кінетична енергія кожної -частинки
в момент їх виникнення 9,15МеВ. Яка енергія
протонів?
протонами утворюються дві -частинки.
Кінетична енергія кожної -частинки
в момент їх виникнення 9,15МеВ. Яка енергія
протонів? -
Яку енергію (в кіловат-годинах) можна одержати від поділу одного грама урану
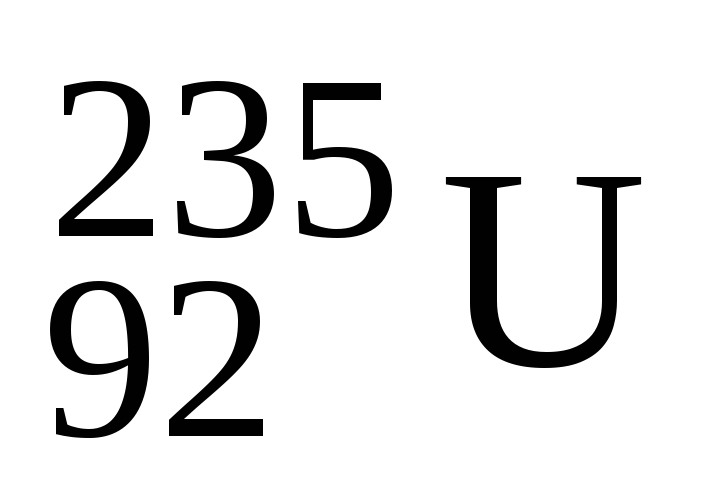 ,
якщо при кожному акті ділення ядра
виділяється енергія 200МеВ?
,
якщо при кожному акті ділення ядра
виділяється енергія 200МеВ? -
Яка маса урану
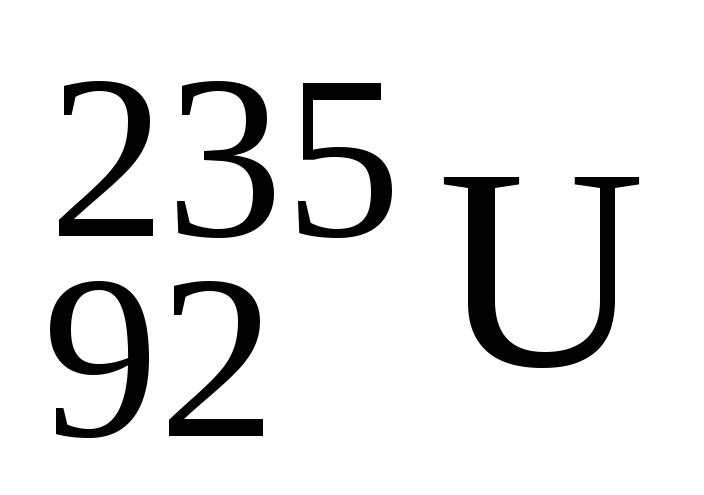 витрачається за одну добу на атомній
електростанції потужністю 5000кВт? ККД
вважати рівним 17%. При кожному акті
ділення ядра виділяється енергія
200МеВ.
витрачається за одну добу на атомній
електростанції потужністю 5000кВт? ККД
вважати рівним 17%. При кожному акті
ділення ядра виділяється енергія
200МеВ. -
При вибуху водневої бомби протікає термоядерна реакція утворення гелію з дейтерію і тритію. Написати рівняння реакції. Знайти енергію, що виділяється при цій реакції. Скільки енергії можна одержати при утворенні одного грама гелію?
-
Знайти найменшу енергію -кванта, достатню для розкладу дейтона -променями:
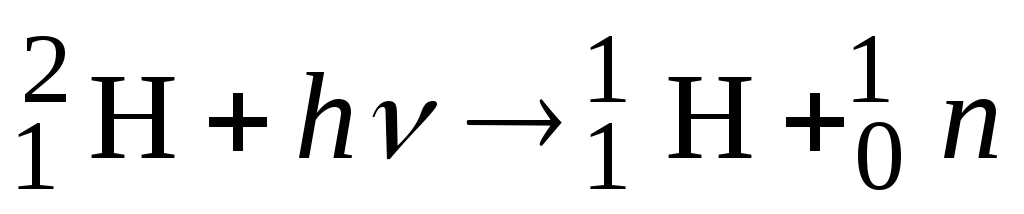 .
. -
Позитрон і електрон об'єднуються, утворюючи два фотони. Знайти енергію кожного з фотонів, вважаючи початкову енергію часток зникаюче малою. Яка довжина хвилі цих фотонів?
-
Електрон і позитрон утворюються фотоном з енергією 2,62МеВ. Яка була повна кінетична енергія позитрона і електрона в момент виникнення?
-
Нерухомий нейтральний -мезон перетворюється у два фотони. Знайти енергію кожного фотона. Маса -мезона
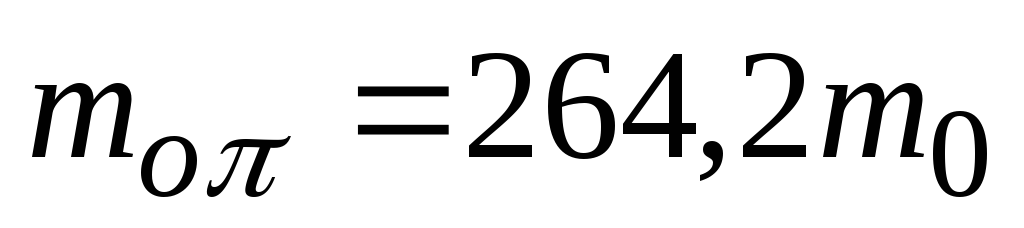 ,
де
,
де
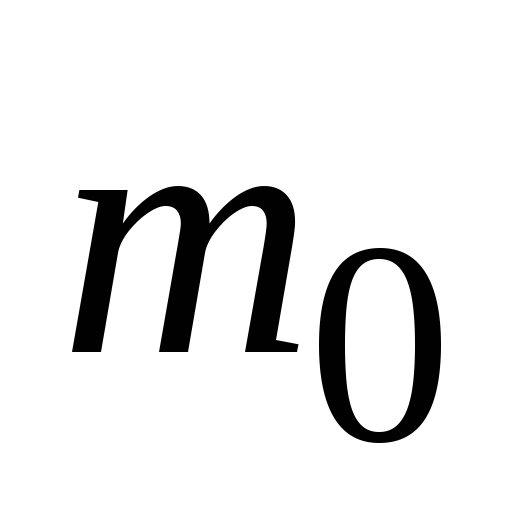 – маса
електрона.
– маса
електрона. -
Нейтрон і антинейтрон об'єднуються, утворюючи два фотони. Знайти енергію кожного з фотонів, вважаючи початкову енергію частинок безмежно малою.
