3. Сходимость по вероятности

Сходимость относительной частоты к вероятности р отличается от сходимости в смысле математического анализа. Для того чтобы подчеркнуть это различие, вводят понятие «сходимость по вероятности».

Различие между указанными видами сходимости состоит в следующем: если стремится при n → ∞ к р как пределу в смысле математического анализа, то начиная с некоторого n = n₀ и для всех последующих значений (n > n₀) неуклонно выполняется неравенство < ε (ε > 0) (рис. 3.1), если же стремится по вероятности к р при n → ∞, то для отдельных значений из n > n₀ неравенство может не выполняться (рис. 3.2). Коротко это можно записать так: р.

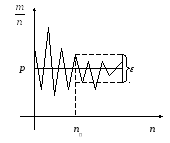
Рис. 3.1 Рис. 3.2

4. Закон больших чисел в формАх Чебышева, Бернулли. Теорема Пуассона

4.1. Закон больших чисел в форме Чебышева

Если явление устойчивости средних имеет место в действительности, то в математической модели, с помощью которой мы изучаем случайные явления, должна существовать отражающая этот факт теорема. В условиях этой теоремы введем ограничения на случайные величины X₁, X₂, …, X_n:

а) каждая случайная величина Х_i имеет математическое ожидание

M(Х_i) = a;

б) дисперсия каждой случайной величины конечна или, можно сказать, что дисперсии ограничены сверху одним и тем же числом, например С, т. е.

D(Х_i) < C, i = 1, 2, …, n;

в) случайные величины попарно независимы, т. е. любые две X_i и X_j при i  j независимы.

Тогда, очевидно

D(X₁ + X₂ + … + X_n)  D(X₁) + D(X₂) + ... + D(X_n).

Сформулируем закон больших чисел в форме Чебышева.

Теорема Чебышева: при неограниченном увеличении числа n независимых испытаний «средняя арифметическая наблюдаемых значений случайной величины сходится по вероятности к ее математическому ожиданию», т. е. для любого положительного ε

Р(|– а| < ε) = 1. (4.1.1)

Смысл выражения «средняя арифметическая = сходится по вероятности к a» состоит в том, что вероятность того, что будет сколь угодно мало отличаться от a, неограниченно приближается к 1 с ростом числа n.

Доказательство. Для конечного числа n независимых испытаний применим неравенство Чебышева для случайной величины = :

Р(|– M()| < ε) ≥ 1 – . (4.1.2)

Учитывая ограничения а – в, вычислим M() и D():

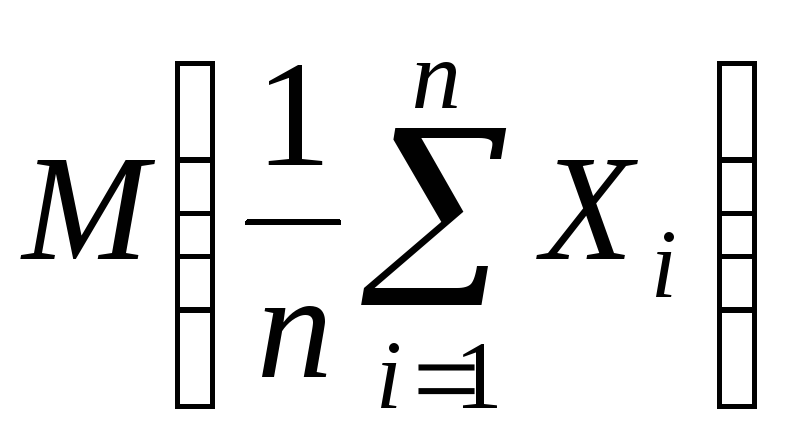M() = = = = = = а;

D() = = = = = = .

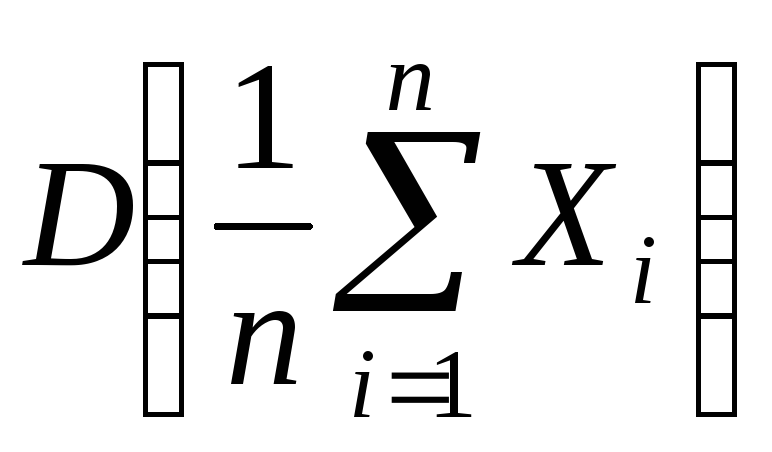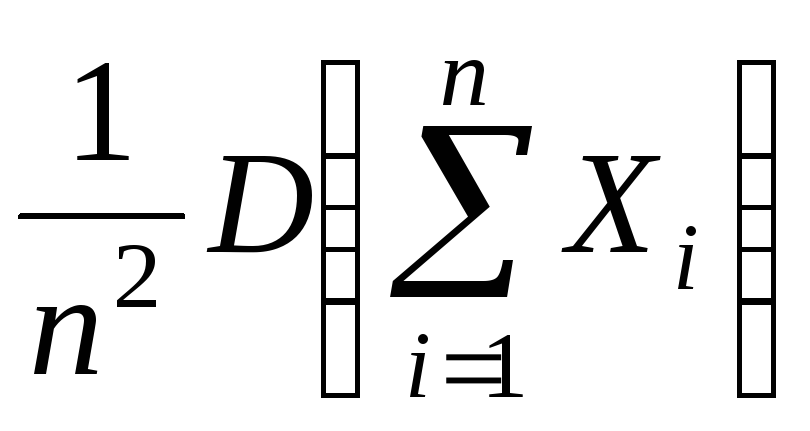Подставляя M() и D() в неравенство (4.1.2), получим

Р(|– а| < ε) ≥ 1 – .

Если в неравенстве (4.1.2) взять сколь угодно малое ε > 0 и n  , то получим

= 1,

что и доказывает теорему Чебышева.

Из рассмотренной теоремы вытекает важный практический вывод: неизвестное нам значение математического ожидания случайной величины мы вправе заменить средним арифметическим значением, полученным по достаточно большому числу опытов. При этом, чем больше опытов для вычисления, тем с большей вероятностью (надежностью) можно ожидать, что связанная с этой заменой ошибка (– а) не превзойдет заданную величину ε.

Кроме того, можно решать другие практические задачи. Например, по значениям вероятности (надежности) Р = Р(|– а| < ε) и максимальной допустимой ошибке ε определить необходимое число опытов n; по Р и п определить ε; по ε и п определить границу вероятности события |– а | < ε.

Частный случай. Пусть при n испытаниях наблюдаются n значений случайной величины X, имеющей математическое ожидание M(X) и дисперсию D(X). Полученные значения можно рассматривать как случайные величины Х₁, Х₂, Х₃, ..., Х_n,. Это следует понимать так: серия из п испытаний проводится неоднократно, поэтому в результате i-го испытания, i = l, 2, 3, ..., п, в каждой серии испытаний появится то или иное значение случайной величины X, не известное заранее. Следовательно, i-e значение x_i случайной величины, полученное в i-м испытании, изменяется случайным образом, если переходить от одной серии испытаний к другой. Таким образом, каждое значение x_i можно считать случайной величиной X_i .

Предположим, что испытания удовлетворяют следующим требованиям:

1. Испытания независимы. Это означает, что результаты Х₁, Х₂, Х₃, ..., Х_n испытаний – независимые случайные величины.

2. Испытания проводятся в одинаковых условиях – это означает, с точки зрения теории вероятностей, что каждая из случайных величин Х₁, Х₂, Х₃, ..., Х_n имеет такой же закон распределения, что и исходная величина X, поэтому M(X_i) = M(X) и D(X_i) = D(X), i = 1, 2, .... п.

Учитывая вышеуказанные условия, получим

Р(|– а| < ε) ≥ 1 – . (4.1.3)

Пример 4.1.1. Дисперсия случайной величины X равна 4. Сколько требуется произвести независимых опытов, чтобы с вероятностью не менее 0,9 можно было ожидать, что среднее арифметическое значение этой случайной величины будет отличаться от математического ожидания менее чем на 0,5?

Решение. По условию задачи ε = 0,5; Р(|– а|< 0,5) ≥ 0,9. Применив формулу (4.1.3) для случайной величины Х, получим

P(|– M(X)| < ε) ≥ 1 – .

Из соотношения

1 – = 0,9

определим

= 0,1;

п = = = 160.

Ответ: требуется произвести 160 независимых опытов.

Если предположить, что средняя арифметическая распределена нормально, то получаем:

Р(|– а| < ε)= 2Φ() ≥ 0,9.

Откуда, воспользовавшись таблицей функции Лапласа, получим ≥ ≥ 1,645, или ≥ 6,58, т. е. n ≥ 49.

Пример 4.1.2. Дисперсия случайной величины Х равна D(Х) = 5. Произведено 100 независимых опытов, по которым вычислено . Вместо неизвестного значения математического ожидания а принята . Определить максимальную величину ошибки, допускаемую при этом с вероятностью не менее 0,8.

Решение. По условию задачи n = 100, Р(| – а| < ε) ≥ 0,8. Применим формулу (4.1.3)

Р(| – а| < ε) ≥ 1 – .

Из соотношения

1 – = 0,8

определим ε:

= 0,2;

ε² = = = 0,25.

Следовательно, ε = 0,5.

Ответ: максимальная величина ошибки ε = 0,5.