- •Высшая математика
- •Непрерывность функции
- •Функции нескольких переменных
- •Учебно-методическое пособие
- •Лекция 1. Непрерывность функции
- •Непрерывность функции в точке. Свойства функций, непрерывных в точке
- •Точки разрыва функции и их классификация
- •Непрерывность функции
- •Лекция 2. Функции нескольких переменных
- •Понятие функции двух и более переменных
- •Предел и непрерывность функции двух переменных
- •Частные производные первого порядка. Полный дифференциал
- •Частные производные высших порядков
- •Экстремум функции нескольких переменных. Необходимые и достаточные условия существования экстремума
- •Условный экстремум
- •Функции нескольких переменных
- •Литература
- •Ответы к задачам и упражнениям Непрерывность функции
- •Функции нескольких переменных
- •Содержание
- •1. Непрерывность функции в точке. Свойства функций, непрерывных в точке 3
- •220086, Г. Минск, ул. Славинского, 1, корп. 3.
-
Точки разрыва функции и их классификация
Точки, в которых
условие непрерывности не выполняется,
называются точками разрыва этой функции.
Если
![]() – точка разрыва функции
– точка разрыва функции
![]() ,
то в ней не выполняется хотя бы одно из
трех условий непрерывности функции,
указанных в определениях 1, 2, а именно:
,
то в ней не выполняется хотя бы одно из
трех условий непрерывности функции,
указанных в определениях 1, 2, а именно:
-
Функция определена в окрестности точки
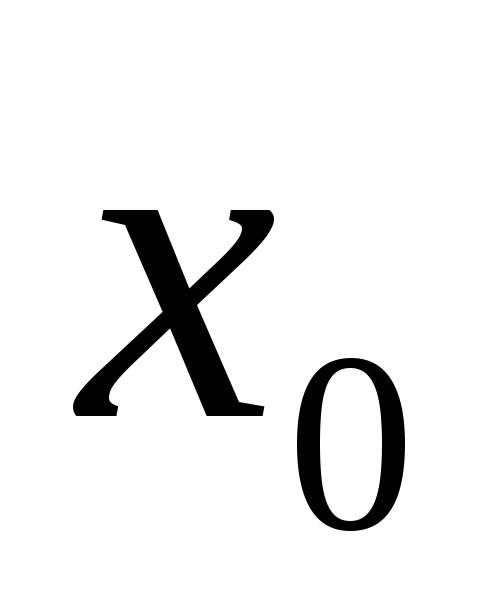 ,
но не определена в самой точке
,
но не определена в самой точке
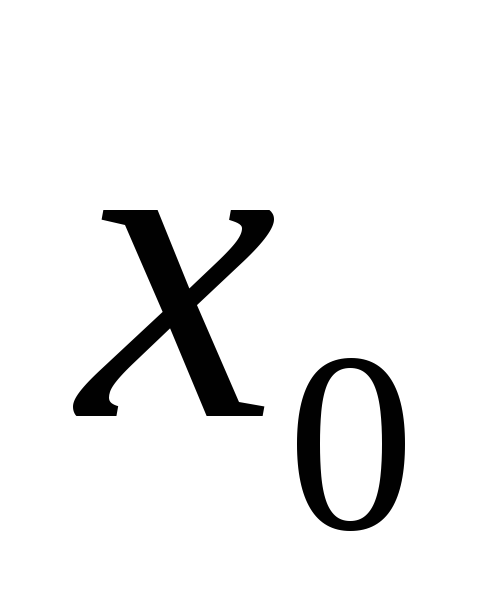 .
Так функция
.
Так функция
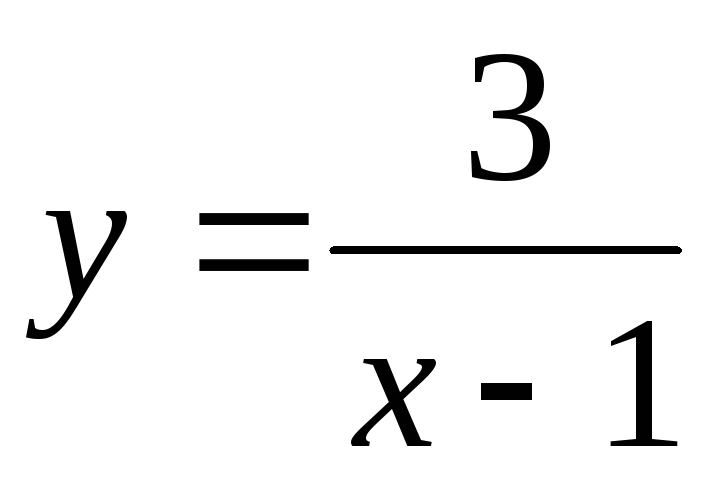 ,
рассмотренная в примере 2 а) имеет разрыв
в точке
,
рассмотренная в примере 2 а) имеет разрыв
в точке
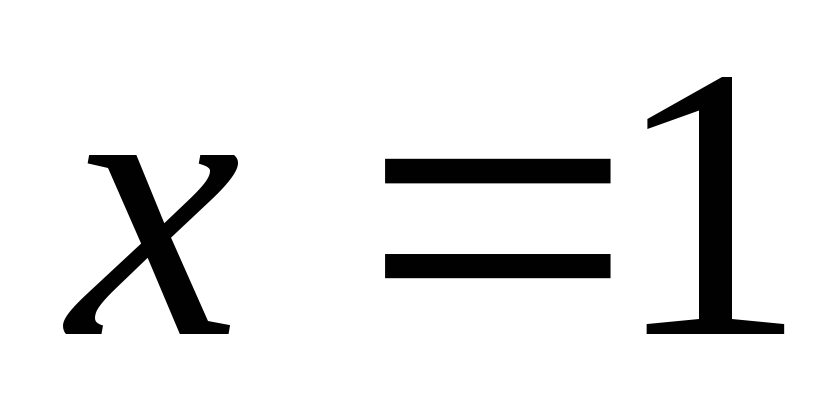 ,
так как не определена в этой точке.
,
так как не определена в этой точке. -
Функция определена в точке
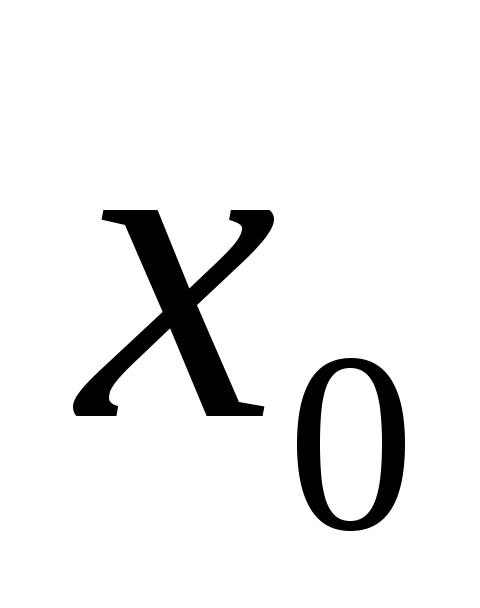 и ее окрестности, существуют односторонние
пределы
и ее окрестности, существуют односторонние
пределы
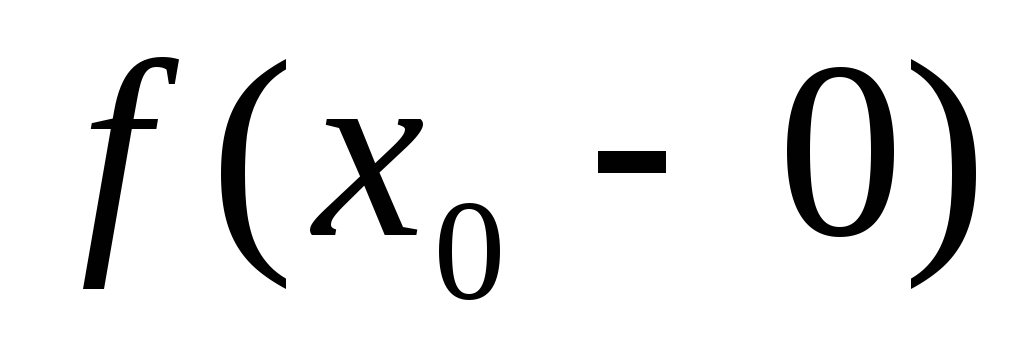 и
и
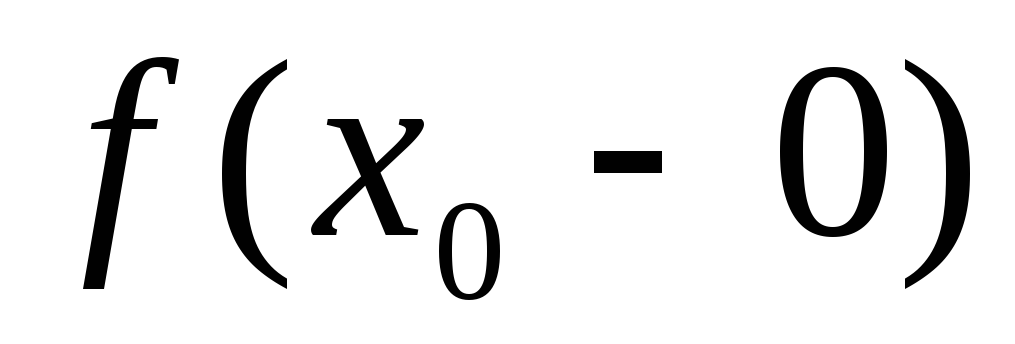 ,
но они не равны между собой:
,
но они не равны между собой:
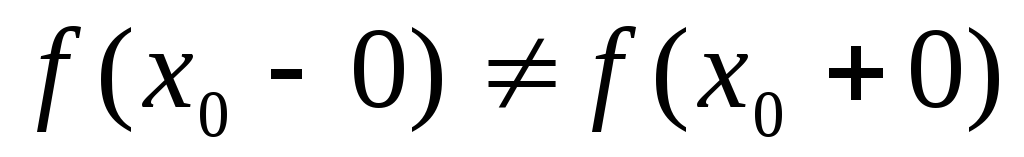 .
Например, функция
.
Например, функция
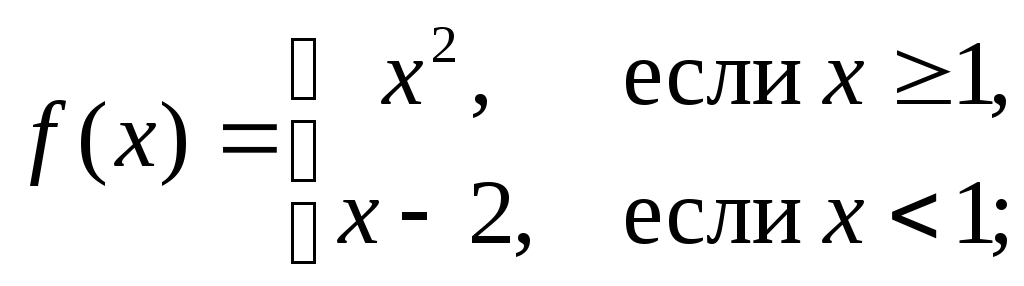 из примера 2 б) определена в точке
из примера 2 б) определена в точке
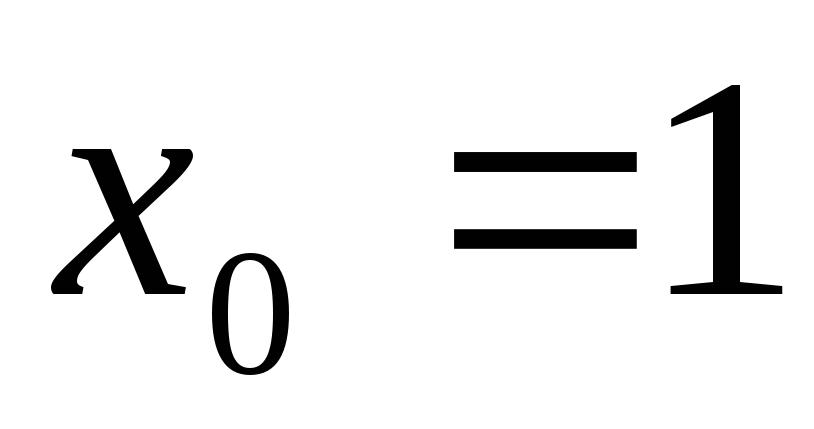 и ее окрестности, но
и ее окрестности, но
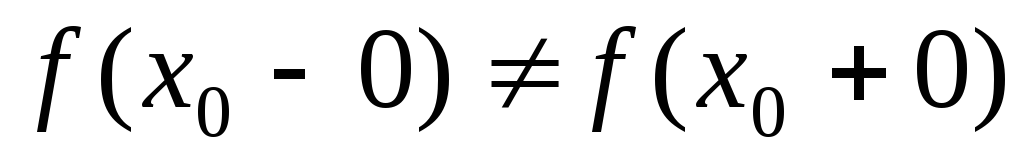 ,
так как
,
так как
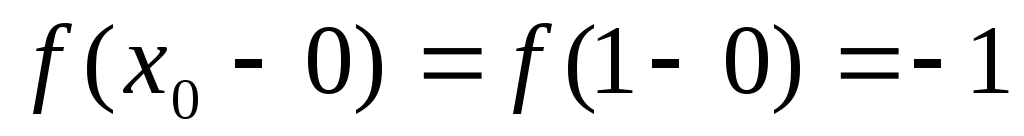 ,
а
,
а
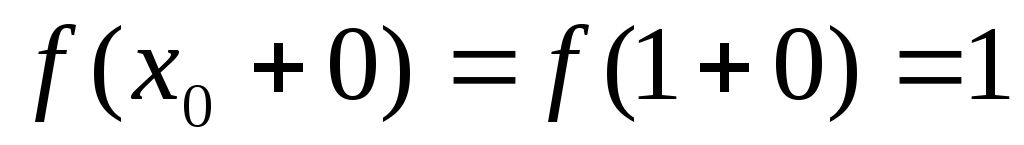 .
. -
Функция определена в точке
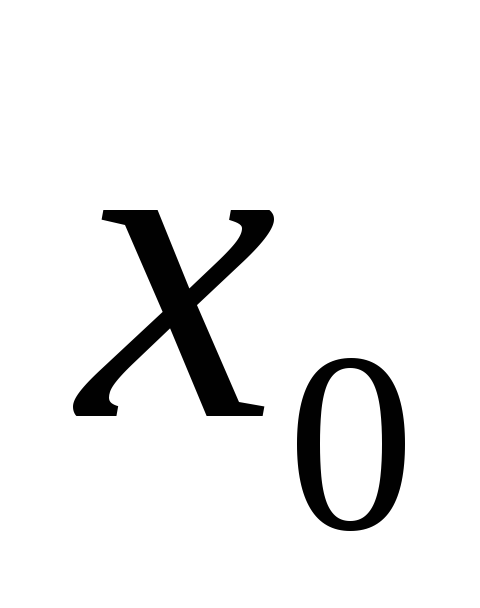 и ее окрестности, существуют односторонние
пределы
и ее окрестности, существуют односторонние
пределы
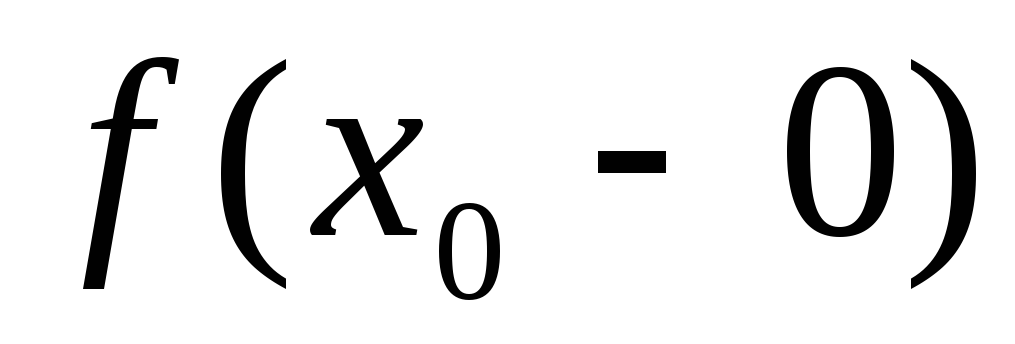 и
и
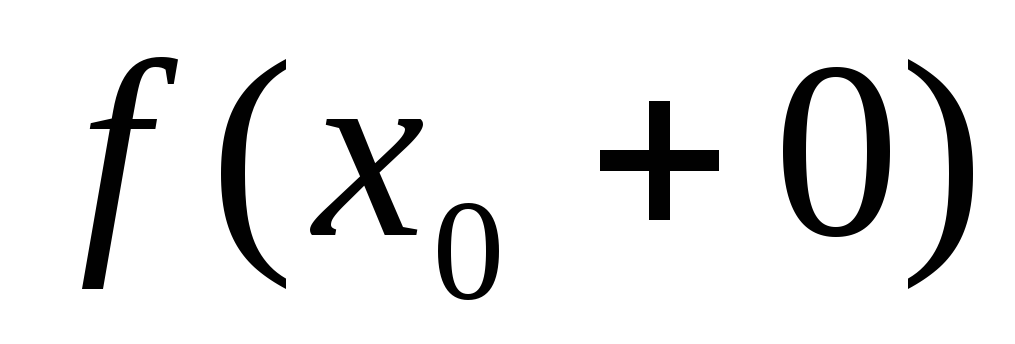 ,
они равны между собой, но не равны
значению функции в точке
,
они равны между собой, но не равны
значению функции в точке
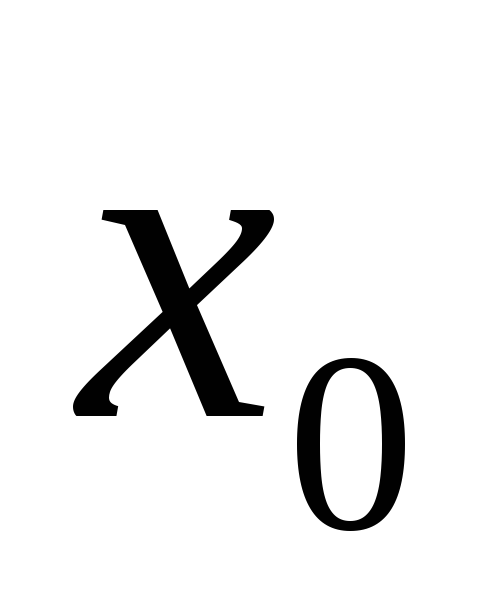 :
:
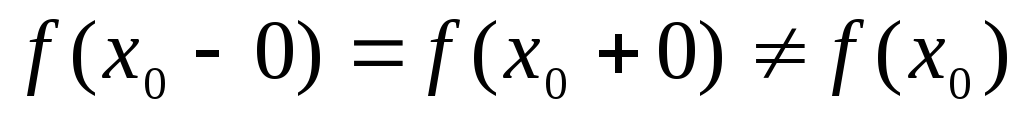 .
Например, функция
.
Например, функция
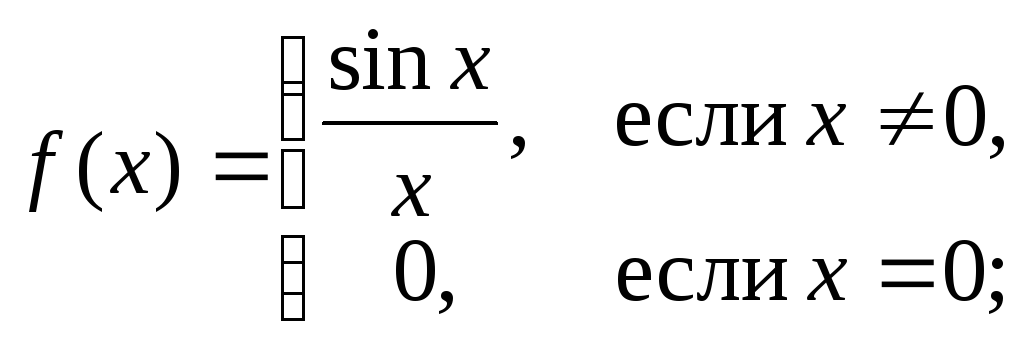 .
Здесь
.
Здесь
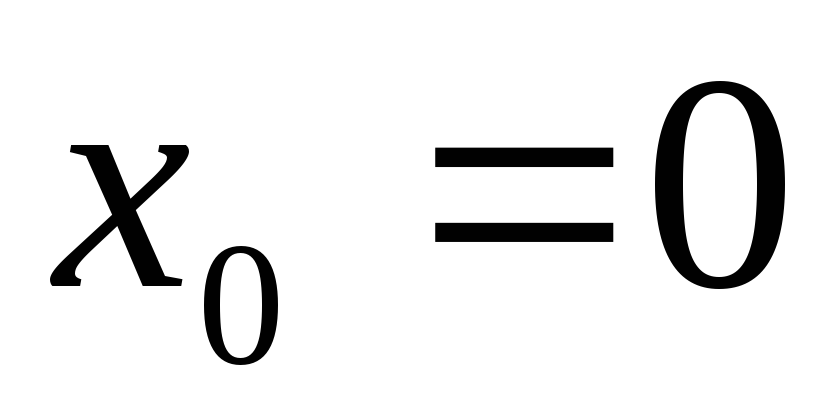 – точка разрыва: в этой точке функция
определена, существуют односторонние
пределы
– точка разрыва: в этой точке функция
определена, существуют односторонние
пределы
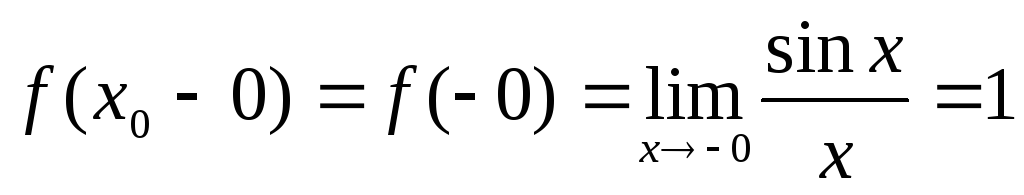 и
и
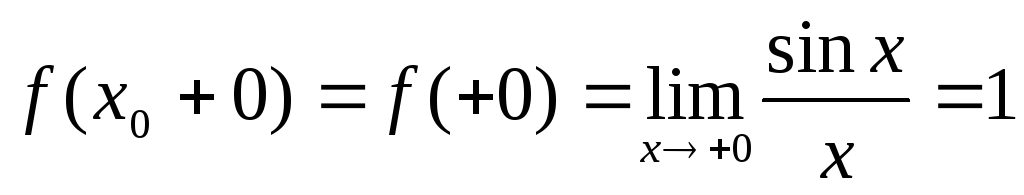 ,
равные между собой, но
,
равные между собой, но
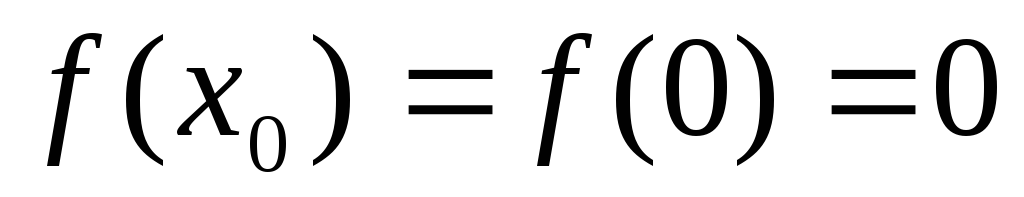 ,
т. е.
,
т. е.
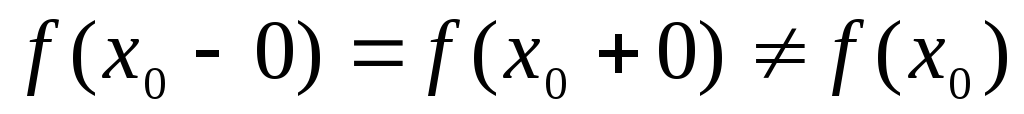 .
.
Точки разрыва функции классифицируются следующим образом.
Определение 5.
Точка
![]() называется точкой
разрыва
первого рода
функции
называется точкой
разрыва
первого рода
функции
![]() ,
если в этой точке существуют конечные
пределы
,
если в этой точке существуют конечные
пределы
![]() и
и
![]() ,
но они не равны между собой:
,
но они не равны между собой:
![]() .
Величина
.
Величина
![]() называется при этом скачком функции
называется при этом скачком функции
![]() в точке
в точке
![]() .
.
Определение 6 .
Точка
![]() называется точкой
устранимого
разрыва
функции
называется точкой
устранимого
разрыва
функции
![]() ,
если в этой точке существуют конечные
пределы
,
если в этой точке существуют конечные
пределы
![]() и
и
![]() ,
они равны между собой:
,
они равны между собой:
![]() ,
но сама функция
,
но сама функция
![]() не определена в точке
не определена в точке
![]() ,
или определена, но
,
или определена, но
![]() .
.
Определение 7.
Точка
![]() называется точкой
разрыва
второго рода
функции
называется точкой
разрыва
второго рода
функции
![]() ,
если в этой точке хотя бы один из
односторонних пределов (
,
если в этой точке хотя бы один из
односторонних пределов (![]() или
или
![]() )
не существует или равен бесконечности.
)
не существует или равен бесконечности.
Пример 3.
Найти точки разрыва следующих функций
и определить их тип: а)
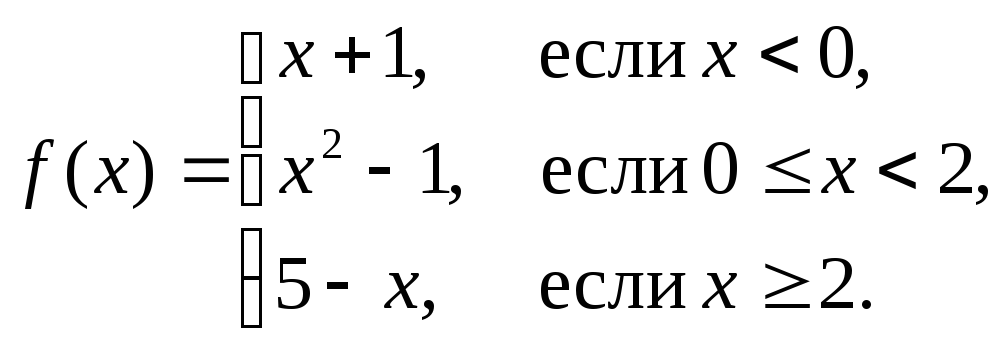 б)
б)
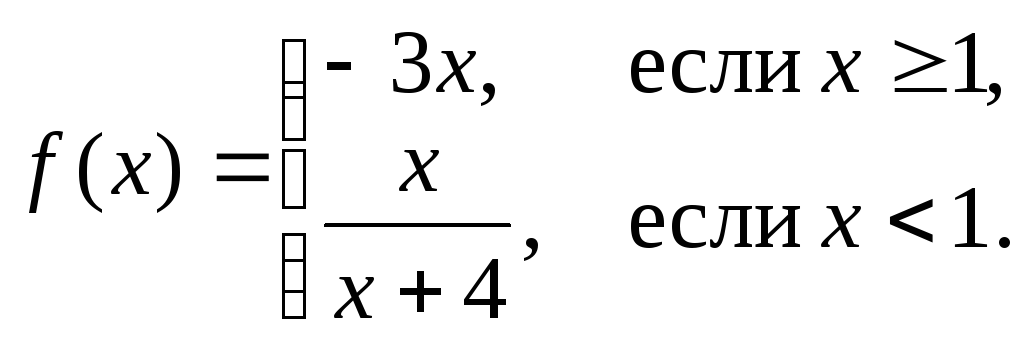
Решение. а)
Функция
![]() определена
и непрерывна на интервалах
определена
и непрерывна на интервалах
![]() ,
,
![]() и
и
![]() ,
так как на каждом из этих интервалов
она задана непрерывными элементарными
функциями. Следовательно, точками
разрыва данной функции могут быть только
те точки, в которых функция меняет свое
аналитическое задание, т.е. точки
,
так как на каждом из этих интервалов
она задана непрерывными элементарными
функциями. Следовательно, точками
разрыва данной функции могут быть только
те точки, в которых функция меняет свое
аналитическое задание, т.е. точки
![]() и
и
![]() .
Найдем односторонние пределы функции
в точке
.
Найдем односторонние пределы функции
в точке
![]() :
:
![]() ,
,
![]() .
.
Так как односторонние
пределы существуют и конечны, но не
равны между собой, то точка
![]() является точкой разрыва первого рода.
Скачок функции:
является точкой разрыва первого рода.
Скачок функции:
![]() .
.
Для точки
![]() находим:
находим:
![]() ,
,
![]() ,
,
![]() .
.
Таким образом,
имеем:
![]() .
Следовательно, в точке
.
Следовательно, в точке
![]() наша функция является непрерывной.
наша функция является непрерывной.
График данной функции изображен на рис.4.
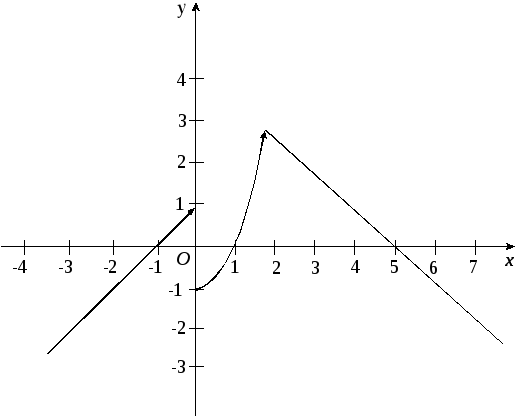
Рис. 4
Решение. б)
В точке
![]() функция меняет свое аналитическое
задание, следовательно, в этой точке
возможен разрыв. Найдем односторонние
пределы:
функция меняет свое аналитическое
задание, следовательно, в этой точке
возможен разрыв. Найдем односторонние
пределы:
![]() ,
,
![]() ,
,
![]() .
.
Так как
![]() ,
то точка
,
то точка
![]() является точкой разры-ва первого рода.
Скачок функции:
является точкой разры-ва первого рода.
Скачок функции:
![]() .
.
В точке
![]() функция не определена, значит точка
функция не определена, значит точка
![]() является точкой разрыва. Определим ее
тип:
является точкой разрыва. Определим ее
тип:
![]() ,
,
![]() .
.
Следовательно, в
точке
![]() функция имеет разрыв второго рода.
функция имеет разрыв второго рода.
ЗАДАЧИ И УПРАЖНЕНИЯ
Непрерывность функции
1. Исследовать следующие функции на непрерывность в указанных точках:
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
д)
![]() е)
е)
![]()
ж)
![]() ;
з)
;
з)
![]() .
.
2. Найти точки разрыва следующих функций и определить их тип:
а)
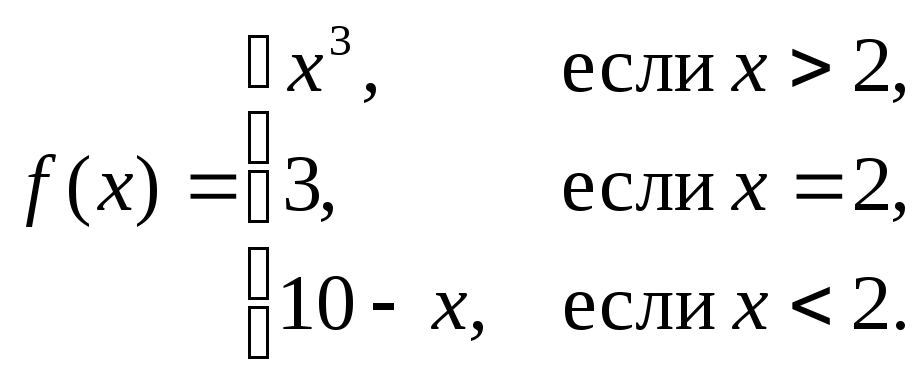 б)
б)
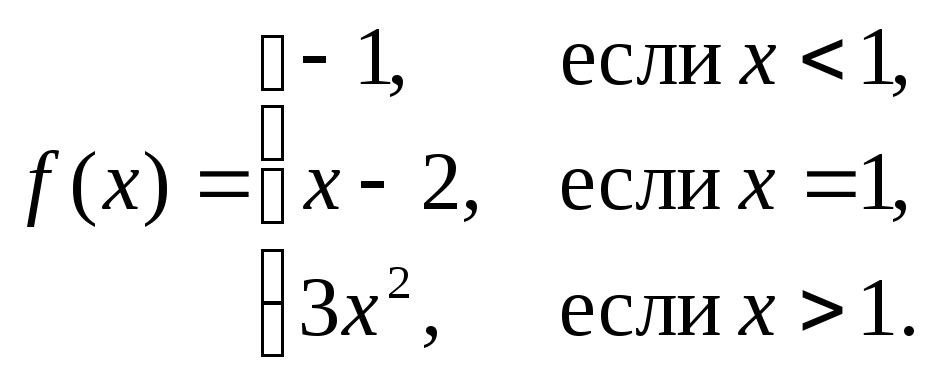
в)
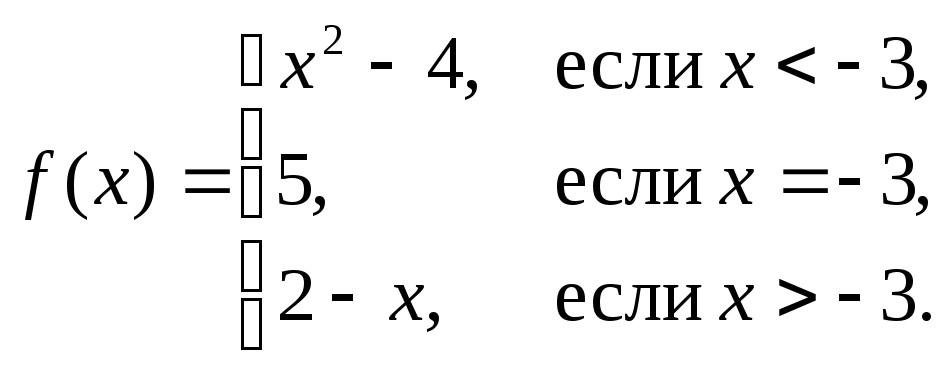 г)
г)
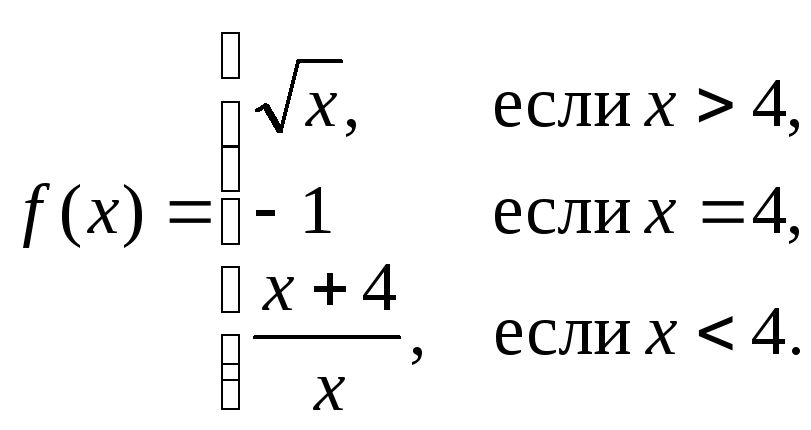
д)
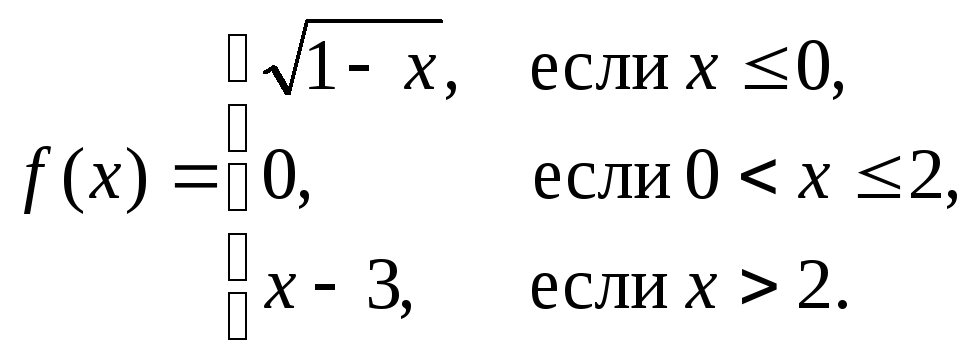 е)
е)
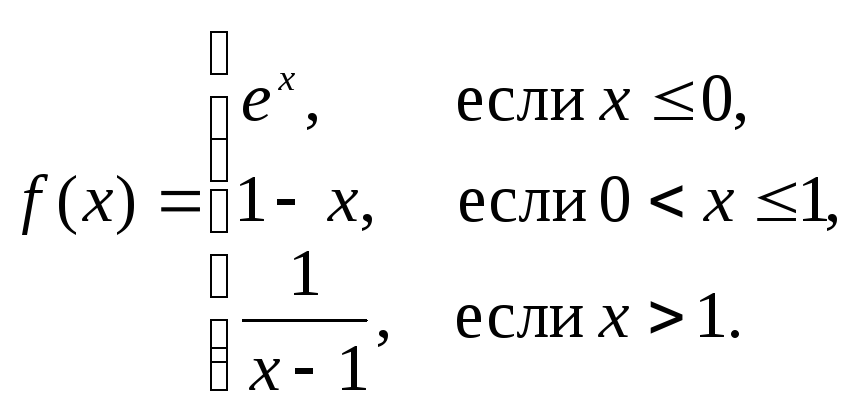
ж)
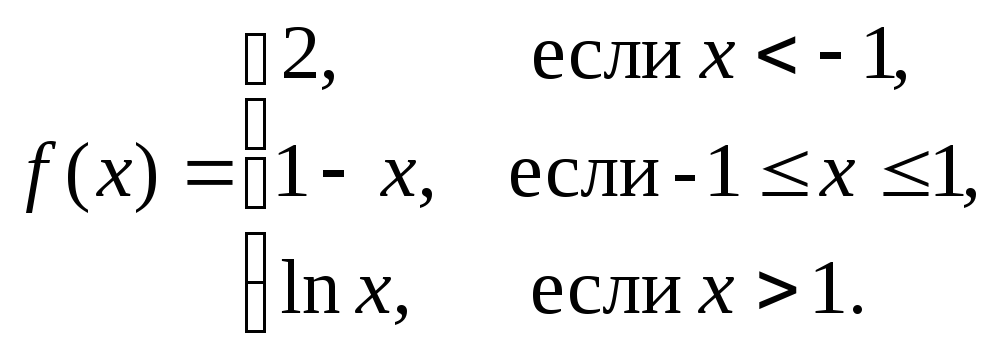 з)
з)