Задачи для самостоятельного решения
7. Функции нескольких переменных
1. Найти частные производные функций:
а)
; б)
; в)
;
г)
; д)
; е)
;
ж)
; з)
; и)
.
2. Найти полные дифференциалы функций:
а)
; б)
; в)
;
г)
; д)
; е)
.
3. а) Дана функция
.
Показать, что
.
б)
Дана функция
.
Показать, что
.
в)
Дана функция
.
Показать, что
.
4. Найти частные производные второго порядка для функций:
а)
; б)
;
в)
; г)
.
5. Найти экстремумы функций:
а)
; б)
;
в)
; г)
.
8. НеоПределенный иНтеграл
Определение 1.
Функция
называется первообразной для функции
на интервале
,
если она дифференцируема на
и для любого
выполняется равенство
.
Например, функция
является первообразной для функции
на всей числовой прямой, так как при
любом значении
,
т. е. выполняется равенство
;
функция
является первообразной для функции
на всей числовой прямой, так как в каждой
точке
.
Определение 2.
Множество всех первообразных функций
для функции
на интервале
называется неопределенным интегралом
от функции
на этом
интервале и обозначается символом
,
где
–
знак интеграла;
–
подынтегральная функция;
–
подынтегральное выражение;
–
переменная интегрирования.
Таким образом:
,
где
– некоторая первообразная для
на интервале
;
C
– произвольная
постоянная. Например, поскольку функция
является первообразной для функции
,
то
.
Операция нахождения неопределенного интеграла от данной функции называется интегрированием этой функции. Интегрирование представляет собой операцию, обратную дифференцированию.
Основные свойства неопределенного интеграла
Из определения неопределенного интеграла непосредственно вытекают следующие его свойства:
-
Производная от неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению:
.
-
Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
.
-
Постоянный множитель можно выносить за знак неопределенного интеграла:
(c
– const,
).
-
Неопределенный интеграл от алгебраической суммы непрерывных функций равен алгебраической сумме неопределенных интегралов:
.
-
Если
,
а
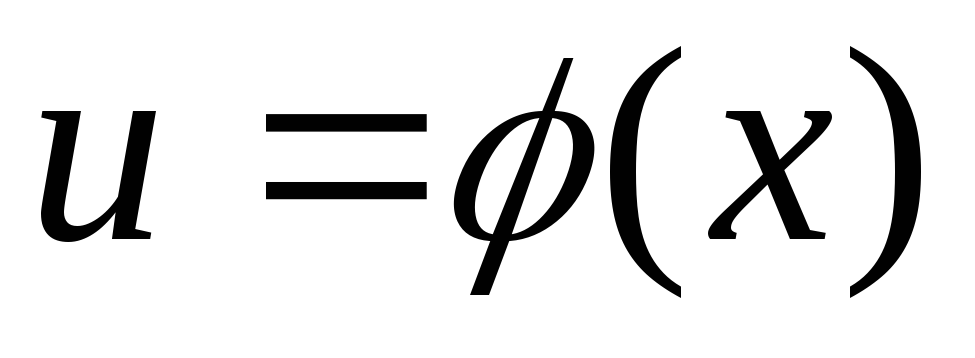– произвольная функция, имеющая
непрерывную производную, то
.
Таблица основных неопределенных интегралов
-
. -
. -
. -
. -
. -
. -
. -
. -
. -
. -
. -
. -
. -
. -
. -
.
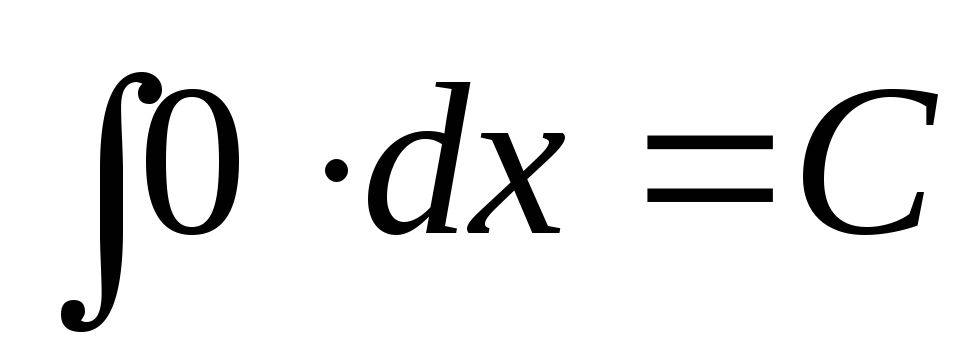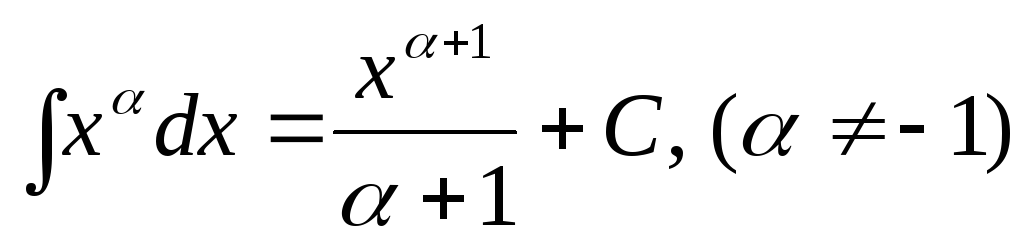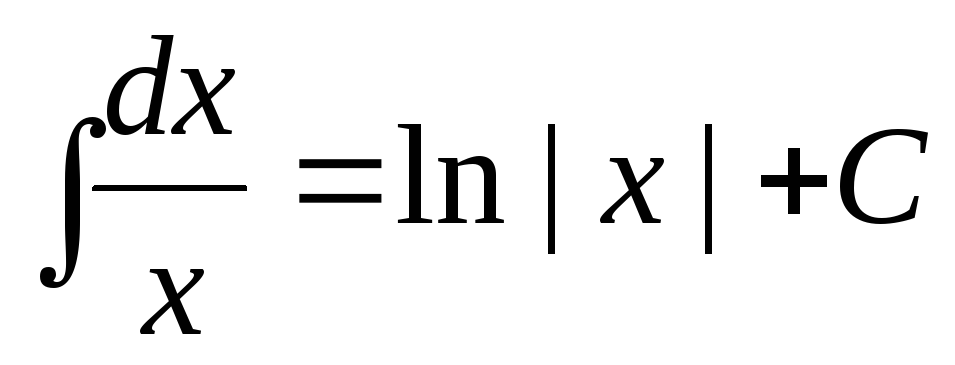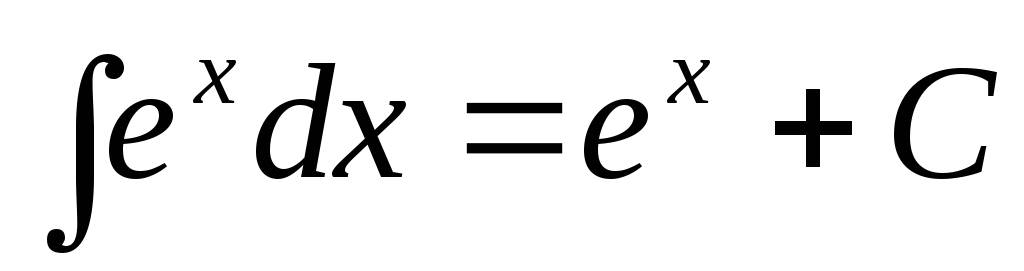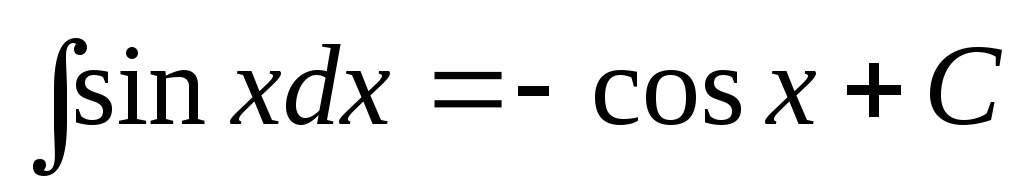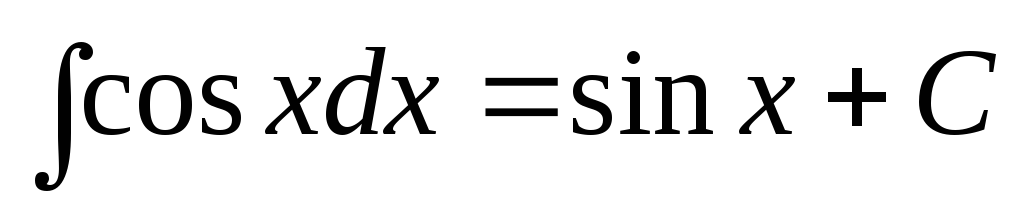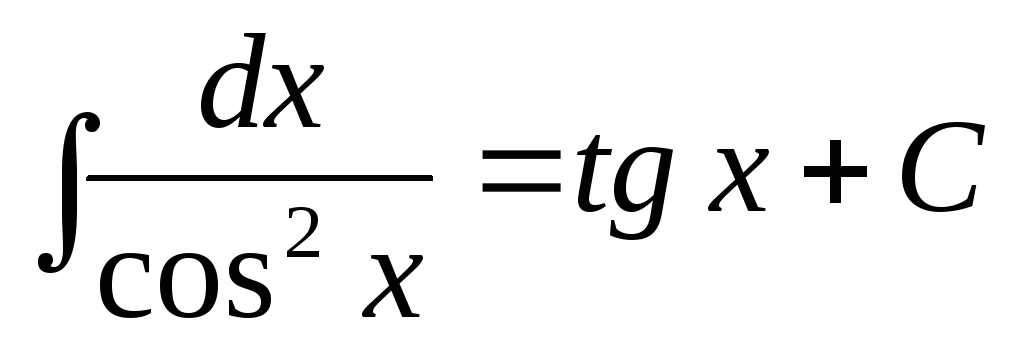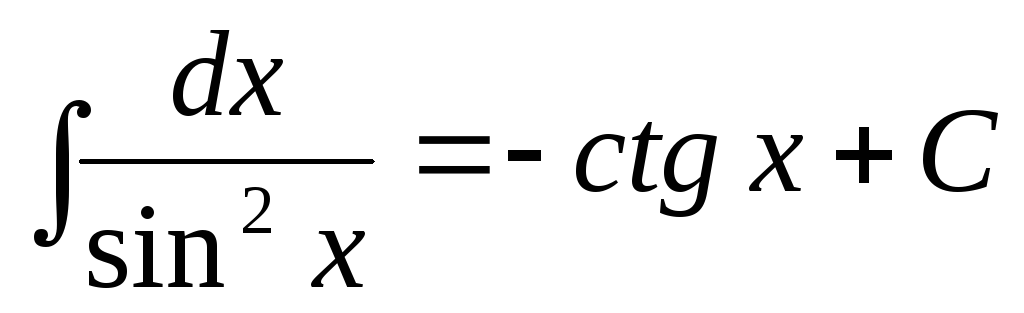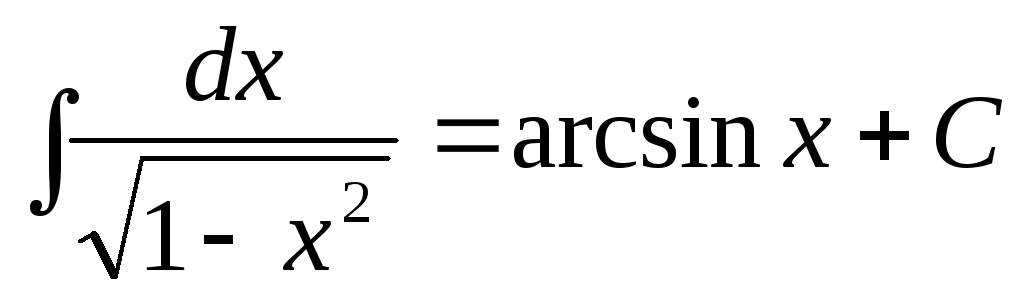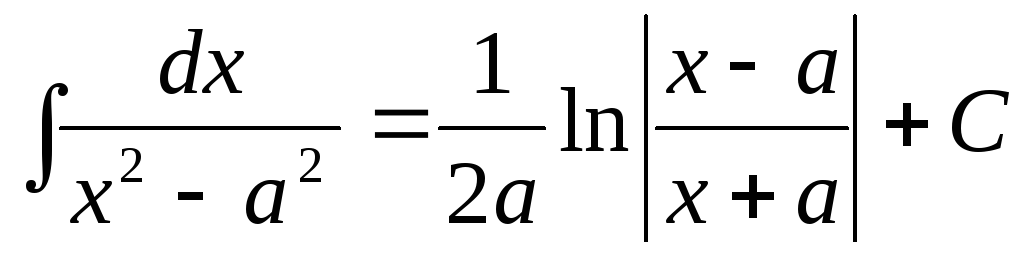Основные методы интегрирования а. Непосредственное интегрирование
При непосредственном вычислении неопределенных интегралов часто используются следующие преобразования дифференциала (операция «поднесения под знак дифференциала»):
,
,
,
,
.
В общем случае:
.
Пример 1.
Найти интеграл
.
Решение. Воспользуемся свойствами 3 и 4 неопределенного интеграла:
=
.
Пример 2.
Найти интеграл
.
Решение.
Для нахождения
данного интеграла воспользуемся
свойством 5
неопределенного интеграла. Так как
,
то
.