Точки разрыва функции и их классификация

Точки разрыва функции классифицируются следующим образом:

Определение 3. Точка называется точкой разрыва первого рода функции , если в этой точке существуют конечные пределы и , но они не равны между собой: . Величина называется скачком функции в точке .

Определение 4 . Точка называется точкой устранимого разрыва функции , если в этой точке существуют конечные пределы и , они равны между собой: , но сама функция не определена в точке или определена, но .

Определение 5. Точка называется точкой разрыва второго рода функции , если в этой точке хотя бы один из односторонних пределов ( или ) не существует или равен бесконечности.

Пример 3. Найти точки разрыва следующих функций и определить их тип:

а)

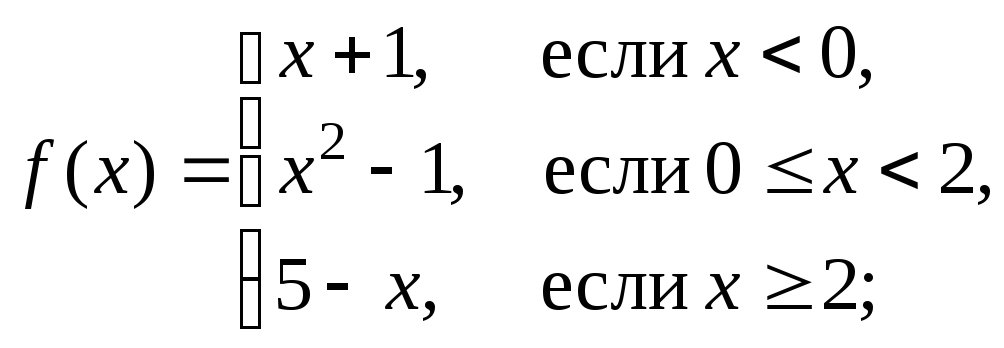
б)

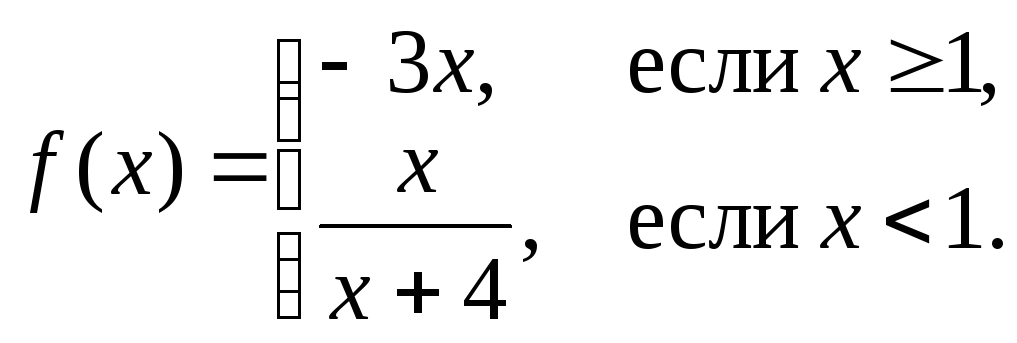
Решение:

а) функция определена и непрерывна на интервалах , и , так как на каждом из этих интервалов она задана непрерывными элементарными функциями. Следовательно, точками разрыва данной функции могут быть только те точки, в которых функция меняет свое аналитическое задание, т.е. точки и . Найдем односторонние пределы функции в точке :

, .

Так как односторонние пределы существуют и конечны, но не равны между собой, то точка является точкой разрыва первого рода. Скачок функции: .

Для точки находим:

,

, .

Таким образом, имеем: . Следовательно, в точке наша функция является непрерывной.

График данной функции изображен на рисунке:

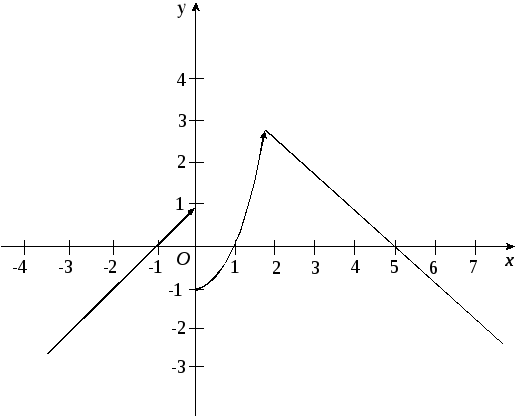
б) в точке функция меняет свое аналитическое задание, следовательно, в этой точке возможен разрыв. Найдем односторонние пределы:

,

, .

Так как , то точка является точкой разрыва первого рода. Скачок функции: .

В точке функция не определена, значит, точка является точкой разрыва. Определим ее тип:

, .

Следовательно, в точке функция имеет разрыв второго рода.

Задачи для самостоятельного решения

3. Непрерывность функции в точке

1. Исследовать следующие функции на непрерывность в указанных точках:

а) б) .

2. Доказать, что функция f(x) = ax² + bx + c непрерывна в любой точке х₀  R.

3. Найти точки разрыва следующих функций и определить их тип:

а) б)

4. Найти точки разрыва следующих функций:

а) ; б) .

4. Производная функции

Пусть функция f (х) определена в некоторой окрестности точки х₀.

Производной функции f (х) в точке х₀ называется число, обозначаемое f  (х₀) и равное

, (1)

если этот предел существует.

Так как х = х₀ + ∆х, х – х₀ = ∆х, то предел (1) может быть записан в виде:

, (2)

то есть производная функции f(x) в точке х₀ есть предел отношения ее приращения ∆f(х₀) в этой точке к соответствующему приращению аргумента ∆х, когда ∆х стремится к нулю.

Для обозначения производной функции f (x) в точке х₀ используют следующие выражения:

.

Правой производной называется число

. (3)

Аналогично определяется левая производная .

Заметим, что существование производной функции в точке равносильно равенству ее односторонних производных в этой точке.

Пример 1. Используя определение производной, найти для функции f (x) = 4x² – 1.

Решение

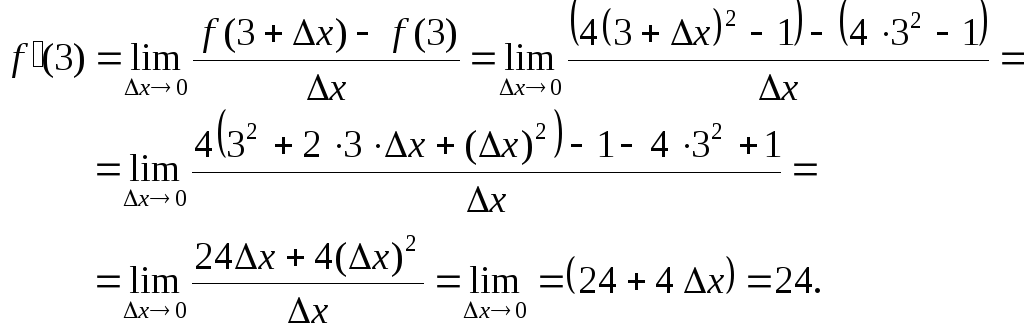
Ответ: = 24.

Пример 2. Найти односторонние производные функции f (x) = | x | в точке х₀ = 0.

Решение

Таким образом, функция f(x) = | x | в точке х₀ = 0 не имеет производной, так как односторонние производные не совпадают.

Ответ: = 1, .

(4)

– уравнение касательной к графику f (x) в точке х₀, причем,

,

где α – угол наклона касательной к положительному направлению оси 0х.

Следовательно, с геометрической точки зрения, производная функции f (x) в точке х₀ численно равна тангенсу угла, образованного касательной к графику функции f (x) в точке х₀ и положительным направлением оси 0х.

Прямая, перпендикулярная к касательной графика функции f (x) в точке , называется нормалью к кривой, определяемой функцией f (x), в точке х₀. Учитывая, что для перпендикулярных прямых k₁k₂ = –1, из (4) получаем уравнение нормали к графику функции f (x) в точке х₀:

. (5)

Операция вычисления производной функции называется дифференцированием. Функция, имеющая производную в точке, называется дифференцируемой в этой точке.