Е. Интегрирование тригонометрических функций
-
Интегралы вида
,
где R
– рациональная функция от
и
,
приводятся к интегралам от рациональных
функций с помощью подстановки
(универсальная тригонометрическая
подстановка).
Действительно,
,
,
,
,
тогда
,
где
– рациональная функция от переменной
.
Пример 8.
Вычислить интеграл
.
Решение.
Положим
,
тогда
,
,
.
Следовательно:
[переходя
к переменной x]
=
.
-
Интегралы вида
находятся с помощью
тригонометрических формул:
.
Пример 9.
Найти интеграл
.
Решение.
Так как
,
то
.
Задачи для самостоятельного решения
8. Неопределенный интеграл
1. Применяя метод непосредственного интегрирования, найти следующие интегралы:
a)
; б)
;
в)
; г)
.
2. Применяя метод замены переменной, найти следующие интегралы:
а)
; б)
;
в)
;
г)
;
д)
;
е)
.
3. Применяя метод интегрирования по частям, найти следующие интегралы:
а)
;
б)
;
в)
;
г)
;
д)
;
е)
.
4. Найти интегралы:
a)
;
б)
;
в)
;
г)
;
д)
;
е)
.
5. Найти интегралы:
а)
;
б)
;
в)
;
г)
;
д)
е)
9. ОПределенный иНтеграл
Пусть функция
определена на отрезке
,
.
Выполним следующие операции:
-
разобьем отрезок
точками
на n
частичных отрезков
; -
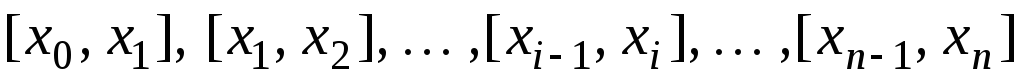в каждом из частичных отрезков
,
выберем произвольную точку
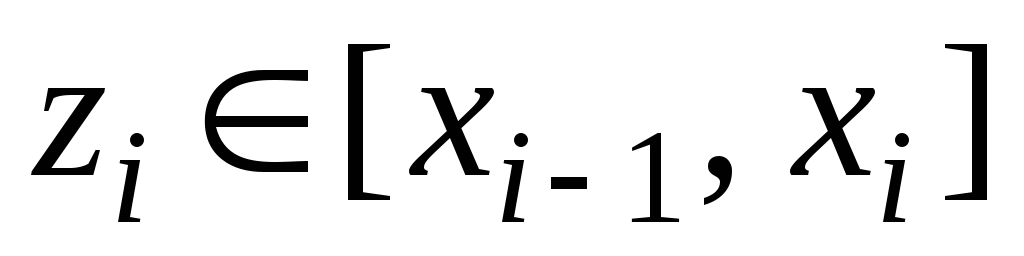и вычислим значение функции в этой
точке:
; -
найдем произведения
,
где
– длина частичного отрезка
,
; -
составим сумму
,
(1)
которая называется интегральной суммой функции y = f(x) на отрезке [а, b].