
- •1. Предел последовательности
- •Основные способы вычисления пределов
- •Задачи для самостоятельного решения
- •1. Предел последовательности
- •2. Предел функции Определение предела функции в точке по Коши
- •Предел функции в бесконечности
- •Точки разрыва функции и их классификация
- •Задачи для самостоятельного решения
- •3. Непрерывность функции в точке
- •4. Производная функции
- •Основные правила дифференцирования
- •Логарифмическое дифференцирование. Производная неявной функции. Производные высших порядков
- •Задачи для самостоятельного решения
- •4. Производная функции
- •5. Правило лопиталя. Дифференциал функции Раскрытие неопределенностей при помощи правила Лопиталя
- •Дифференциал функции
- •Задачи для самостоятельного решения
- •5. Правило Лопиталя. Дифференциал функции
- •6. Исследование функций
- •Общая схема построения графика функции
- •Задачи для самостоятельного решения
- •6. Исследование функций
- •7. Функции нескольких переменных
- •Задачи для самостоятельного решения
- •7. Функции нескольких переменных
- •8. НеоПределенный иНтеграл
- •Основные свойства неопределенного интеграла
- •Основные методы интегрирования а. Непосредственное интегрирование
- •Б. Метод замены переменной (подстановки)
- •В. Метод интегрирования по частям
- •Г. Интегрирование выражений, содержащих квадратный трехчлен
- •Д. Интегрирование простейших рациональных дробей
- •Е. Интегрирование тригонометрических функций
- •Задачи для самостоятельного решения
- •8. Неопределенный интеграл
- •9. ОПределенный иНтеграл
Частный институт управления и предпринимательства
Ю. В. Минченков
ВЫСШАЯ МАТЕМАТИКА
Сборник задач
по математическому анализу
Учебно-методическое пособие
Минск 2008
УДК 51
ББК 22.1я73
М 62
Рекомендовано к изданию редакционно-издательским советом Частного института управления и предпринимательства
А в т о р
заведующий кафедрой высшей математики и статистики Частного института управления и предпринимательства кандидат физико-математических наук, доцент Ю. В. Минченков
Р е ц е н з е н т ы:
доцент кафедры высшей математики и математической физики Белорусского государственного университета кандидат физико-математических наук, доцент А. А. Егоров;
доцент кафедры высшей математики и информатики Государственного института управления и социальных технологий БГУ кандидат физико-математических наук, доцент Н. Н. Рачковский
Рассмотрено и одобрено на заседании кафедры высшей математики и статистики, протокол № 2 от 19 сентября 2008 г.
Минченков, Ю. В.
М 62 Высшая математика. Сборник задач по математическому анализу: учеб.-метод. пособие / Ю. В. Минченков.– Минск: Частн. ин-т упр. и предпр., 2008.– 83 с.
ISBN 978-985-6877-23-3.
Приведены формулы, определения и другие краткие пояснения теории, необходимые для решения задач. Сборник содержит типовые задачи по математическому анализу с решениями и пояснениями.
Предназначен для самостоятельной работы студентов Частного института управления и предпринимательства.
УДК 51
ББК 22.1я73
© Минченков Ю. В., 2008
ISBN
978-985-6877-23-3 

 © Частный институт управления
и предпринимательства, 2008
© Частный институт управления
и предпринимательства, 2008
1. Предел последовательности
Бесконечной числовой последовательностью (или просто последовательностью) называется функция
![]() (1)
(1)
определенная на
множестве натуральных чисел. Каждое
значение
![]() называют элементом (или членом)
последовательности, а число п
– номером элемента последовательности.
Заметим, что последовательность всегда
содержит бесконечное число членов.
называют элементом (или членом)
последовательности, а число п
– номером элемента последовательности.
Заметим, что последовательность всегда
содержит бесконечное число членов.
Число а
называется пределом числовой
последовательности
![]() при
при
![]() ,
если для любого положительного сколько
угодно малого числа
,
если для любого положительного сколько
угодно малого числа
![]() существует номер
существует номер
![]() ,
такой, что для всех
,
такой, что для всех
![]() выполняется неравенство
выполняется неравенство
![]() . (2)
. (2)
Обозначается
![]() .
.
Математически данное определение можно записать в виде:
![]() .
.
Числовая
последовательность, имеющая конечный
предел, называется сходящейся.
Последовательность, не имеющая предела,
называется
рас-ходящейся. Если
![]() ,
то говорят, что последовательность
сходится к бесконечности.
,
то говорят, что последовательность
сходится к бесконечности.
Пример 1.
Доказать, что число
![]() является пределом последовательности
является пределом последовательности
![]() .
Найти, сколько элементов данной
последовательности не попало в
.
Найти, сколько элементов данной
последовательности не попало в
![]() -окрестность
числа
-окрестность
числа
![]() ,
если
,
если
![]() .
.
Решение. Из неравенства (2) следует
![]()
![]()
Таким образом,
![]() (целая часть числа, так как
(целая часть числа, так как
![]() – это номер элемента). Следовательно,
при
– это номер элемента). Следовательно,
при
![]()
![]() ,
т. е. число
,
т. е. число
![]() является пределом данной числовой
последовательности.
является пределом данной числовой
последовательности.
Пусть
![]() Следовательно, ровно 1999 элементов
находится за пределами интервала
Следовательно, ровно 1999 элементов
находится за пределами интервала
![]()
![]() .
.
![]() ,
,
![]() .
.
Числовая
последовательность
![]() называется бесконечно
большой последовательностью
(б.б.п.), если
называется бесконечно
большой последовательностью
(б.б.п.), если
![]() .
.
Числовая
последовательность
![]() называется бесконечно
малой последовательностью
(б.м.п.), если
называется бесконечно
малой последовательностью
(б.м.п.), если
![]() .
.
Основные способы вычисления пределов
При вычислении
пределов следует помнить, что
![]() .
.
Пример 2.
![]() = (делим числитель
и знаменатель на наивысшую степень п,
в данном случае на
= (делим числитель
и знаменатель на наивысшую степень п,
в данном случае на
![]() )
=
)
=
 .
.
Пример 3.
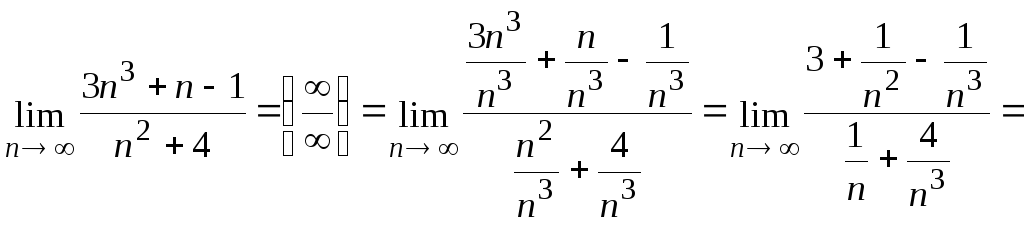
![]() .
.
Пример 4.

![]()
Пример 5
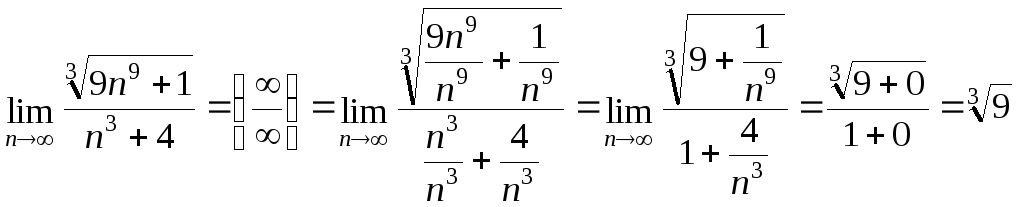 .
.
Пример 6
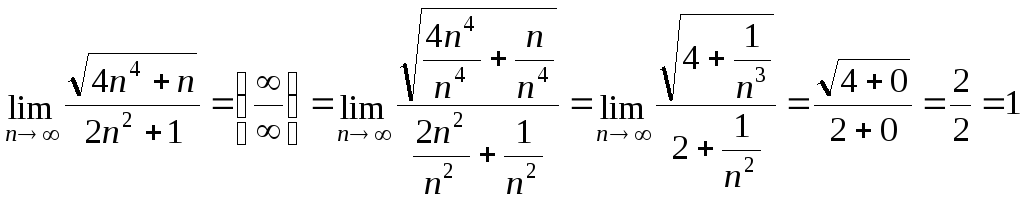 .
.
Анализируя примеры
2–6, можно сделать вывод, что когда мы
имеем неопределенность
![]() ,
предел равен:
,
предел равен:
-
отношению коэффициентов при старших степенях n, если степени n числителя и знаменателя равны;
-
0, если наивысшая степень n числителя меньше наивысшей степени n знаменателя;
-
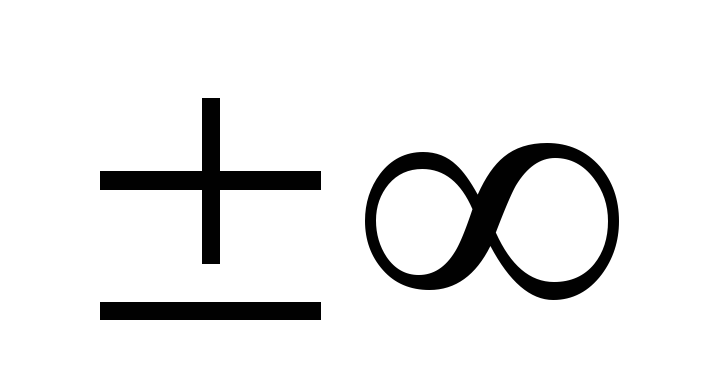 ,
если наивысшая степень n
числителя больше наивысшей степени n
знаменателя.
,
если наивысшая степень n
числителя больше наивысшей степени n
знаменателя.
Пример 7
![]()
![]()
![]() (делим
числитель и знаменатель на п)
(делим
числитель и знаменатель на п)
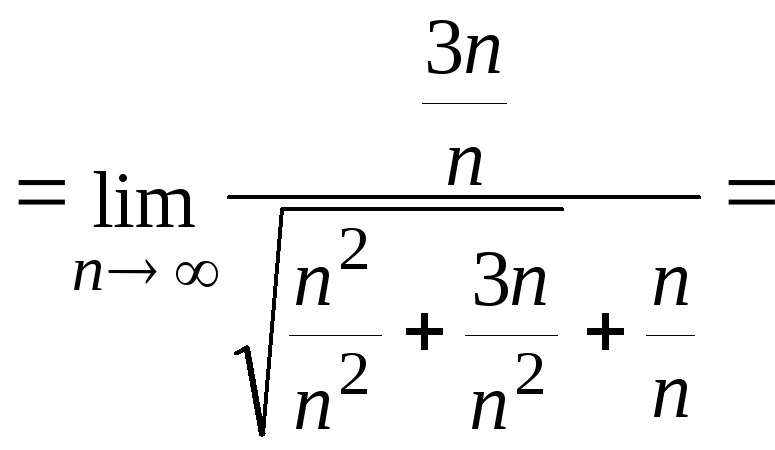
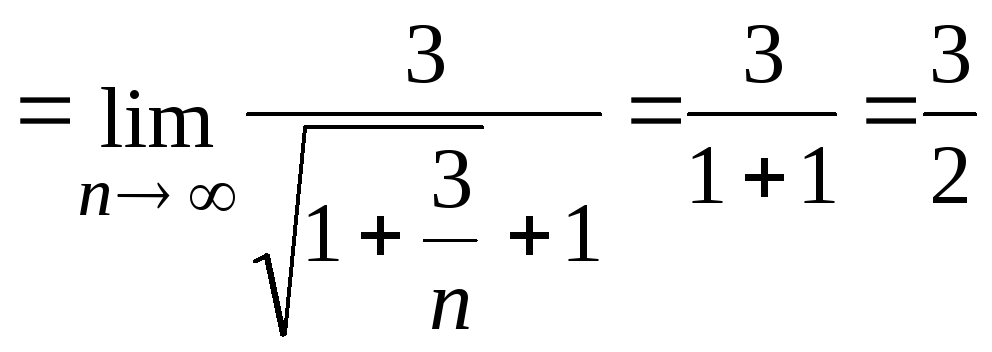 .
.
Вторым замечательным пределом будем называть предел:
![]() ,
(3)
,
(3)
где
![]() – иррациональное число.
– иррациональное число.
Заметим, что данный
предел представляет собой неопределенность
вида
![]() Он широко используется при вычислении
других пределов. Рассмотрим примеры.
Он широко используется при вычислении
других пределов. Рассмотрим примеры.
Пример
8.
![]() ,
так как
,
так как
![]() .
Заметим,
что если предел имеет вид, подобный виду
(3), то он равен е
(произведение второго слагаемого на
степень равно 1).
.
Заметим,
что если предел имеет вид, подобный виду
(3), то он равен е
(произведение второго слагаемого на
степень равно 1).
Пример 9
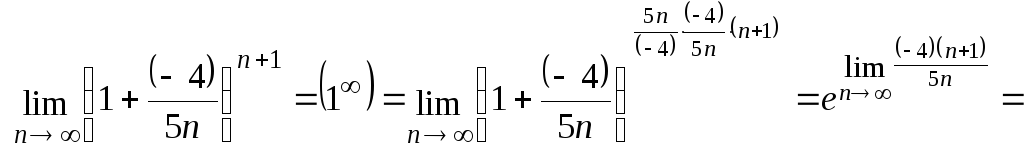
![]()
Пример 10
![]()
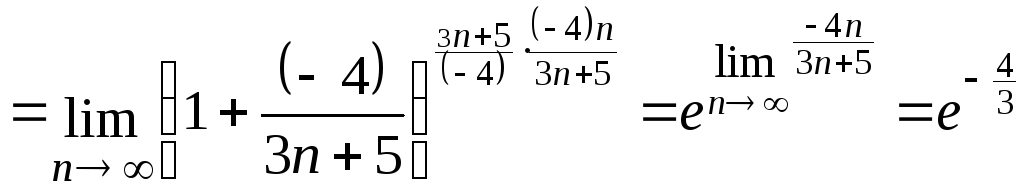 .
.
Задачи для самостоятельного решения
1. Предел последовательности
1.
Доказать, что число а
является
пределом последовательности
![]() .
Найти, сколько элементов данной
последовательности не попало в
.
Найти, сколько элементов данной
последовательности не попало в
![]() -окрест-ность
числа а:
-окрест-ность
числа а:
а)
![]() ;
;
б)
![]()
в)
![]()
г)
![]()
д)
![]()
2. Найти пределы:
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() ; д)
; д)
![]() е)
е)![]()
ж)
![]() з)
з)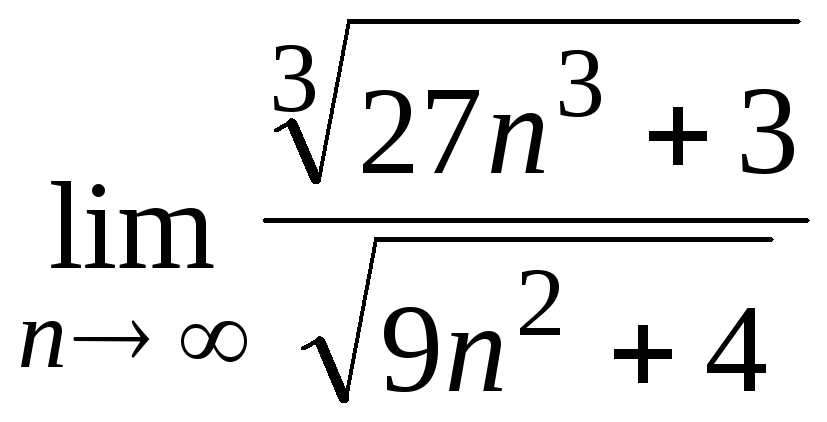 ; и)
; и)
![]()
к)
![]() ; л)
; л)
![]() ;
;
м)
![]() .
.
3. Найти пределы:
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() .
.
4. Найти пределы, используя второй замечательный предел:
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ;
;
г)
![]() ; д)
; д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)![]() ; к)
; к)![]() .
.
