
2) Пусть есть целая функция. Тогда ряд
![]() сходится
в пространстве
сходится
в пространстве
![]() .
.
Определение Для
целой функции
![]() отображение
отображение
![]() определяемое по правилу
определяемое по правилу
![]() ,
называется функцией от матрицы.
,
называется функцией от матрицы.
_____
Определение
Аннулирующий многочлен матрицы, который
имеет наименьшую степень и коэффициент
![]() при старшей степени,
при старшей степени,
называется минимальным.
ЗАМЕЧАНИЕ Если
![]() - показатель нильпотентности матрица
- показатель нильпотентности матрица
![]() ,
то минимальный аннулирующий многочлен
,
то минимальный аннулирующий многочлен
равен
![]() .
Его можно находить по формуле
.
Его можно находить по формуле
![]() ,
где
,
где
![]() есть наибольший общий делитель всех
есть наибольший общий делитель всех
алгебраических
дополнений матрицы
![]() .
.
Определение
Спектром матрицы
![]() называется последователь ность нулей
называется последователь ность нулей
![]() ее минимального аннулирующего много
ее минимального аннулирующего много
члена
![]() .
.
Определение Целые
функции
![]() совпадают на спектре
совпадают на спектре
![]() матрицы
матрицы
![]() ,
если
,
если
![]() .
.
ТЕОРЕМА 7.6 1)
(теорема Сильвестра) Если
![]()
то
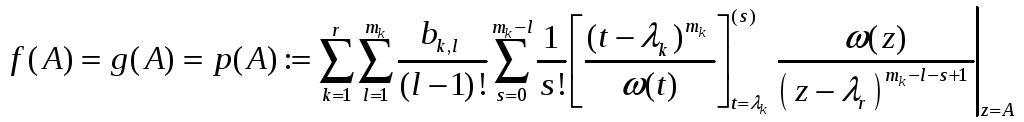 ,
,
где
![]() – интерполяционный многочлен Эрмита
с узлами
– интерполяционный многочлен Эрмита
с узлами
![]() и
и
значениями
![]() .
.
2) Если
![]() - ЖНФ матрица
- ЖНФ матрица
![]() и
и
![]() есть матрица перехода от
есть матрица перехода от
![]() к
к
![]() ,
то
,
то
![]() .
.
3) Для ЖНФ
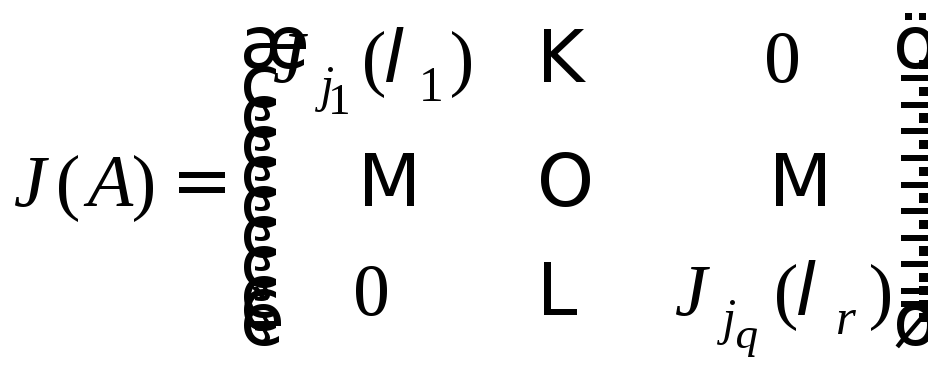 имеет место формула
имеет место формула
 .
.
4) Для жордановой
клетки
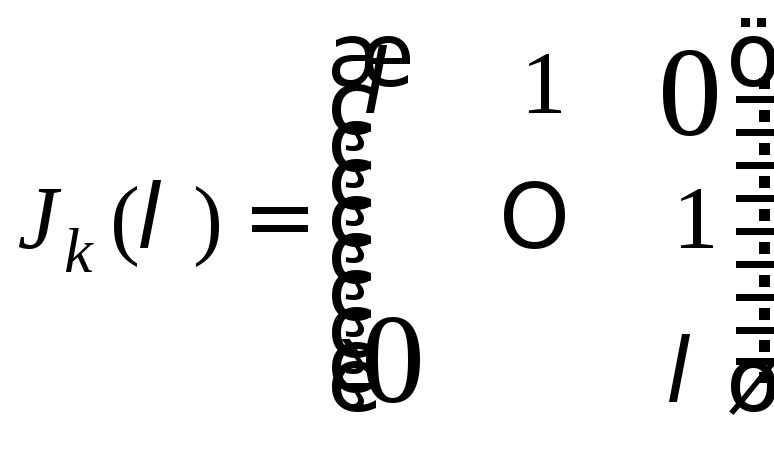 имеет место формула
имеет место формула
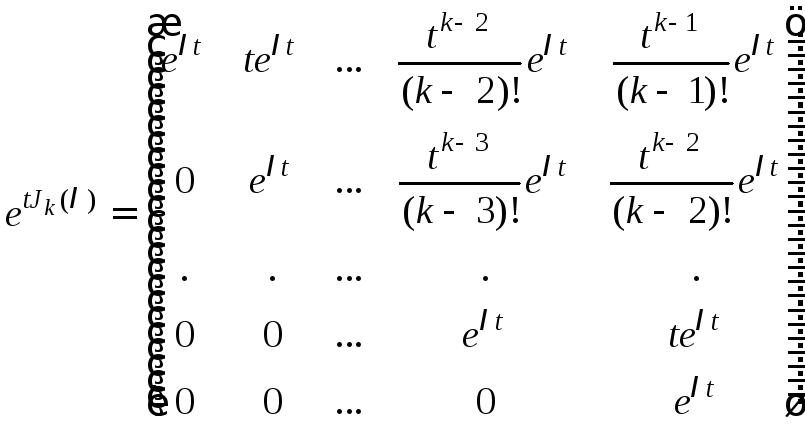 .
.
ЗАМЕЧАНИЕ
Пункты 2)-4) дают алгоритм построения
экспоненты от матрицы
![]() .
.
Понятие экспоненты от матрицы позволяет вывести формулу Коши для НСЛДУ с постоянными коэффициентами.
ТЕОРЕМА 7.7 (решение задачи Коши для НСЛДУ с постоян
ными коэффициентами)
Пусть в НСЛДУ
![]()
квадратная числовая
матрица
![]() имеет размер
имеет размер
![]() ,
а элементы
,
а элементы
матрицы
![]() непрерывны на
непрерывны на
![]() .
Тогда:
.
Тогда:
1) матрица
![]() является переходной матрицей НСЛДУ, то
является переходной матрицей НСЛДУ, то
есть фундаментальной
со свойством
![]() ;
;
2) общее решение
однородной НСЛДУ
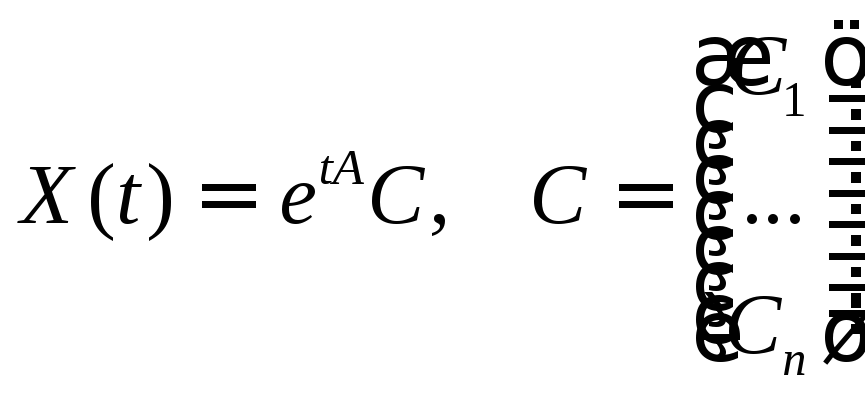 ;
;
3) решение задачи
Коши
![]() для однородной НСЛДУ имеет
для однородной НСЛДУ имеет
вид
![]() ;
;
4) решение задачи
Коши
![]() для неоднородной НСЛДУ имеет
для неоднородной НСЛДУ имеет
вид
![]() .
.
_____
Определение Сеткой
с шагом
![]() и узлами
и узлами
![]() называется раз
называется раз
биение отрезка
![]() точками
точками
![]() .
Сеточной функцией называется функция,
определенная в узлах
.
Сеточной функцией называется функция,
определенная в узлах
![]() .
.
Пусть правая часть
ОДУ
![]() имеет непрерывные в точке
имеет непрерывные в точке
![]() .
Тогда по формуле Тейлора в окрестности
точки
.
Тогда по формуле Тейлора в окрестности
точки
![]() для решения
для решения
![]() задача Коши:
задача Коши:
![]() ,
имеем
,
имеем
![]() .
.
Последнее равенство подводит к такому определению.
Определение Методом Эйлера приближенного решения задачи
Коши
![]() на сетке
на сетке
![]() называется нахождение
называется нахождение
сеточной функции
![]() по формулам
по формулам
![]() .
.
ЗАМЕЧАНИЕ Локальная погрешность метода Эйлера – это погреш
ность на одном
шаге, и она равна
![]() .
Глобальная погрешность – это
.
Глобальная погрешность – это
величина
![]() .
Для метода Эйлера она равна
.
Для метода Эйлера она равна
![]() .
.
Определение
Методом Рунге-Кутта приближенного
решения задачи Коши
![]() ,
на сетке
,
на сетке
![]() называется нахождение сеточной функции
называется нахождение сеточной функции
![]() по формулам
по формулам
![]() ,
где
,
где
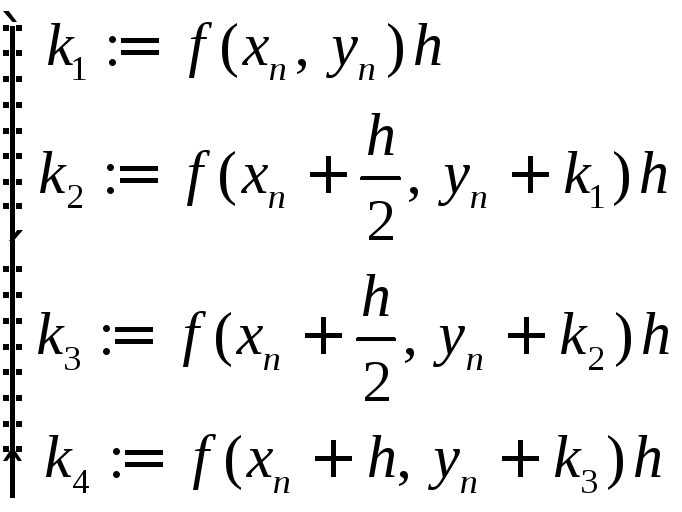 ,
,
![]() .
.
ЗАМЕЧАНИЕ 1 Локальная погрешность метода Рунге-Кутта на
одном шаге равна
![]() .
Глобальная погрешность равна
.
Глобальная погрешность равна
![]() .
.
ЗАМЕЧАНИЕ 2 Метод Рунге-Кута содержится, например, в
пакете Matlab.
_____
Определение НСОДУ
вида
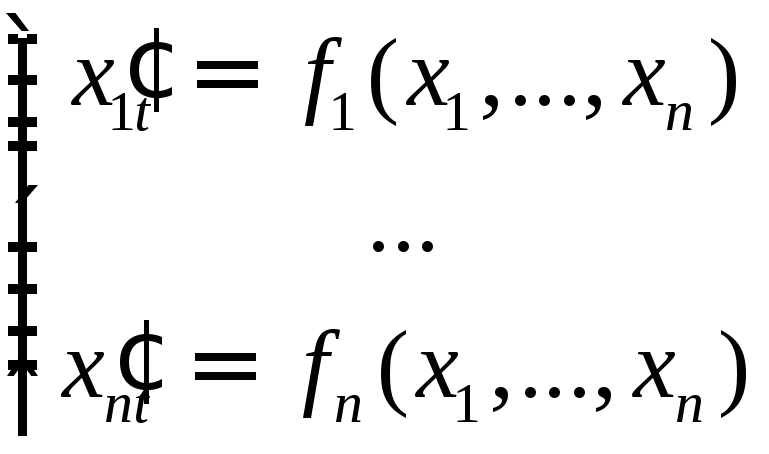 или в матричной
или в матричной
форме
![]() ,
где отображение
,
где отображение
![]() определено на откры том множестве
определено на откры том множестве
![]() ,
называется динамической (автономной)
системой (ДС).
,
называется динамической (автономной)
системой (ДС).
ЗАМЕЧАНИЕ
Предполагаем, что функции
![]() ,
,
удовлетворяют условию Липшица на любом замкнутом ограничен ном
множестве
![]() .
Тогда по теореме 7.1 задача Коши с
начальными
.
Тогда по теореме 7.1 задача Коши с
начальными
данными
![]() имеет единственное решение.
имеет единственное решение.
Определение
Множества точек
![]() в
в
![]() называются траекториями, а пространство
называются траекториями, а пространство
![]() -
фазовым пространством.
-
фазовым пространством.
ЗАМЕЧАНИЕ В силу теоремы единственности траектории
между собой не пересекаются. Траектории, определяемые
решениями
![]() ,
совпадают.
,
совпадают.
Определение
Постоянное решение
![]() динамической системы называется
положением равновесия.
динамической системы называется
положением равновесия.
ЗАМЕЧАНИЕ Из
определения следует, что точка
![]()
является положением равновесия динамической системы тогда и
только тогда, когда
она является решением системы
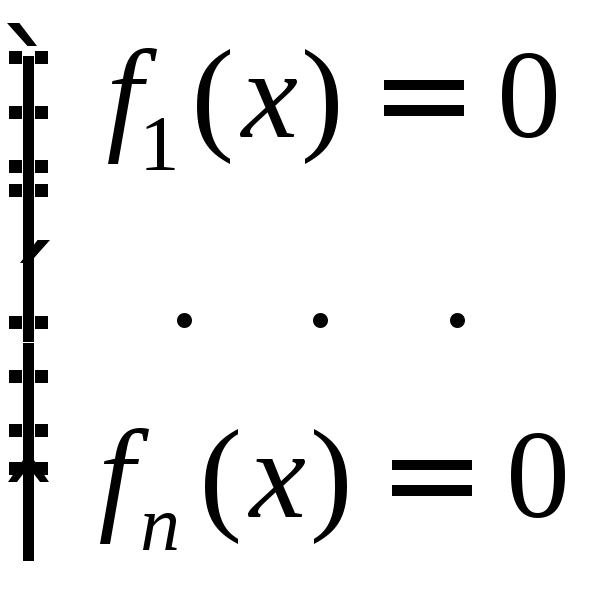 .
.
Определение
Решение динамической системы
![]() называется
называется
периодическим, а
соответствующая траектория в
![]() - замкнутой
- замкнутой
(циклом), если
![]() .
.
ЗАМЕЧАНИЕ Если траектория динамической системы сама
себя пересекает хотя бы в одной точке, то она необходимо
является либо положением равновесия, либо циклом (в силу
теоремы единственности).
Определение Множество траекторий динамической системы называется ее фазовым портретом.
Определение Цикл ДС называется предельным, если во множестве траекторий, проходящих через точки, достаточно близкие к этому циклу, нет замкнутых траекторий.
Определение Цикл
называется устойчивым (притягивающим),
если он
является асимптотой для всех траекторий,
проходящих через достаточно близкие к
этому циклу точки, при
![]() .
Цикл называется неустойчивым
(отталкивающим), если он является
асимптотой для всех близких траекторий
при
.
Цикл называется неустойчивым
(отталкивающим), если он является
асимптотой для всех близких траекторий
при
![]() .
.
Существуют альбомы фазовых портретов динамических систем.
_____
Напомним, что
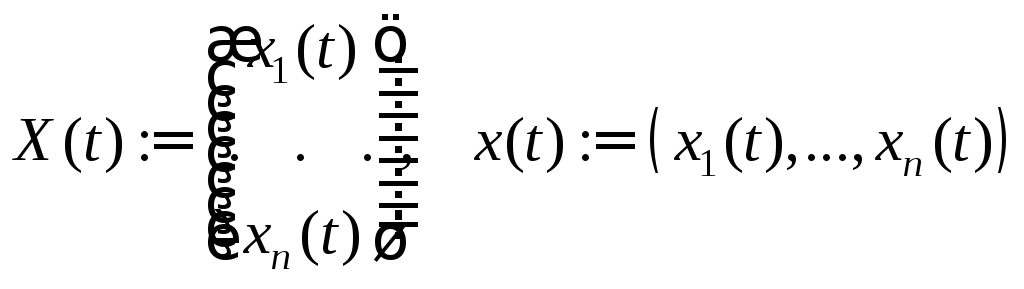 .
.
Определение Пусть
для НСОДУ
![]() выполнено условие теоремы единственности
на множестве точек
выполнено условие теоремы единственности
на множестве точек
![]() таких, что
таких, что
![]() .
Решение
.
Решение
![]() называется устойчивым по Ляпунову, если
называется устойчивым по Ляпунову, если
![]() с условием
с условием
![]() решение
решение
![]() задачи Коши с начальным условием
задачи Коши с начальным условием
![]() удовлетворяет условию:
удовлетворяет условию:
![]() .
Если кроме того
.
Если кроме того
![]() ,
то решение
,
то решение
![]() называется асимптотически устойчивым.
называется асимптотически устойчивым.
ЗАМЕЧАНИЕ
Устойчивость решения
![]() для НСОДУ
для НСОДУ
![]() равносильна
устойчивости нулевого решения для
равносильна
устойчивости нулевого решения для
НСОДУ
![]() .
.
СЛЕДСТВИЕ
Произвольное решение НСЛДУ![]()
устойчиво тогда и только тогда, когда устойчиво нулевой
решение однородного
уравнения
![]() .
.
Определение
Однородное ЛДУ с постоянными коэффициентами
![]() называется
устойчивым, если
называется
устойчивым, если
![]() решение
решение
![]() соответствующей задачи Коши
соответствующей задачи Коши
![]() ограничено на
ограничено на
![]() и
и
![]()
ТЕОРЕМА 7.8 (устойчивость ДУ)
1) Положение
равновесия
![]() однородной НСЛДУ с постоянными
однородной НСЛДУ с постоянными
коэффициентами
![]() устойчиво тогда и только тогда,
устойчиво тогда и только тогда,
когда собственные
числа матрицы
![]() имеют неположительные
имеют неположительные
вещественные части, а для чисто мнимых собственных чисел
![]() выполняется
равенство
выполняется
равенство
![]() .
.
2) В условиях
предыдущего пункта положение равновесия
![]()
асимптотически устойчиво тогда и только тогда, когда все
собственные
числа матрицы
![]() имеют отрицательные
имеют отрицательные
вещественные части.
3) (критерий Рауса-Гурвица) Однородное ЛДУ с постоянными
коэффициентами
![]() устойчиво тогда и
устойчиво тогда и
только тогда,
когда все главные миноры матрицы

положительны:
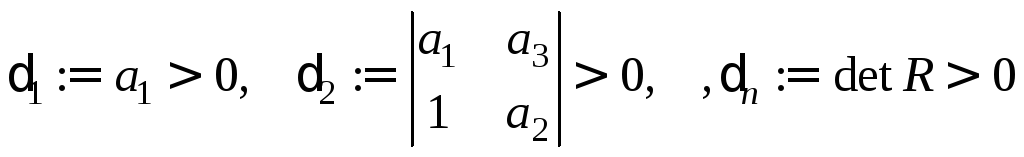 .
.
Определение Пусть
![]() - решение НСОДУ
- решение НСОДУ
 ,
которое назовем опорным (рабочим). Для
"близкого" решения
,
которое назовем опорным (рабочим). Для
"близкого" решения
![]() положим
положим
![]() .
Разложим функции
.
Разложим функции
![]() в окрестности
в окрестности
![]() по формуле Тейлора
по формуле Тейлора
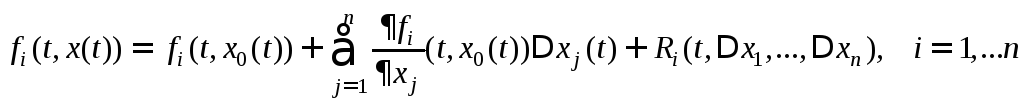 ,
,
или в матричной форме
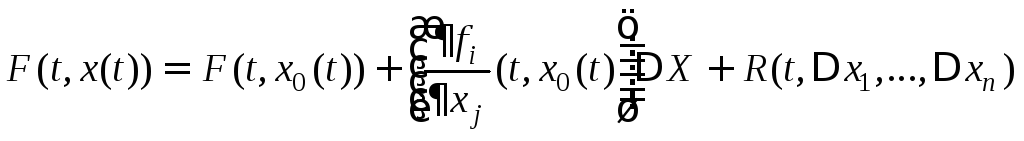 .
.
Тогда
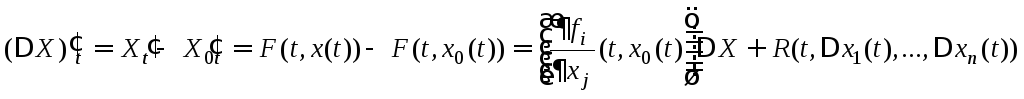 Отбрасывая последнее
слагаемое, получим НСЛДУ
Отбрасывая последнее
слагаемое, получим НСЛДУ
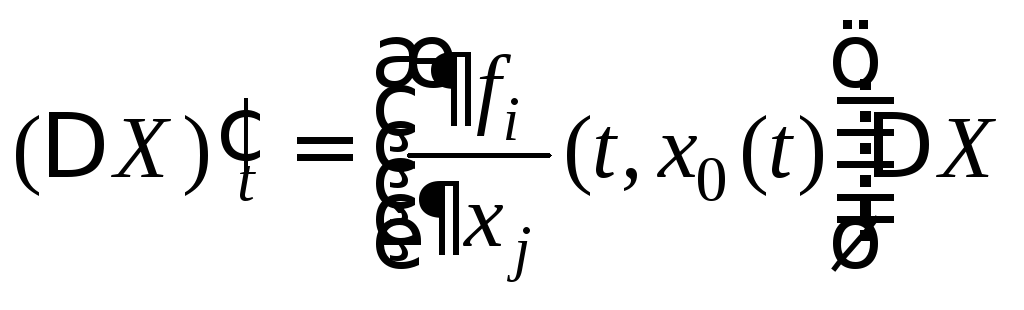 ,
,
которая называется
линеаризацией НСОДУ в окрестности
опорного решения![]() .
.
ЗАМЕЧАНИЕ Пусть
![]() - положение равновесия дина
- положение равновесия дина
мической системы
![]() ,
то есть
,
то есть
![]() ,
Тогда
,
Тогда
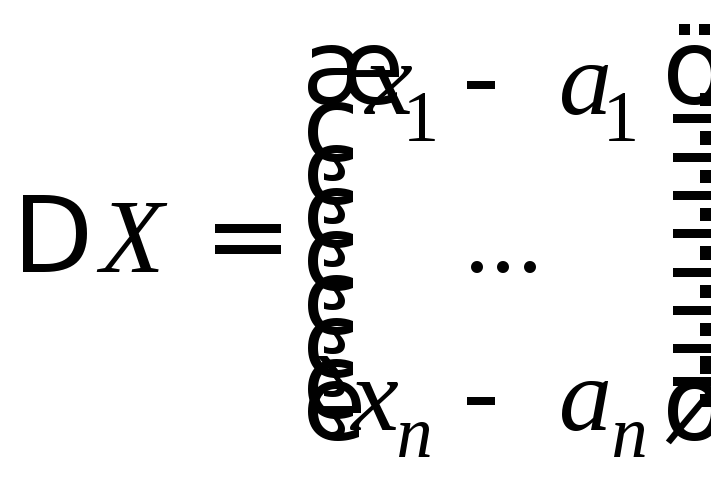
![]() ,
и потому линеаризацией динамической
системы в окре
,
и потому линеаризацией динамической
системы в окре
стности положения
равновесия
![]() будет НСЛДУ
будет НСЛДУ
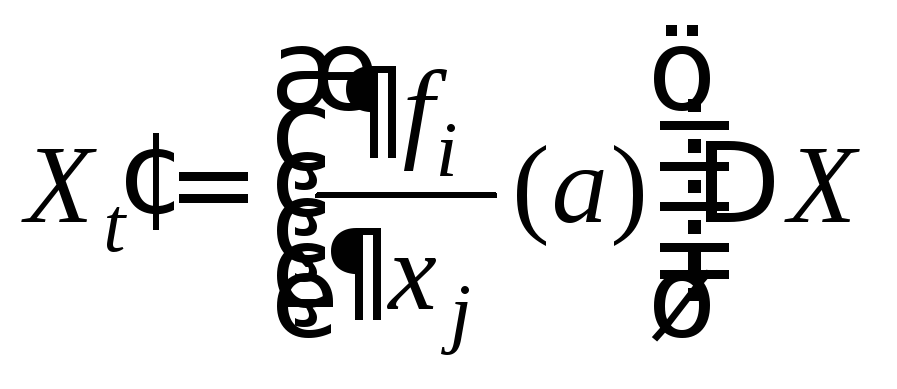
с постоянными коэффициентами. Решение последней находится по
формуле Коши.
ТЕОРЕМА 7.9
Пусть
![]() - положение равновесия
- положение равновесия
НСОДУ
![]() ,
то есть
,
то есть
![]() .
.
1) (теорема Ляпунова) Если линеаризация в окрестности этого поло
жения имеет
постоянную матрицу коэффициентов
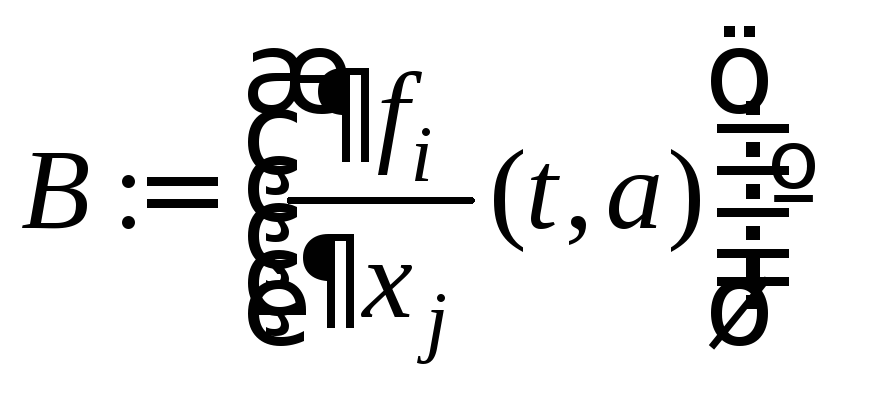
![]() и
и
![]() ,
где
,
где
![]() непрерывна в
непрерывна в
цилиндрической
области
![]() ,
то:
,
то:
а) если все
собственные числа матрицы
![]() имеют отрицательные
имеют отрицательные
вещественные
части, то положение равновесия
![]()
асимптотически устойчиво;
б) если хотя бы одно собственное число имеет положительную веще
ственную часть,
то положение равновесия
![]() неустойчиво.
неустойчиво.
2) (лемма Ляпунова)
Пусть НСОДУ
![]() удовлетворяет
удовлетворяет
условиям теоремы существования и единственности в "трубе"
![]() .
.
Пусть на шаре
![]() существует непрерывно
существует непрерывно
дифференцируемая
функция Ляпунова
![]() со свойством:
со свойством:
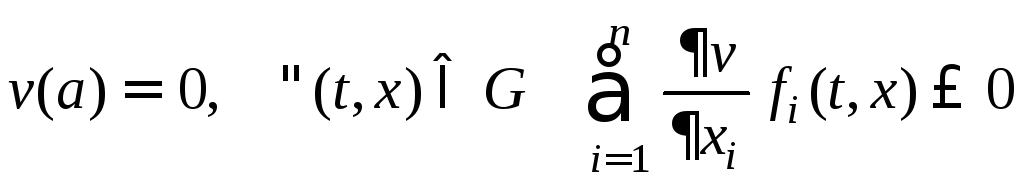 .
.
Тогда
![]() есть устойчивое положение равновесия.
есть устойчивое положение равновесия.
