
2) Решение исходного уравнения ищем в виде
![]() ,
считая в предыдущем решении произвольную
,
считая в предыдущем решении произвольную
постоянную зависящей
от
![]() (говорят: варьируя произвольную
(говорят: варьируя произвольную
постоянную
![]() ).
Для нахождения
).
Для нахождения
![]() подставим это решение в
подставим это решение в
исходное уравнение:![]() .
.
После сокращения получаем уравнение с разделяющимися
переменными для
нахождения
![]() .
.
____
ЗАМЕЧАНИЕ 1 Решение
ОДУ второго порядка вида
![]()
сводится к решению
ОДУ первого порядка
![]() с помощью
с помощью
замены
![]() .
.
ЗАМЕЧАНИЕ 2 Решение
ОДУ второго порядка вида
![]()
сводится к решению
ОДУ первого порядка с помощью замены
![]()
на зависимую
переменную
![]() .
.
_____
Определение Нормальной системой обыкновенных дифференциальных уравнений (НСОДУ) называется система вида
 ,
,
где функции
![]() непрерывны на открытом множестве
непрерывны на открытом множестве
![]() ,
а последовательность неизвестных
функций
,
а последовательность неизвестных
функций
![]() называется решением системы. Число
называется решением системы. Число
![]() называется порядком
НСОДУ.
называется порядком
НСОДУ.
Определение Если
![]() -
решение НСОДУ в окрестности точки
-
решение НСОДУ в окрестности точки
![]() ,
то кривая в
,
то кривая в
![]() называется интегральной
кривой.
называется интегральной
кривой.
Определение Пусть
![]() .
Задачей Коши для НСОДУ с начальными
условиями
.
Задачей Коши для НСОДУ с начальными
условиями
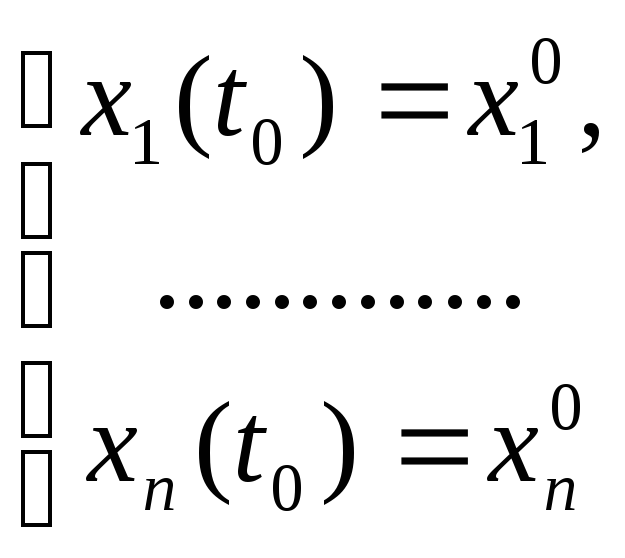 называется задача
нахождения решения системы в окрестности
точки
называется задача
нахождения решения системы в окрестности
точки
![]() ,
которое удовлетворяет этим условиям.
,
которое удовлетворяет этим условиям.
Пример Решение
задачи Коши для ОДУ
![]() го
порядка
го
порядка
![]() с начальными условиями
с начальными условиями
![]() равносильно нахождению решения задачи
Коши для НСОДУ
равносильно нахождению решения задачи
Коши для НСОДУ

с начальными
условиями
![]() .
.
Определение
Функция
![]() удовлетворяет условию Липшица по
переменным
удовлетворяет условию Липшица по
переменным
![]() на множестве
на множестве
![]() ,
если
,
если
![]()
![]()
ТЕОРЕМА 7.1 Пусть
функции
![]()
непрерывны на
открытом множестве
![]() и удовлетворяют
и удовлетворяют
условию Липшица
по
![]() на любом замкнутом ограниченном
на любом замкнутом ограниченном
подмножестве в
![]() .
Тогда
.
Тогда
![]() в окрестности точки
в окрестности точки
![]()
существует
единственное решение
![]() задачи Коши для
задачи Коши для
НСОДУ с начальным
условием
![]()
![]() .
Если
.
Если
отказаться от условия Липшица, то решение задачи Коши
существует, но оно, вообще говоря, неединственное.
Определение Нормальной системой линейных дифференциальных уравнений (НСЛДУ) называется система вида
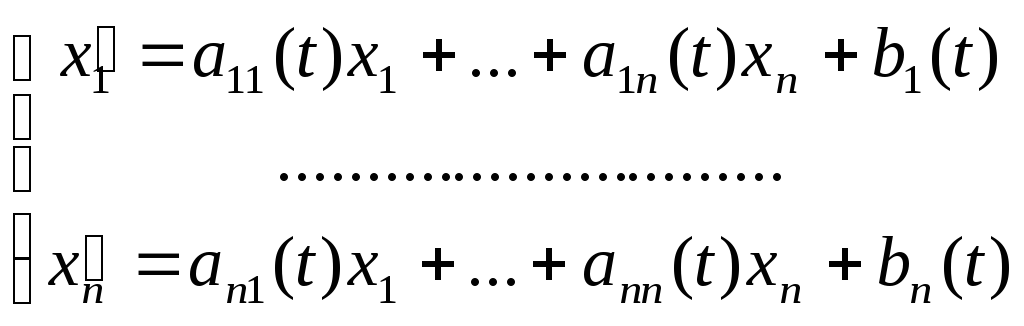
или в матричной
форме
![]() где
где
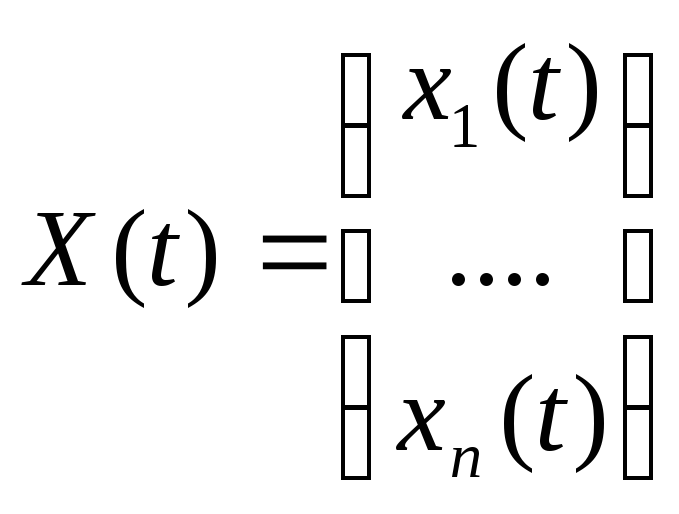 -
искомое решение на
-
искомое решение на
![]() ;
;
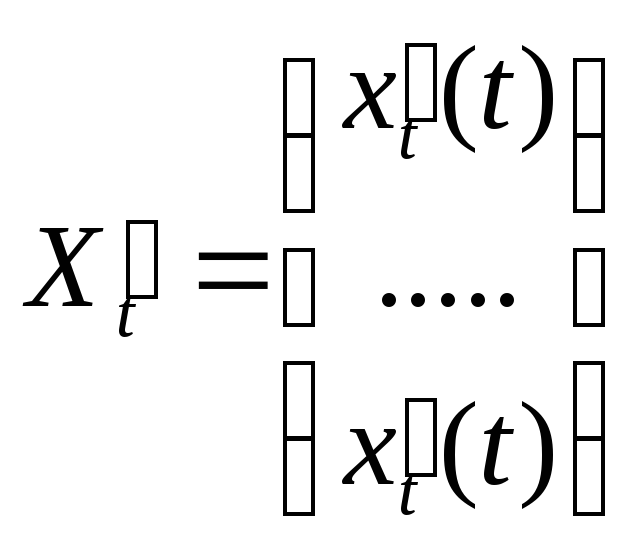 ;
;
 -
матрица непрерывных на
-
матрица непрерывных на
![]() коэффициентов;
коэффициентов;
 -
матрица непрерывных на
-
матрица непрерывных на
![]() свободных членов.
свободных членов.
Определение НСЛДУ
называется однородной,
если
![]()
![]() ,
и неоднородной в противном случае.
,
и неоднородной в противном случае.
Определение
Последовательность
![]() решений
решений
![]() однород ной НСЛДУ называется фундаментальной
системой, если
однород ной НСЛДУ называется фундаментальной
системой, если
![]() векторы
векторы
![]() линейно независимы. Определитель и
матрица
линейно независимы. Определитель и
матрица
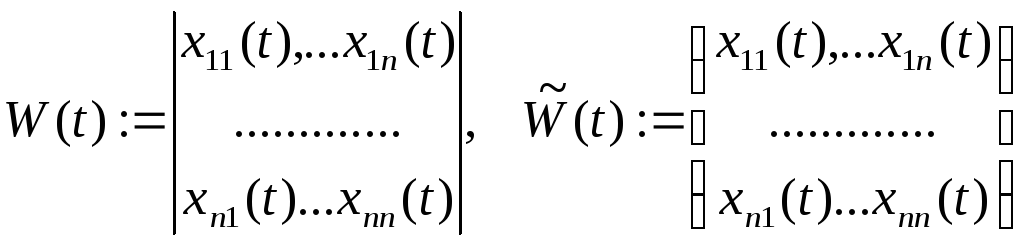
называются соответственно вронскианом и фундаментальной матрицей (матрицей Вронского) НСЛДУ.
Последняя есть пример функциональной матрицы.
Определение
Производной функциональной матрицы
![]()
называется
функциональная матрица
![]() ;
интегралом функциональной матрицы
;
интегралом функциональной матрицы
![]() на отрезке
на отрезке
![]() называется числовая матрица
называется числовая матрица
 .
.
ЗАМЕЧАНИЕ 1)
Постоянную матрицу-множитель
![]() можно
можно
выносить за знак
интеграла и производной:
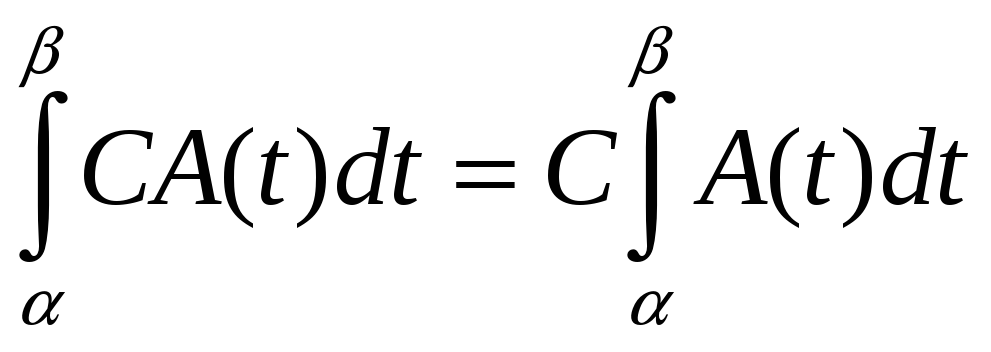 ,
,
![]() .
2)
.
2)
![]() .
.
Доказательство следует непосредственно из определения. Докажем, например, 2).
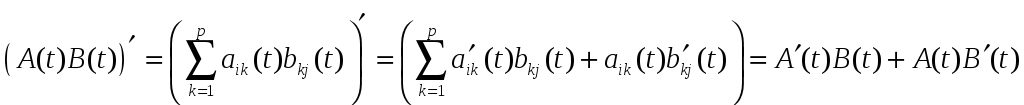 .
.
ТЕОРЕМА 7.2 (Свойства решений НСЛДУ)
1)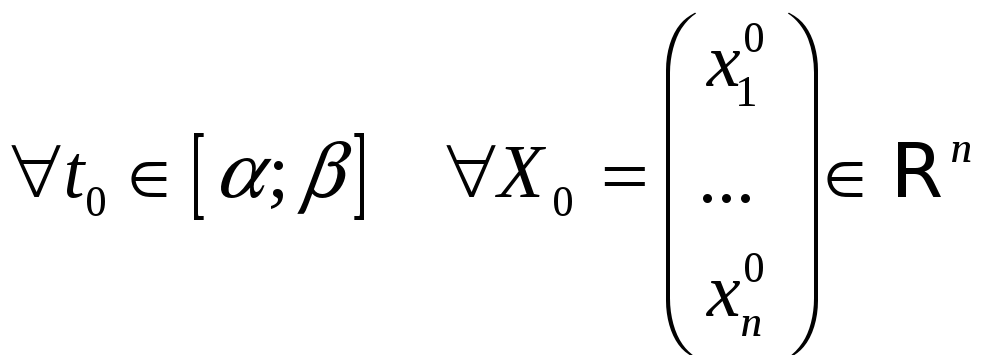 существует единственное решение на
существует единственное решение на
![]() задачи Коши с
начальным условием
задачи Коши с
начальным условием
![]() .
.
2) Систем
![]() решений
решений
![]() фундаментальна на отрезке
фундаментальна на отрезке
![]()
тогда и только
тогда, когда
![]() ;
;
3) Если система
решений
![]() фундаментальна на
фундаментальна на
![]() ,
то
,
то
общее решение
однородной НСЛДУ
![]() имеет вид
имеет вид
![]() .
.
4) Если
![]() -
какое-либо (частное) решение неоднородной
НСЛДУ,
-
какое-либо (частное) решение неоднородной
НСЛДУ,
то общее (любое) решение этой НСЛДУ имеет вид
![]() ,
,
где
![]() -
фундаментальная система.
-
фундаментальная система.
5) если известна
фундаментальная система
![]() ,
то частное
,
то частное
решение неоднородной НСЛДУ можно вычислить по формуле
 ,
а решение задачи Коши с начальным
,
а решение задачи Коши с начальным
условием
![]() - по формуле Коши
- по формуле Коши
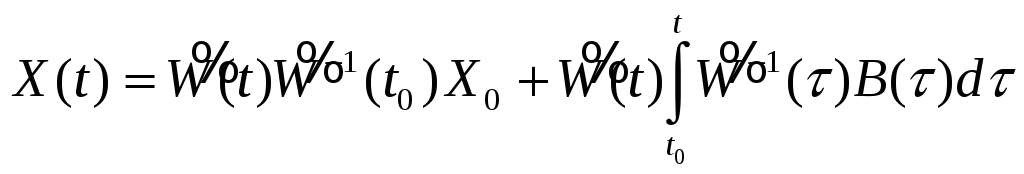 ,
где
,
где
 .
.
Определение Если
![]() - фундаментальная матрица НСЛДУ, то
матрица
- фундаментальная матрица НСЛДУ, то
матрица
![]() называется переходной (импульсной)
матрицей этой системы.
называется переходной (импульсной)
матрицей этой системы.
ЗАМЕЧАНИЕ 1) Переходная матрица является решением задачи
Коши для матричного
уравнения
![]() с функциональной
с функциональной
матрицей
![]() размера
размера
![]() и начальным условием
и начальным условием
![]() ,
,
где
![]() есть единичная матрица.
есть единичная матрица.
2) Переходная матрица не зависит от выбора фундаментальной системы и
полностью
определяется матрицей коэффициентов
![]() НСЛДУ.
НСЛДУ.
3) В терминах переходной матрицы формула Коши принимает вид
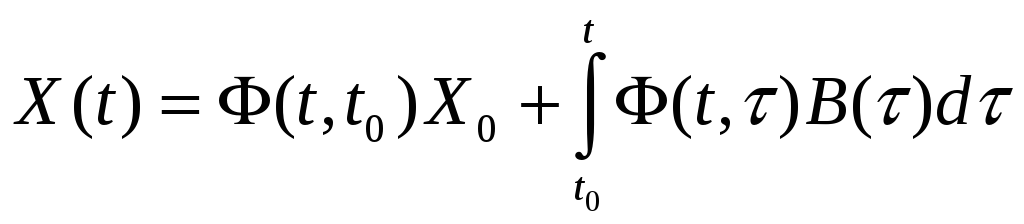 .
.
_____
Определение
Линейным
дифференциальным уравнением
![]() -го
порядка (ЛДУ) называется
ОДУ вида
-го
порядка (ЛДУ) называется
ОДУ вида
![]() ,
(1)
,
(1)
где функции
![]() непрерывны на
непрерывны на
![]() .
ЛДУ называется однородным, если
.
ЛДУ называется однородным, если
![]() и неоднородным в противном случае.
и неоднородным в противном случае.
Определение
Последовательность решений
![]() однородно ЛДУ
однородно ЛДУ
![]() -го
порядка называется
линейно независимой
на
-го
порядка называется
линейно независимой
на
![]() ,
если в каждой точке
,
если в каждой точке
![]() векторы
векторы
![]()
![]() линейно независимы.
линейно независимы.
Определение
Последовательность
![]() линейно независимых на
линейно независимых на
![]() решений однородного уравнения называется
фундаментальной.
решений однородного уравнения называется
фундаментальной.
Определение Определителем Вронского и фундаментальной матрицей однородного ЛДУ называются соответственно
 ,
,
где
![]() есть последовательности линейно
независимых решений.
есть последовательности линейно
независимых решений.
ТЕОРЕМА 7.3 (свойства
решений ЛДУ
![]() -го
порядка)
-го
порядка)
1)
![]() задача Коши с начальным условием
задача Коши с начальным условием
![]() имеет единственное
решение на
имеет единственное
решение на
![]() .
.
2) Решения
![]() однородного ЛДУ линейно независимы на
однородного ЛДУ линейно независимы на
![]() тогда и только
тогда, когда
тогда и только
тогда, когда
![]() .
.
3) Если
![]() -
фундаментальная последовательность
-
фундаментальная последовательность
решений однородного ЛДУ, то любое (общее) его решение имеет
вид
![]()
4) Если
![]() -какое-либо
решение ЛДУ (1) и
-какое-либо
решение ЛДУ (1) и
![]() - фундамен
- фундамен
тальная последовательность решений, то любое (общее) решение
ЛДУ можно записать
в виде
![]() .
.
5) Если известна
фундаментальная последовательность
![]() ,
,
то решение задачи Коши для уравнения (1) можно искать по
формуле Коши для этого уравнения
 ,
,
где
![]() есть
алгебраическое дополнение соответствующего
есть
алгебраическое дополнение соответствующего
элемента
фундаментальной матрицы
![]() .
.
Определение
Матрицы
![]() называются подобными,
если существует невырожденная матрица
называются подобными,
если существует невырожденная матрица
![]() (матрица перехода от
(матрица перехода от
![]() к
к![]() )
со свойством
)
со свойством
![]() .
.
Определение Если к множеству собственных векторов,
соответствующих
собственному числу
![]() добавить нулевой вектор,
добавить нулевой вектор,
то получим
подпространство
![]() пространства в
пространства в
![]() .
Его
.
Его
называют подпространством собственных векторов.
Цель параграфа - обосновать подобные рассуждения в общем случае.
Определение Если
![]() - собственный вектор, соответствующий
собственному числу
- собственный вектор, соответствующий
собственному числу
![]() ,
то
,
то
![]() ым
присоединенным вектором матрицы к
ым
присоединенным вектором матрицы к
![]() называется вектор
называется вектор
![]() со свойством
со свойством
![]() .
.
Определение Вектор
![]() имеет высоту
имеет высоту
![]() ,
если
,
если
![]() .
.
ЗАМЕЧАНИЕ Вектор
![]() высоты
высоты
![]() является
является
![]() -ым
-ым
присоединенным
вектором к собственному вектору
![]() .
.
Обратно,
![]() -ый
присоединенный вектор
-ый
присоединенный вектор
![]() имеет высоту
имеет высоту
![]() .
.
Определение
Последовательность
![]() собственного и присоединенных к нему
векторов называется жордановой цепочкой
длины
собственного и присоединенных к нему
векторов называется жордановой цепочкой
длины
![]() матрицы
матрицы
![]() .
То есть длина жордановой цепочки
совпадает с высотой ее последнего
присоединенного вектора.
.
То есть длина жордановой цепочки
совпадает с высотой ее последнего
присоединенного вектора.
ЗАМЕЧАНИЕ Пусть собственные векторы, образующие
жордановы цепочки
![]() ,
линейно независимы
,
линейно независимы
и порождены одним
и тем же собственным числом
![]() .
Тогда все
.
Тогда все
векторы, составляющие эти цепочки, линейно независимы.
В силу сделанного
замечания жорданова цепочка имеет длину
![]() .
Из импликации
.
Из импликации
![]() следует такая цепь вложений
следует такая цепь вложений
![]() .
.
Так как каждый
ненулевой вектор из
![]() является собственным или присоединенным
(высотой
является собственным или присоединенным
(высотой
![]() ),
то есть входит в какую-то цепочку, то
эти пространства, начиная с некоторого
),
то есть входит в какую-то цепочку, то
эти пространства, начиная с некоторого
![]() ,
обязаны совпадать.
,
обязаны совпадать.
Определение
Наименьшее число
![]() ,
начиная с которого все подпространства
,
начиная с которого все подпространства
![]() совпадают, называется показателем
нильпотентности матрицы
совпадают, называется показателем
нильпотентности матрицы
![]() ,
а подпространство
,
а подпространство
![]() - корневым подпространством матрицы
- корневым подпространством матрицы
![]() .
.
ЗАМЕЧАНИЕ Корневое подпространство является инвариант
ным относительно матричного оператора:
![]() ,
,
и образовано из нуля и всех собственных и присоединенных
векторов,
соответствующих собственному числу
![]() .
.
_____
Определение
Система цепочек
называется жордановым базисом корневого
подпространства
![]() .
.
ЗАМЕЧАНИЕ По
построению
![]() есть число жордановых
есть число жордановых
цепочек длины
![]() .
Оно вычисляется по формуле
.
Оно вычисляется по формуле
![]() .
( 1 )
.
( 1 )
Общее число цепочек, составляющих базис равно
![]() .
.
_____
Определение
Суммой подпространств
![]() векторного пространства
векторного пространства
![]() называется множество
называется множество
![]() .
.
Из определения следует такое
ЗАМЕЧАНИЕ
![]() - подпространство.
- подпространство.
Определение Сумма
ненулевых подпространств
![]() называется прямой, если
называется прямой, если
![]() .
.
Обозначение
![]() .
.
Определение
Квадратную матрицу
![]() ,
элементами
,
элементами
которой являются
многочлены
![]() ,
можно представить в виде матричного
многочлена
,
можно представить в виде матричного
многочлена
![]() ,
где
,
где
![]() -
матрица-коэффициент при
-
матрица-коэффициент при
![]() .
Если
.
Если
![]() ,
то
,
то
![]() называется матричным многочленом n-ой
степени.
называется матричным многочленом n-ой
степени.
Определение
Многочлен
![]() называется
аннулирующим многочленом матрицы
называется
аннулирующим многочленом матрицы
![]() ,
если многочлен от матрицы
,
если многочлен от матрицы
![]() равен нулевой матрице:
равен нулевой матрице:
![]() .
.
ЗАМЕЧАНИЕ (теорема Гамильтона-Кели) Характеристический
многочлен
![]() матрицы
матрицы
![]() является ее аннулирующим
является ее аннулирующим
многочленом.
СЛЕДСТВИЕ Если
![]() - показатель нильпотентности матрицы
- показатель нильпотентности матрицы
![]() ,
где
,
где
![]() есть нуль порядка
есть нуль порядка
![]() характеристического
характеристического
многочлена матрицы
![]() ,
то
,
то
![]() .
.
ТЕОРЕМА 7.4 Пусть
![]() есть
есть
характеристический
многочлен матрицы
![]() ,
,
![]() - показатель ниль
- показатель ниль
потентности
матрицы
![]() и
и
![]() - жорданов базис корневого
- жорданов базис корневого
подпространства
![]() .
Тогда
.
Тогда
![]() (=
(=![]() )
)
и
![]() есть базис в
есть базис в
![]() (в
(в
![]() ),
если все собственные
),
если все собственные
числа вещественные (не все вещественные).
Определение
Построенный в теореме базис
![]() называется жордановым базисом матрицы
называется жордановым базисом матрицы
![]() .
.
Определение Матрица
![]() есть матрица оператора умножения на
есть матрица оператора умножения на
![]() в естественном базисе пространства
в естественном базисе пространства
![]() (
(![]() ).
Найдем матрицу этого оператора в
жордановом базисе. Столбцы искомой
матрицы по определению составлены из
коэффициентов разложения элементов
вида
).
Найдем матрицу этого оператора в
жордановом базисе. Столбцы искомой
матрицы по определению составлены из
коэффициентов разложения элементов
вида
![]() или вида
или вида
![]() в жордановом базисе. Поэтому искомая
матрица образована матрицами вида
в жордановом базисе. Поэтому искомая
матрица образована матрицами вида
 ,
( 2 )
,
( 2 )
размер которых
совпадает с длиной цепочки, в которую
входит
![]() .
Эти матрицы «нанизаны» на главную
диагональ, а элементы вне этих
.
Эти матрицы «нанизаны» на главную
диагональ, а элементы вне этих
матриц равны нулю.
Так построенная квазидиагональная
матрица называется жордановой нармальной
формой (ЖНФ) матрицы
![]() и обозначается
и обозначается
![]() .
Матрицы вида (2) называются
.
Матрицы вида (2) называются
![]() -жордановыми
клетками соответствующего порядка.
-жордановыми
клетками соответствующего порядка.
ТЕОРЕМА 7.5 (свойства подобных матриц)
1) Матрицы
![]() и
и
![]() подобны, причем матрица
подобны, причем матрица
![]() ,
,
столбцами которой
являются элементы жорданова базиса
![]() ,
,
является матрицей
перехода от
![]() к
к
![]() .
.
2) ЖНФ матрицы
![]() не зависит от выбора жорданова базиса
и
не зависит от выбора жорданова базиса
и
единственная с точностью до перестановки клеток.
3) Характеристические многочлены подобных матриц совпадают.
![]() .
.
4) Если матрицы
![]() ,
и
,
и
![]() - жорданов базис
- жорданов базис
матрицы
![]() ,
то
,
то
![]() будет
жордановым базисом матрицы
будет
жордановым базисом матрицы
![]() .
.
5) Две квадратные матрицы одинакового размера подобны тогда и
только тогда, когда их жордановы нормальные формы совпадают.
АЛГОРИТМ (построения матрицы перехода и ЖНФ)
1) Находим собственные числа как корни характеристического
уравнения
![]() .
.
2) Для каждого
собственного числа
![]() описываем неубывающую
описываем неубывающую
последовательность
подпространств
![]() и
и
вычисляем ранги матриц, останавливаясь, как только ранги
стабилизируются. В результате получаем показатель нильпотент
ности
![]() и количества жордановых клеток одинакового
размера
и количества жордановых клеток одинакового
размера
![]() .
.
3) Для каждого
собственного числа
![]() Находим в параметрической
Находим в параметрической
форме расширяющуюся последовательность подпространств
решений однородных
СЛАУ
![]() .
В
.
В
каждом из подпространств выделяем множество линейно
независимых присоединенных векторов, не принадлежащих
предыдущему подпространству. по ним образуем цепочки. Из
полученных цепочек
составляем базисы
![]() корневых
корневых
подпространств,
а из этих последних – жорданов базис
![]() .
.
4) Из координат
элементов базиса
![]() как из столбцов составляем
как из столбцов составляем
матрицу перехода
![]() ,
а по показателям нильпотентности
,
а по показателям нильпотентности
![]() и
и
соответствующим
числам
![]() - ЖНФ
- ЖНФ
![]() .
.
В связи со сделанным замечанием дадим такое
Определение
Переход от жордановой нормальной формы
![]() с комплексными элементами и матрицей
перехода
с комплексными элементами и матрицей
перехода
![]() к вещественным матрицам
к вещественным матрицам
![]() и
и
![]() называется операцией
овеществления жордановой нормальной
формы.
называется операцией
овеществления жордановой нормальной
формы.
ЗАМЕЧАНИЕ (решение НСЛДУ с постоянными коэффициента
ми методом
расщепления) Пусть требуется найти
общее решение НСЛДУ
![]() .
Подставляя
.
Подставляя
![]() в систему и делая замену
в систему и делая замену
![]() ,
получаем новую НСЛДУ
,
получаем новую НСЛДУ
![]() .
Эта система распадается на более простые
независимые НСЛДУ в количестве, равном
числу клеток Жордана матрицы
.
Эта система распадается на более простые
независимые НСЛДУ в количестве, равном
числу клеток Жордана матрицы
![]() .
Число таких подсистем, вообще говоря,
уменьшится, если мы овеществим ЖНФ.
.
Число таких подсистем, вообще говоря,
уменьшится, если мы овеществим ЖНФ.
______
Интерполяционные многочлены понадобятся для получения формулы Коши решения НСЛДУ с постоянными коэффициентами. Сплайны же естественно излагать вместе с интерполяционными многочленами.
Определение Задачей простой интерполяции на последователь
ности попарно
различных узлов
![]() называется задача нахождения многочлена
называется задача нахождения многочлена
![]() ,
принимающего в этих узлах наперед
заданные значения
,
принимающего в этих узлах наперед
заданные значения
![]() .
.
ЗАМЕЧАНИЕ Многочленом наименьшей степени, решающим
задачу простой интерполяции, является интерполяционный
многочлен в форме Лагранжа
![]() ,
,
где
![]() .
.
Определение Задачей
кратной интерполяции на последовательности
попарно различных узлов
![]() с кратностями соответственно
с кратностями соответственно
![]() называется задача нахождения многочлена
называется задача нахождения многочлена
![]() ,
принимающего в этих узлах
,
принимающего в этих узлах
![]() вместе со своими производными до порядка
вместе со своими производными до порядка
![]() включительно наперед заданные значения
включительно наперед заданные значения
![]() .
.
ЗАМЕЧАНИЕ
Многочленом наименьшей степени
![]() ,
,
решающим задачу кратной интерполяции, является интерполяционный
многочлен в форме Эрмита
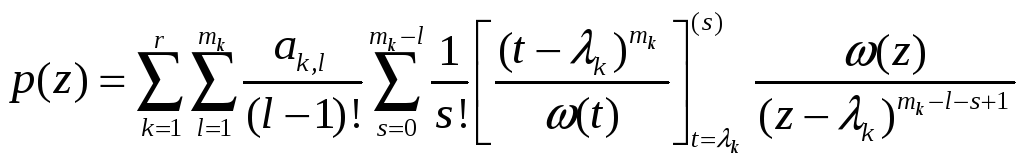 ,
,
где
![]() .
.
_____
Определение Сеткой
с узлами
![]() на
отрезке
на
отрезке
![]() называется
называется
разбиение
![]() .
.
Определение
Сплайном степени
![]() на сетке
на сетке
![]() называется функция
называется функция
![]() ,
имеющая на
,
имеющая на
![]() непрерывные производные до
непрерывные производные до
![]() -го
порядка включительно, которая совпадает
на каждом отрезке
-го
порядка включительно, которая совпадает
на каждом отрезке
![]() с каким-либо многочленом степени
с каким-либо многочленом степени
![]() и хотя бы на одном отрезке – с многочленом
степени
и хотя бы на одном отрезке – с многочленом
степени
![]() .
.
Пример 1
![]() - линейный сплайн. Его график есть
ломаная.
- линейный сплайн. Его график есть
ломаная.
Пример 2
![]() - кубический сплайн. Он является дважды
непрерывно дифференцируемой на
- кубический сплайн. Он является дважды
непрерывно дифференцируемой на
![]() функцией, а его график составлен из
кубических парабол.
функцией, а его график составлен из
кубических парабол.
АЛГОРИТМ (построения кубического сплайна)
1) Заданы узлы,
соответствующие значения в узлах
![]() и два
и два
дополнительных
значения
![]() первой или второй производной на
первой или второй производной на
каком-либо из
концов.
![]() .
.
2) Обозначим
![]() .
Тогда из определения кубического сплайна
.
Тогда из определения кубического сплайна
следует
![]() .
.
Неизвестные
![]() находим из условий
находим из условий
![]() :
:
![]() .
.
Подставляя их в
![]() ,
получаем рабочую формулу
,
получаем рабочую формулу

![]()
3) Из условий
![]() ,
получаем основную СЛАУ
,
получаем основную СЛАУ
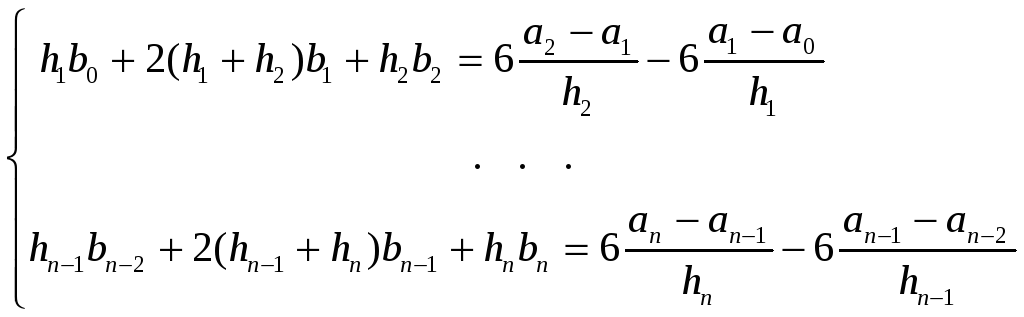
c
![]() уравнениями и
уравнениями и
![]() неизвестными
неизвестными
![]() .
Добавляем к ним
.
Добавляем к ним
два уравнения со
значениями
![]() .
.
4) Решаем полученную СЛАУ, и решение подставляем в рабочую
формулу
![]() .
.
Определение
Кубический сплайн называется естественным,
если два дополнительных условия имеют
вид
![]() ,
и периодическим, если они имеют вид
,
и периодическим, если они имеют вид
![]() и
и
![]() .
.
_____
Ниже нам понадобятся некоторые определения и результаты из функционального анализа.
Определение
Последовательность элементов
![]() нормированного пространства
нормированного пространства
![]() называется сходящейся к элементу
называется сходящейся к элементу
![]() ,
если
,
если
![]() .
Последовательность элементов
.
Последовательность элементов
![]() назы вается фундаментальной, если
назы вается фундаментальной, если
![]() .
.
ЗАМЕЧАНИЕ Каждая сходящаяся последовательность фундаментальна. Обратное, вообще говоря, неверно.
Определение Нормированное пространство, в котором каждая фундаментальная последовательность сходится, называется полным (банаховым).
ЗАМЕЧАНИЕ 1)
Пространство матриц
![]() со скалярным
со скалярным
произведением
![]() является
полным.
является
полным.
