3. Колебательная система

Стационарные состояния x₁=0,x₂=0.

Для решения системы выполним преобразование:

.

Решение:

Г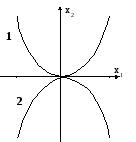рафик решений:

Данное уравнение описывает гиперболическую зависимость. В данной системе строго периодические процессы невозможны. Точка О  точка бифуркации (раздвоения). Для перехода на другую ветвь гиперболы не требуется затрат энергии. Этот переход возможен при сколь угодно слабом внешнем влиянии. Это один из примеров, когда полностью детерминированное уравнение, без случайных членов, описывает случайные процессы.

Один из основателей operation research (исследования операций) Акофф утверждает, что важнейшими проблемами науки  века будет выяснение того, как:

1. из детерминированного порядка может получиться хаос (см. предыдущий пример);

2. из хаоса получится порядок и развитие системы. Этот вопрос рассматривается в теории самоорганизации  синергетике).

4. Колебательная нелинейная система.

x₂=0, f(x₁)=0  точки равновесия.

В системе возможны периодические процессы, есть бифуркация. Могут проявляться две особенности:

 существование предельных циклов;

 существование странных аттракторов.

Внутри предельного цикла может быть область (странный аттрактор), каждая точка которой является точкой бифуркации, т.е. поведение системы абсолютно непредсказуемо. Система может попасть внутрь этой области, минуя предельный цикл, извне благодаря случайному импульсу. Время выхода из аттрактора и его направление предсказать невозможно.

Примеры странных аттракторов:

1. область максимальных ошибок управления самолётом (если самолёт идёт на малой скорости, с большим углом атаки, то попадает в область максимальных ошибок управления  реакция машины непредсказуема. В этом случае пилоты руководствуются правилом: не знаешь что делать  не делай ничего);

2. экономика в состоянии кризиса, извне её вывести из кризиса нельзя. Единственный способ выхода из кризиса - перестройка внутренней структуры системы;

3. пограничные состояния психики.

Критерий Бендиксона.

Он показывает, когда решения системы общего вида , где P и Q  нелинейные функции, не содержат аттракторов. Для этого необходимо, чтобы выражение в заданом диапазоне параметров значений x₁ и x₂ было знакопостоянным.

Один из примеров такого уравнения  экологическое уравнение Вольтерра

Эти уравнения определяют изменение численности видов в системе “хищник-жертва”. Пусть у нас будут только две популяции: рыси и зайцы. Интерпретация:

x₁  cреднемесячная численность зайцев;

x₂  cреднемесячная численность рысей;

a  вероятность размножения зайцев;

b  естественная смертность зайцев;

c  вероятность того, что при встрече зайца с рысью заяц будет съеден;

e  естественная смертность рысей;

d  скорость размножения зайцев, которая зависит от количества зайцев.

Решение уравнения Вольтерра имеет вид:

Эти решения проявляют определённую периодичность с некоторым относительным смещением по фазе кривых

5. Уравнение Лоренца имеет вид:

Оно описывает возникновение стохастических автоколебаний.

Примеры таких процессов: погодные явления  тайфуны, циклоны; океанические течения; нерегулярные колебания дерева под влиянием постоянной силы ветра.

Для решений уравнения характерна непредсказуемость фазовых траекторий, которые заполняют двумерную бесконечную поверхность, пересечение которых с некоторой прямой образует канторово множество точек.

Решения уравнения Лоренца содержат странные аттракторы или стохастические ловушки и образует счётные множества неустойчивых циклов. Внешние флюктуации не могут вывести систему из этого состояния.

6. Системы с запаздыванием.

а) x(t)=ax(t-), где   запаздывание.

Это колебательная система, точка равновесия x=0.

Уравнение даёт квазипериодическое решение вида e^at(a₀cost+b₀sint), где a₀, b₀  медленноизменяющиеся функции времени.

в) x(t)=f(t-), f  нелинейная функция. Частный случай: x(t)=x(a-bx(t-)). Если >>1/a, то система идёт вразнос, колебания расходящиеся. Если =0, то она стремится к равновесию.

Возможны периодические процессы при однозначной функции f(t). Нелинейная система уравнений с запаздыванием

Начальные условия:x₁(t)=₁(t), -<t0, x₂(t)=₂(t), -<t0.

Данные уравнения описывают стохастическую случайную систему.

Запаздывание равносильно увеличению степеней свободы и сложности систем (экологическая система).

Линейные системы с запаздыванием могут быть эргодическими. Стабильные системы с запаздыванием должны иметь обратные связи. Если такая система молодая, то внутрисистемные процессы в ней не развиты и компенсация в них невелика. При очень большом числе системных процессов снижается эффективность.

Нелинейная система с =0 и переменными коэффициентами.

Если коэффициенты a_i меняются, то проходят когда-нибудь через такие значения, которые соответствуют появлению странных аттракторов на фазовой плоскости решений. Начальные условия в таких уравнениях действуют только до первой стохастической области. Дальше они просто теряют своё значение.

Данная система является статистически предсказуемой. Причём программное развитие её определяют коэффициенты a_ki(t), а память  задержка . Чем больше , тем более предсказуема система. Если уравнение переходит в , то появляются предельные циклы и странные аттракторы. Если нет явной зависимости от x(t), значит в системе не принимаются оперативные решения. Если запаздывание в этих уравнениях только в нелинейных членах, то возникают лакуны (полости) на фазовой плоскости решений. Лакуна  это область, которая не соответствует никакому решению. Вероятнее всего, наличие лакуны показывает неадекватность уравнения. Однако в некоторых случаях оно имеет физический смысл. Когда параметры системы такие, что она приближается к лакуне, это значит, что система на грани распада. Данные уравнения могут описывать развитие как самопроизвольное усложнение и упорядочивание структур.

Распределённые системы.

В таких системах, в отличие от рассмотренных ранее дискретных систем, нельзя чётко выделить элементы и связи.

1.  уравнение теплопроводности и диффузии.

Если в уравнении есть производные по времени только чётных порядков, то оно описывает обратимые во времени процессы, иначе присутствуют необрати-мые процессы. Обратимые процессы  это процессы, возвращение которых в начальное состояние не требует дополнительных затрат энергии.

2.  уравнение колебаний шара, также это знаменитое уравнение Шрёдингера. Оно определено в комплексной плоскости, поэтому может описывать наряду с выраженными необратимыми процессами также колебания и распространение волн.

3.  уравнение линейных колебаний. Оно описывает циклические обратимые волновые процессы.

4.  уравнение нелинейных колебаний или уравнение Кортвега де Вриза (это уравнение описывает солитон, или одиночную волну несимметричной формы).

Примеры солитонов: цунами, нагонная волна, автоволны в солнечной плазме .

плотина

Уровень воды

Схема образования нагона волны: скорость волн на поверхности воды пропорционально глубине водоёма. Если уровень воды поднимается выше плотины, она может разрушиться. При этом вода начинает прорываться через плотину, образуя за плотиной водоём небольшой глубины. Движение воды возбуждает волны в основном водоёме, скорость которых при приближении к малому водоёму резко падает, также уменьшается кинетическая энергия волн. Так как суммарная энергия волны должна сохраняться, то резко увеличивается уровень воды, т.е. потенциальная энергия волны. Образуется нагонная волна, высота которой может составлять несколько десятков метров.