Контрольная работа № 5

В задачах 401–420 найти общее решение (общий интеграл) дифференциальных уравнений первого порядка.

401. ху х/ = х2 + у2 402. y/ = 403. ху/ + х tg = y 404. xy/ + y ln 405. y/ = + sin 406. 4xyy/ - y2 – 3x2 = 0 407. (x – y) y/ = 2x + y 408. xy/ = y + 409. xy/ ln = x + y ln 410. y/ =

411. y/ = 412. y/ = - tg 413. x2y/ = y2 + xy + x2 414. xy/ - y + =0 415. y/ = + 416. y/ = 417. xy/ = y + 3x sin 418. 2x2y/ + x2 + y2 = 0 419. (3x + y)y/ = x + 3y 420. xyy/ = 8x2 + y2

Решение типового примера. Найти общее решение (общий интеграл) дифференциального уравнения .

Решение. Правая часть уравнения обладает свойством . Поэтому заданное уравнение является однородным дифференциальным уравнением первого порядка. Совершим замену , где u – некоторая функция от аргумента х. Отсюда , . Исходное уравнение приобретает вид

.

Продолжаем преобразования:

;

.

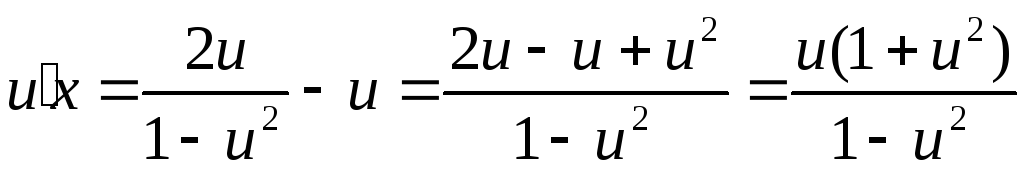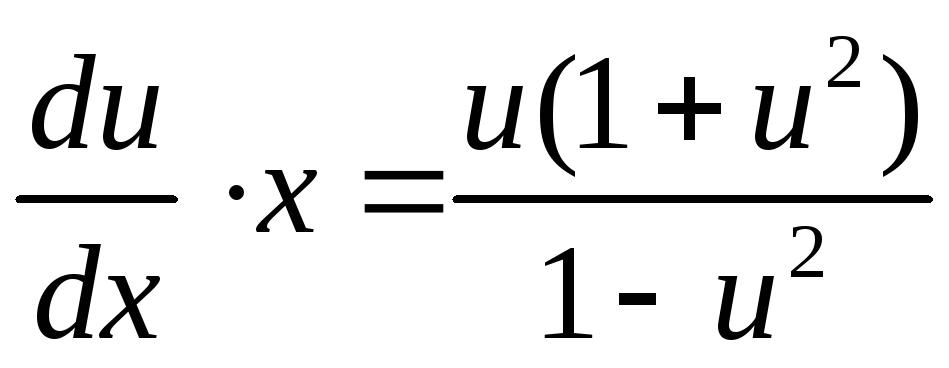Производим разделение переменных:

.

После интегрирования обеих частей уравнения получаем

;

.

Таким образом,

;

.

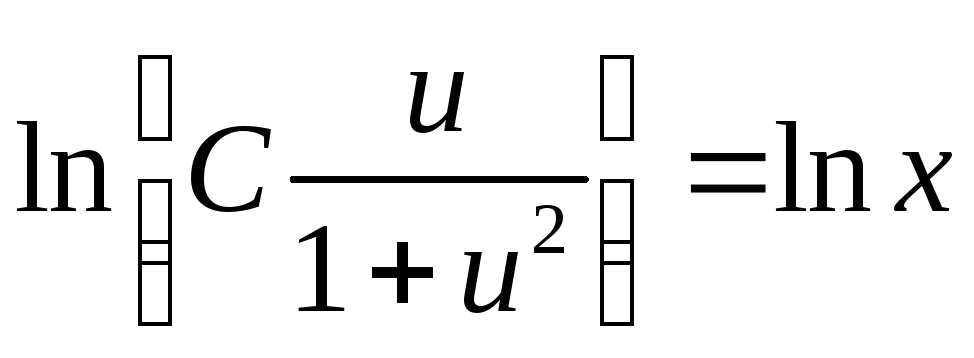Потенцируя, находим

или

.

Итак, общий интеграл исходного уравнения приобретает вид

,

где С – произвольная постоянная.

В задачах 421 – 440 найти частное решение дифференциального уравнения, удовлетворяющее указанному начальному условию.

421. xy/ - y = y2sin x, y 422. y/cos2x + y = tg x, y(0) = -1 423. y/ - y ctg x = , y= 0 424. (1 + x2) y/ + y = arctg x, y(0) = 1 425. y/ cos 2x + y = tg x, y (0) = -1 426. y/ + y = arcsin/x; y(0) = -1 427. (1 + x2)y/ + y = y2 arctg x, y(0) = 1 428. y/ + 2y tg 2x = sin 4x; y(0) = 0 429. xy/ - y = x2 cos x, y 430. y/ + y = e2xy2; y(0) = 2

431., y(0)=-1 432. xy/ - y = x2 cos x; y() = 433. y/ + 3ytg3x = sin6x, y(0) = 434. xy/ + y = -x2y2; y(1) = 1 435. y/ - , y(0) = 1 436. y/sin x = - y cos x = 1; y() = 0 437. y/ + y=x2y2, y(1) = 1 438. y/x + 2y = 3x5y2; y(1) = -1 439. y/ cos2x + y = y2 tg x, y(0) = -1 440. y/ + 2xy = 3x2e; y(0) = 0

Решение типового примера. Найти частное решение дифференциального уравнения , удовлетворяющее начальному условию .

Решение. Заданное дифференциальное уравнение является уравнением Бернулли. Полагаем , где – неизвестные функции от х, . Подставляя у и в исходное уравнение, будем иметь

,

Подберем функцию так, чтобы выражение, содержащееся в квадратной скобке, обращалось в нуль. Для определения имеем дифференциальное уравнение с разделяющимися переменными , откуда после интегрирования получаем , т.е.

.

Для определения функции имеем

или

.

Это дифференциальное уравнение с разделяющимися переменными относительно неизвестной функции . Разделяя переменные, будем иметь

.

Интегрируя обе части равенства, получаем

.

Последний интеграл вычисляем методом интегрирования по частям, в результате чего имеем

,

откуда

.

Таким образом, общее решение исходного уравнения имеет вид

.

Используя начальное условие, вычисляем соответствующее ему значение постоянной С:

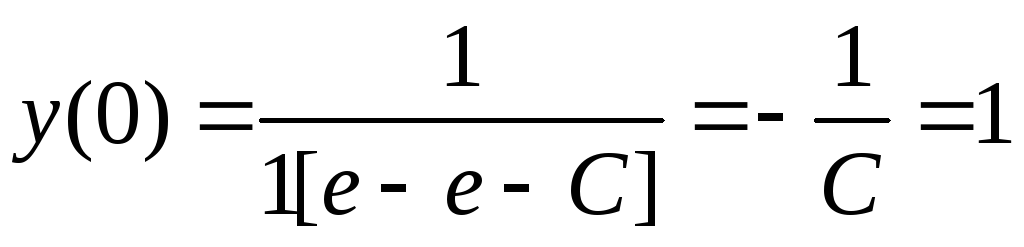, т. е. С = – 1.

Поэтому частное решение исходного дифференциального уравнения, удовлетворяющее заданному начальному условию, имеет вид

.

В задачах 441–460 найти: а) частное решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям; б) общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.

441. a) y// + 2y/ + 10y = 0; y= 0; y/= 1 б) y// - 5y/ + 6y = 2x e-x 442. a) xy// - y/ - x2 = 0; y(1) = ; y/(1) = 3 б) y// - 2y/ - 8y = 16x2 + 2 443. a) y// + 8y/ + 7y = 0; y(0) = 2; y/(0) = 1 б) y// - 6y/ + 8y = 3 e4x 444. a) y// - 3y/ - 9y = 0; y(1) = ; y/(1) = 1 б) y// - 4y/ + 3y = 8e5x 445. a) y// - 7y/ + 12y = 0; y(0) = 2; y/(0) = -2 б) y// + y/ - 2y = (x + 2) e-2x 446. a) y// + 4y/ + 4y = 0; y(0) = -2; y/(0) = -2 y// + 6y/ + 9y = 7 cos 3x 447. a) y// - 3y/ + 2y = 0; y(0) = 0; y/(0) = 1 б) y// + 7y/ = 2x2 + x 448. a) y// - 6y/ + 9y = 0; y(0) = 2; y/(0) = б) y// + 6y + 9y = 2e-3x 449. a) y// - 2y/ + 5y = 0; y(0) = -1; y/(0) = 0 б) y// + 3y/ - 10y = 2x2 ex 450. a) y// - 4y/ + 5y = 0; y(0) = 2; y/(0) = - б) y// + 2y/ + y = 2x + 1

451. a) y// + 10y/ + 25y = 0; y(0) = 1; y/(0)= 1 б) y// - 5y/ - 24y = (2x + 3) ex 452. a) y// + y/ - 6y = 0; y(0) = 0; y/(0) = 1 б) y// - 2y/ = 6x - 2 453. a) y// - 4y/ + 4y = 0; y(0) = 1; y/(0) = 3 б) y// + 2y/ - 3y = -2 e3x 454. a) y// - 4y/ + 3y = 0; y(0) = 3; y/(0) = y// + 16y/ + 64y = xe3x 455. a) y// - 4y/ + 17y = 0; y= 0; y/= 1 б) y// + 4y/ + 3y = -x e-x 456. a) y// - 5y/ +6y = 0; y(0) = 3; y/(0) = б) y// - 4y/ + 5y = 5x - 4 457. a) y// + y/ = 0; y() = -1; y/()= -4 б) y// + y/ - 6y = 2(x – 1) e-x 458. a) y// - 4y/ +4y = 0; y(0) = 3; y/(0) = б) y// - 4y/ + 5y = 5x - 4 459. a) y// + 8y/ + 16y = 0; y(0) = 1; y/(0) = 0 б) y// - 5y/ + 6y = 2x e3x 460. a) y// + 2y/ - 8y = 0; y(0) = -1; y/(0) = б) y// - y/ - 6y = 6x2 – 4x

Решение типовых примеров.

а) Найти частные решения следующих дифференциальных уравнений второго порядка при заданных начальных условиях:

1. ;

2. ;

3. .

Решение

1. Характеристическое уравнение

имеет два различных вещественных корня , поэтому общее решение этого дифференциального уравнения записывается в виде

,

где С₁, С₂ – произвольные постоянные. Отсюда

,

поэтому, основываясь на начальных условиях, получаем

, т. е. С₁ + С₂ = 1,

, т. е. 2С₁ + 4С₂ = 2.

Решая систему уравнений

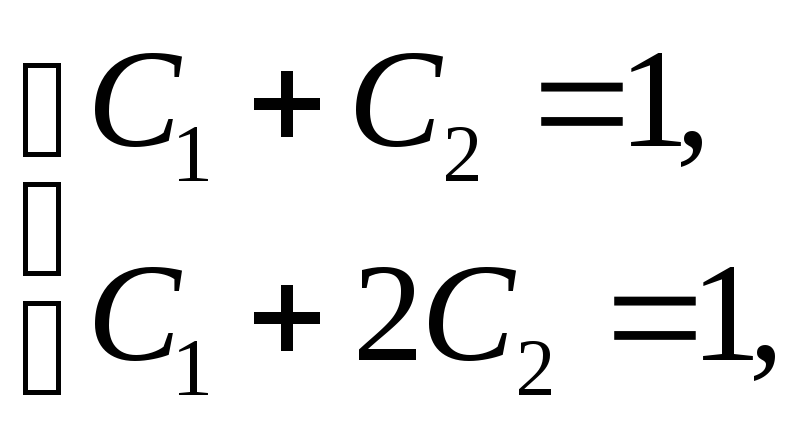
получаем С₁ = 1; С₂ = 0. Частное решение исходного уравнения, удовлетворяющее заданным начальным условиям, приобретает вид

.

2. Характеристическое уравнение

имеет два равных корня , поэтому общее решение соответствующего дифференциального уравнения записывается в виде

,

откуда

.

Учитывая начальные условия, получаем систему уравнений для определения С₁, С₂:

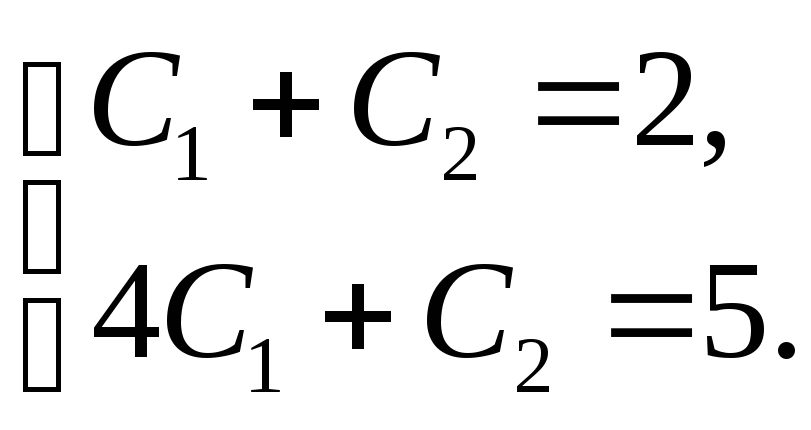
Отсюда С₁ = 1; С₂ = 1 поэтому искомое частное решение имеет вид

.

3. Характеристическое уравнение

не имеет вещественных корней. В этом случае общее решение соответствующего дифференциального уравнения записывается в виде

,

где ; (p, q – коэффициенты характеристического уравнения).

У нас α = 2; β = 3, поэтому общее решение заданного дифференциального уравнения имеет вид

Отсюда .

Таким образом, для определения значений С₁, С₂ исходя из начальных условий, получаем систему уравнений

Решая которую имеем С₁ = 0; С₂ = .

Итак, искомое частное решение приобретает вид

.

б) Найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами

.

Решение. Найдем общее решение Y однородного уравнения с теми же коэффициентами, что и в левой части заданного уравнения:

.

Так как корни его характеристического уравнения

действительны и различны (), то общее решение однородного уравнения записывается в виде

,

где С₁, С₂ – произвольные постоянные.

Подбираем теперь частное решение исходного неоднородного уравнения в виде

.

Отсюда

,

.

Подставляя в исходное уравнение и сокращая все слагаемые на множитель получаем

или после упрощения

.

Отсюда следуют равенства , т. е. .

Таким образом, общее решение заданного неоднородного дифференциального уравнения имеет вид

.

В задачах 461 – 480: а) исследовать на сходимость с помощью признака Даламбера знакоположительный ряд; б) исследовать на сходимость с помощью признака Лейбница знакочередующийся ряд; в) найти радиус сходимости степенного ряда и определить тип сходимости ряда на концах интервала сходимости.

Решение типовых примеров.

а) Исследовать на сходимость с помощью признака Даламбера знакоположительный ряд

.

Решение. Общий член ряда

.

Тогда . В соответствии с признаком Даламбера вычислим предел

.

Так как d < 1, делаем вывод о сходимости заданного ряда.

б) С помощью признака Лейбница исследовать сходимость знакочередующегося ряда

Решение. Рассмотрим абсолютные величины членов исходного ряда:

.

При этом 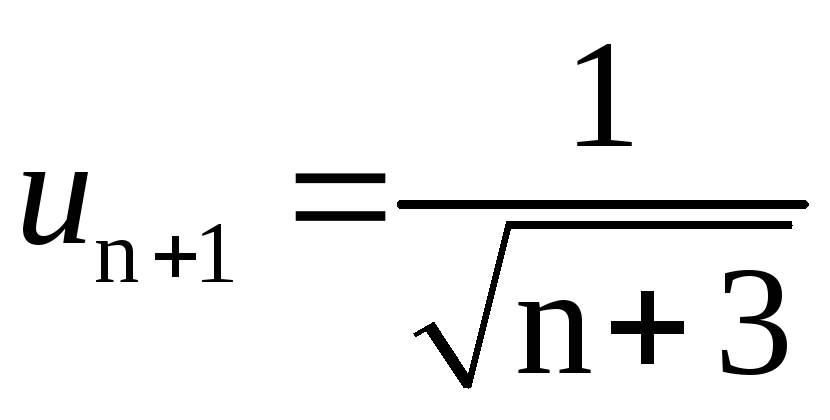и или .

Таким образом, члены заданного ряда монотонно убывают по абсолютной величине. Кроме того . Поэтому выполнены оба условия признака Лейбница, т. е. ряд сходится.

в) Найти радиус сходимости степенного ряда

.

Определить характер сходимости ряда на концах интервала сходимости.

Решение. Запишем заданный ряд следующим образом:

Общий член ряда .

Для исследования ряда на абсолютную сходимость применим признак Даламбера:

.

Таким образом, при т. е. при исходный ряд сходится абсолютно.

Выясним вопрос о сходимости ряда на концах интервала сходимости, т.е. в точках х = – 7, х = 7. При х = – 7 заданный ряд принимает вид

.

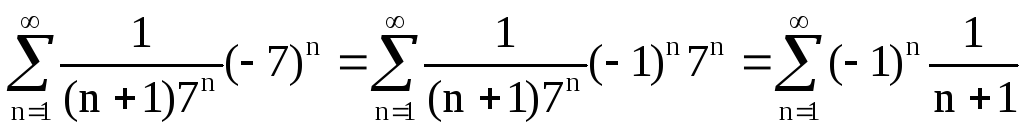Это числовой знакочередующийся ряд. Его общий член по абсолютной величине монотонно убывает и стремится к нулю при . Таким образом, оба условия признака Лейбница выполнены и ряд сходится (условно), т. е. точка х = – 7 принадлежит области сходимости заданного степенного ряда.

При х = 7 исходный ряд принимает вид

Это числовой знакоположительный ряд, который, очевидно расходится (сравните его с гармоническим рядом). Следовательно, точка х = 7 не принадлежит области сходимости заданного степенного ряда.

Таким образом, область сходимости исходного степенного ряда . Вне этого интервала ряд расходится.

В задачах 481 – 500 вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.

Решение типового примера. Вычислить с точностью до 0,001 интеграл

путем предварительного разложения подынтегральной функции в степенной ряд и почленного интегрирования этого ряда.

Решение. В разложении функции в степенной ряд

Заменим х на – х². Тогда получим

Умножая этот ряд почленно на х² будем иметь

Следовательно,

.

Полученный знакочередующийся ряд удовлетворяет условиям признака Лейбница. Третий член этого ряда по абсолютной величине меньше 0,001, поэтому для обеспечения требуемой точности нужно просуммировать первые два члена ряда.

Итак,

.

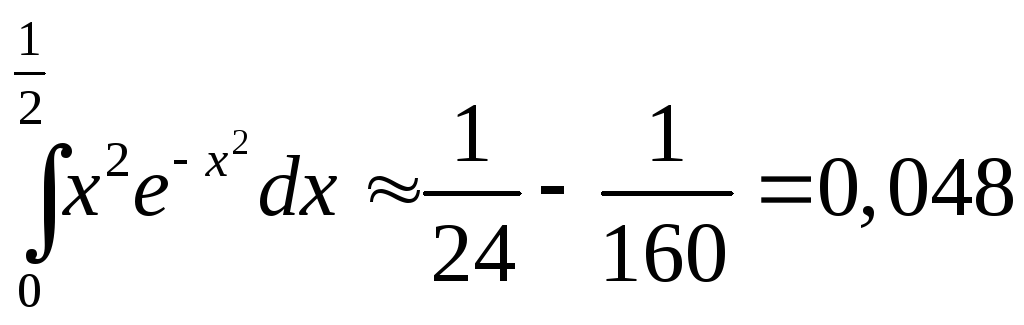В задачах 501 – 520 разложить заданную функцию в ряд Фурье по косинусам на отрезке .

501.	511.
502.	512.
503.	513.
504.	514.
505.	515.
506.	516.
507.	517.
508.	518.
509.	519.
510.	520.

Решение типового примера. Разложить функцию в ряд Фурье по косинусам на отрезке .

Решение. Так как по условию ряд должен содержать только косинусы кратных дуг, то следует продолжить заданную функцию на отрезок четным образом. Для определения коэффициентов ряда Фурье применяем формулы

,

.

Отсюда

,

.

Последний интеграл вычисляем методом интегрирования по частям, полагая . Отсюда .

Следовательно,

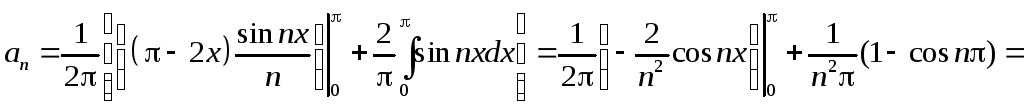
Таким образом, искомое разложение имеет вид

.
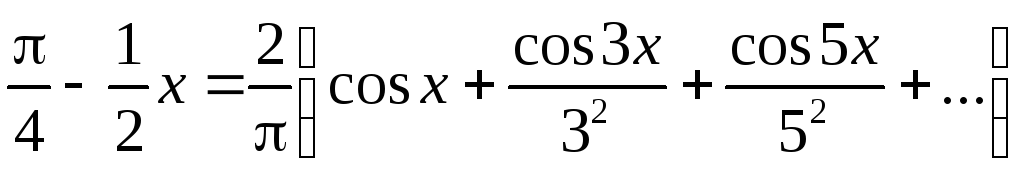