Контрольная работа № 4

В задачах 301‑310 вычислить частные производные первого и второго порядков от заданных функций.

301. z= 8 ln (xy²) + 10xy² + 8x.

302. z= 2 tg (xy) – 7x²y + 6x.

303. z= 8 cos (xy) – 3x – 12x⁴y.

304. z= 3 ctg (x²y) + 7y – 6xy².

305. z= x sin (xy) + 8x²y² – 7x.

306. z= 6e+ 3(x² + y²) + 3.

307. z= +3x⁴y – 8x – 2.

308. z= 9e- 5xy³ – 3y + 2.

309. z= 8 ln (x² + y²) – 6x²y³ + 8x – 1.

310. z= 3 - 4y²x + 3y - 2.

Решение типового примера. Пусть .

При вычислении частной производной переменную рассматриваем как постоянную величину. Пользуясь правилом дифференцирования функции одного аргумента и, в частности, правилом дифференцирования сложной функции, получаем

Аналогично поступаем при вычислении Считая постоянной величиной, получаем

Используя те же правила, вычисляем частные производные второго порядка:

В задачах 311 – 320 задана функция z = f(x, y). Найти градиент и производную этой функции в заданной точке М(х₀, у₀) в направлении вектора , составляющего угол с положительным направлением оси Ох.

311. z= tg x + x – 2 sin y, M(), =.

312 z= , M(1; -1), =.

313. z= 2 cos (x +y) +2x, M(), =.

314. z= 3 tg x – 2x cos y, M(;);=.

315. z= ln (x² + y²), M(3, 4), =.

316. z= x sin(x+y) – 1, M(;), =.

317. z= x tg y + cos x, M(),=.

318. z= 2x² + 3xy + y², M(2; 1), =.

319. z= , M(2,2), =.

320. z= 5x² + 6xy, M(2; 1), =.

Решение типового примера. Пусть z = 2 tg x – 3x cos y.

Найдем градиент и производную этой функции в точке М в направлении, составляющем угол с положительным направлением оси Ох. Для этого вычислим частные производные функции:

Вычислим теперь значения этих производных в точке М :

Таким образом,

(grad z)_M = .

Производная в направлении вектора , составляющего угол с положительным направлением оси Ох, вычисляется по формуле

,

т.е. в нашем случае

.

В задачах 321 – 340 найти экстремум заданной функции.

321. z= 2x² – xy + y² – 3x – y + 1.

322. z= x² + 2xy – y² + 4x.

323. z= 2x² + xy – y² – 7x + 5x + 2.

324. z= x² + y² = 9xy + 27.

325. z= 3x² + xy – 6y² – 6x – y + 9.

326. z= 5x² – 3xy + y² + 4.

327. z= 4x² – 2xy + y² – 2x – 4y + 1.

328. z= x² + 3y² + x - y.

329. z= 8x² – xy + 2y² – 16x + y – 1 .

330. z= 3 – 2x² – xy – y².

331. z= 6xy – 2x² – y² – 14x + 5.

332. z= 3xy – x² – 3y² – 6x + 9y - 4.

333. z= 10xy – 3x² – 2y² – 26x + 18y – 1.

334. z= x² + y² – xy + x + y +2.

335. z= 3 – 3x² + 5y² – 8xy + 4x + 26y.

336. z= 3x² + 3y² + 5xy + x – y + 5.

337. z= 5x² – 3x² + 2xy – 18x – 10y + 4.

338. z= x² + 2xy – y² + 6x – 10y + 1.

339. z= 2x² – 3y² + 2xy – 10x + 16y – 7 .

340. z= 4 – 5x² – y² – 4xy + 4x – 2y.

Решение типового примера. Пусть

z = 2x² – xy + 3y² – 2x – 11y + 1.

Находим частные производные функции:

Воспользовавшись необходимыми условиями экстремума, находим стационарные точки. Для этого решаем систему уравнений

откуда х = 1; у = 2. Таким образом, стационарной является точка М (1, 2).

Находим значения частных производных второго порядка в точке М:

Составляем выражение

Так как и , делаем вывод о наличии минимума в точке М (1, 2). При этом минимальное значение функции равно z_min = -11.

В задачах 341 – 360 с помощью двойного интеграла вычислить координаты центра тяжести фигуры, ограниченной заданными линиями (поверхностную плотность считать равной единице).

341. x² + 4y² = 1; -x + 2y = 1.

342. x² + y² = 16; x + y = 4.

343. x² + y² = 9; x + y – 3 = 0.

344. .

345. x² + 25y² = 1; x – 5y = 1.

346. 16x² + 25y² = 1; 4x – 5y = 1.

347. 4x² + 25y² = 1; 2x – 5y – 1 = 0.

348. 4x² + 9y² = 1; 2x – 3y – 1 = 0.

349. x² + y² = 4; x + y + 2 = 0.

350. 9x² + 25y² = 1; 3x + 5y – 1 = 0.

351. y² = 2x + 4; y² = -x + 1.

352. y² = 3x – 2; y² = -x + 1.

353. y² = 9x + 9; y² = -x + 9.

354. y² = 4x + 4; y² = -x + 4.

355. x² = 2y + 4; x² = -y + 4.

356. x² = y + 2; x² = -y + 2.

357. x² = 3y + 9; x² = -y + 9.

358. x² = 3y + 7; x² = -y + 7.

359. x² = 25y + 25; x² = 5y + 25.

360. x² = 16y + 4; x² = 4y + 4.

Решение типовых примеров.

Пример 1. Найти координаты центра тяжести фигуры, ограниченной эллипсом и прямой (поверхностную плотность в каждой точке считать равной единице).

Решение. В случае однородной пластины, занимающей область D плоскости хОу, координаты центра тяжести находят по формулам:

где S – площадь области D,

.

В рассматриваемом случае (см. рис. 7) фигура ограничена кривыми у = и у = 3(1 - ) при . Поэтому

S =

=

Рис. 7

Для вычисления полученного интеграла используем замену . При этом . Отсюда

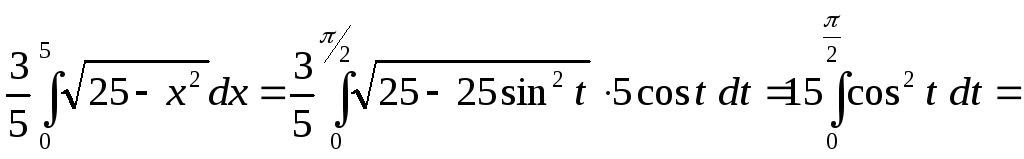
Итак, Далее

Первый из полученных интегралов вычисляется с помощью замены . Тогда и

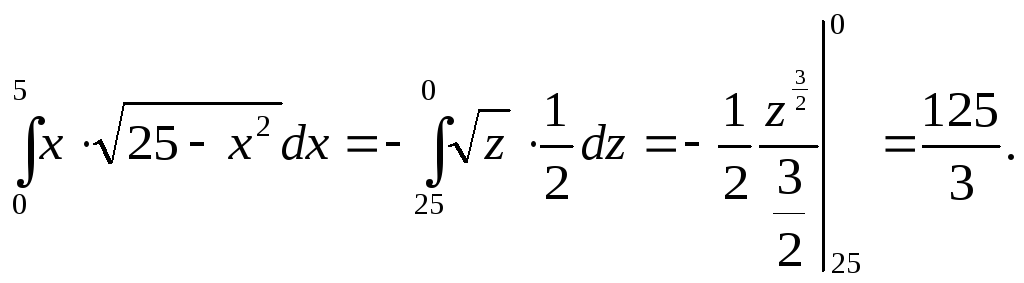
Отсюда

Наконец,

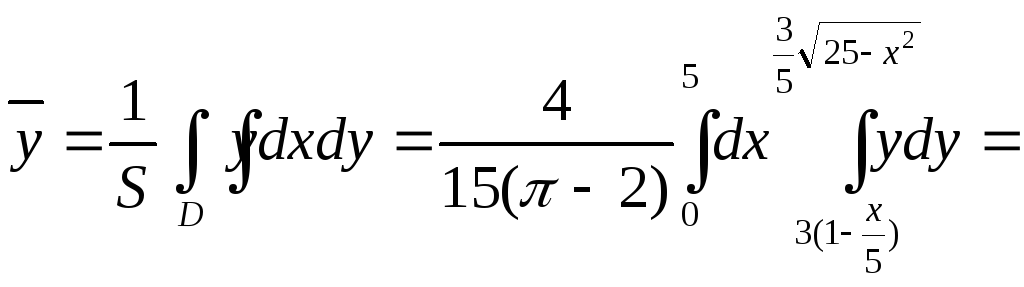
Пример 2. Найти координаты центра тяжести фигуры, ограниченной линиями у² = х + 9, у² = -3х + 9 (рис. 8) ( поверхностную плотность считать равной единице).

Решение.

Рис.8

Поскольку фигура симметрична относительно оси Ох, то = 0. Вычислим первую координату центра тяжести

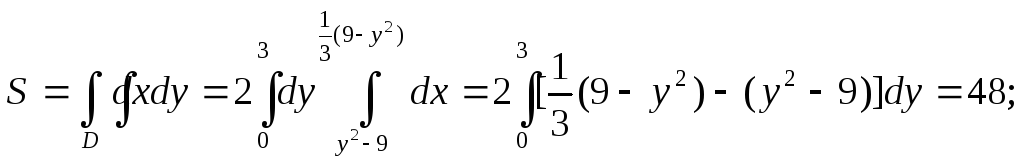
Таким образом, , = 0.

В задачах 361–380 вычислить объем тела, ограниченного заданными поверхностями и расположенного в первом октанте.

361. x² + y² + z² = 16; x² + y² = 4.

362. z = 2x + y; y =; x = 0; y = 0; z = 0.

363. x² + y² = 2; x + y + z = 2; z = 0.

364. z = 3x; y = ; y = 0; z = 0.

365. x² + y² = ; x + y + z = 1; z = 0.

366. z = x² + y² + 1; x + y = 3; x = 0; y = 0; z = 0.

367. x² + y² + z² = 36; z = 0; y = x; y = 0.

368. z = 6 – x – y; 2x + y = 4; x = 0; y = 0; z = 0.

369. x² + y² = ; x + y + z = 3; z = 0.

370. y = ; z= 3x + 2y; x = 0; y = 0; z = 0.

371. x² + y² = 5; z = x² + y^2.

372. 4x + 3y – 12 = 0; z = x² + 1; x = 0; y = 0; z = 0.

373. x² + y² = 18; x + y + z = 6; z = 0.

374. z = x + y + 2; y = 2x: x = 3; x = 0; y = 0; z = 0.

375. z = 8 - x² - y²; x² + y² = 3; y = x; y = 0.

376. x + y = 1; z = 9x² + 3y² + 2; x = 0; y = 0; z = 0.

377. z = 1 - x² - y²; y = x; y = ; z = 0.

378. x + 2y = 2; z = 8 – 2x² + 4y; x = 0; y = 0; z = 0.

379. x² + y² = 18; y = x; y = 0; x + y + z = 6; z =0.

380. x² + y² + z² = 4; x² + y² = 3.

Решение типовых примеров.

Пример 1. Вычислить объем тела, ограниченного поверхностями х² + у² = 8, х =0; у = 0; z = 0; х + у + z = 4 и расположенного в первом октанте.

Решение. Заданное тело ограничено круговым цилиндром х² + у² = 8, координатными плоскостями и плоскостью х + у + z = 4.

Объем цилиндрического тела, ограниченного сверху поверхностью z = f(x,y), снизу плоскостью z = 0 и по бокам прямой цилиндрической поверхностью, вырезающей на плоскости хОу область D, вычисляется по формуле

V =

В данном случае область D – это область круга радиуса , расположенная в первом квадранте, поэтому рассматриваемый интеграл удобно вычислять в полярных координатах. При этом , , . Таким образом,

Пример 2. Найти объем тела, ограниченного поверхностями х²+у² = 9; х²+z² = 9 и расположенного в первом квадранте.

Решение. Заданное тело ограничено двумя круговыми цилиндрами.

Искомый объем выражается интегралом

,

где D – четверть круга радиуса, равного 3.

Таким образом,

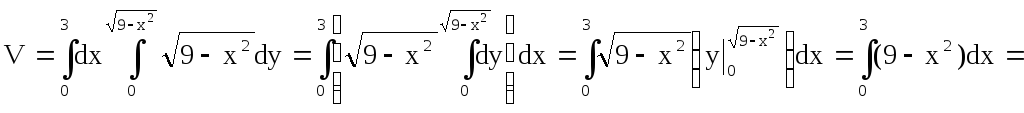
В задачах 381–390 вычислить работу, совершаемую переменной силой на криволинейном пути L, соединяющем заданные точки М и N.

381.

L – дуга параболы y = 2x² + 1; M (0;1), N (2;9)

382.

L – дуга параболы y = 2x³ + 1; M (1;3), N (2;10)

383.

L – дуга параболы y = 7x² +2х; M (0;0), N (2;32)

384.

L – дуга параболы y = 3x² + х; M (1;3), N (2;25)

385.

L – дуга параболы y = 3x² + х; M (1;4), N (3;30)

386.

L – отрезок прямой, соединяющий точки M (1;2), N (4;6)

387.

L – дуга кубической параболы y = x³+1; M (1;3), N (2;10)

388.

L – дуга параболы y = x³ ; M (0;1), N (3;3)

389.

L – дуга параболы y = 3x² + 2; M (2;14), N (3;29)

390.

L – дуга параболы y = 2x² ; M (1;2), N (3;10)

Решение типового примера. Вычислим работу, совершаемую переменой силой на дуге параболы у = 3х² + х, соединяющей точки М (1; 4) и N (3; 29). Для этого необходимо вычислить криволинейный интеграл

.

Преобразуем этот криволинейный интеграл к определенному интегралу, для чего вычислим дифференциал и заметим, что переменная изменяется в пределах от х₁ = 1 до х₂ = 2. Тогда

.

В задачах 391–400 установить независимость от пути интегрирования и вычислить криволинейный интеграл по контуру, связывающему точки М(1;2) и N(3;5).

391. .

392. .

393..

394. .

395..

396. .

397. .

398. .

399..

400. .

Решение типового примера. Вычислим криволинейный интеграл

по контуру, соединяющему точки М(1;1) и N(2;30), предварительно убедившись в независимости его от пути интегрирования.

В данном случае выполнено условие независимости криволинейного интеграла от пути интегрирования

,

где Р = х² + 3ху, Q = . Действительно, , .

Выберем в качестве контура интегрирования наиболее простой контур, связывающий точки М и N, например, ломанную, звенья которой параллельны осям координат:

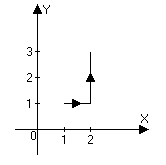
Рис. 9

Имеем на первом участке у =1, dy =0, 1 х 2; на втором участке х = 2, dx = 0, 1 у 3.

Таким образом,

.