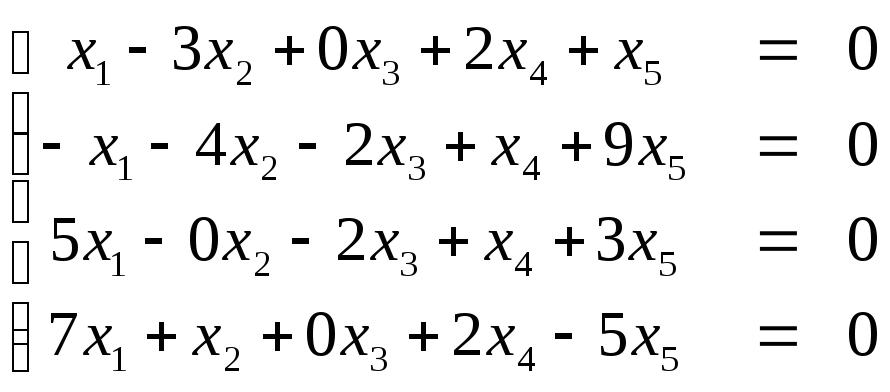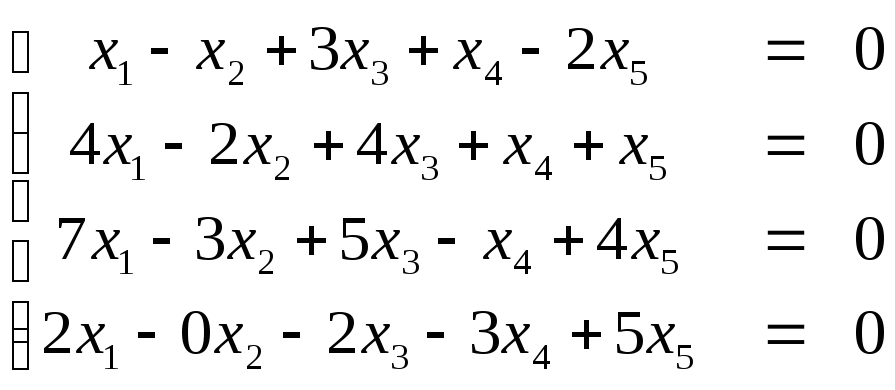- •Оглавление
- •Матрицы
- •Решение систем линейных уравнений
- •Векторные пространства
- •Квадратичные формы
- •1. Матрицы
- •Основные понятия и операции над матрицами
- •1.2. Определитель квадратной матрицы
- •1.3. Обратная матрица
- •1.4. Решение простейших матричных уравнений
- •1.5. Ранг матрицы
- •Упражнения для самостоятельного решения
- •2.Решение систем линейных уравнений
- •Формулы Крамера
- •Метод Гаусса
- •Исследование произвольных линейных систем уравнений
- •3. Векторные пространства
- •3.1. Линейные векторные пространства
- •Линейная зависимость и независимость векторов
- •Упражнения для самостоятельного решения
- •Размерность и базис пространства векторов
- •Ранг системы векторов
- •Задачи для самостоятельного решения
- •3.5. Пространство решений однородной системы уравнений
- •Задачи для самостоятельного решения
- •3.6. Общее решение неоднородной системы линейных алгебраических уравнений
- •Переход к новому базису
- •3.8. Евклидово пространство
- •Линейные преобразования и линейные операторы
- •Матрица линейного преобразования
- •Изменение матрицы линейного преобразования при переходе к новому базису
- •Собственные векторы и собственные значения линейного оператора
- •Ортогональные и симметрические матрицы линейных преобразований
- •Квадратичные формы
- •Матрица квадратичной формы
- •Канонический вид квадратичной формы
- •Индивидуальные задания для студентов по теме « Линейная алгебра».
- •1. Вычислить, используя свойства определителя.
- •3. Выбрать пары матриц, которые можно перемножить, и выполнить умножение.
- •4. Решить матричное уравнение.
- •5.Найти ранг матрицы
- •7. Исследовать систему на совместность, написать множество решений.
- •8. Проверить, образуют ли векторы е1, е2, е3 ортогональный базис, и найти разложение вектора х по этому базису.
- •9. Определить, является ли система векторов линейно зависимой.
- •10. Найти фундаментальную систему решений системы уравнений
- •11. Найти собственные значения и собственные векторы матрицы
- •Литература
9. Определить, является ли система векторов линейно зависимой.
|
Вар. |
Векторы |
Вар |
Векторы |
|
1 |
Х1=(-1, 1,1), X2=(4, 1,-2), X3=(0, -1, 2). |
2 |
Х1=(1,-1, 2), X2=(3, -1, -8), X3=(-1, 0,5). |
|
3 |
Х1=(2, 1,0), X2=(-5, 0, 5), X3=(1, 4, 3) |
4 |
Х1=(5, 3, 0), X2=(-1, -6, -1), X3=(0,-1, 1) |
|
5 |
Х1=(5, -6,1), X2=(3,-5, -3), X3=(0, -1, 3) |
6 |
Х1=(6, 3, 1), X2=(0, -3, 0), X3=(-3, -2, 0) |
|
7 |
Х1=(-6 -2, 1), X2=(3, -2, 1), X3=(0, 0, 3) |
8 |
Х1=(3,-1 ,2 ), X2=(-2,2 ,-3 ), X3=(1,3,4 ). |
|
9 |
Х1=(5,-1 ,1 ), X2=(5,3 ,2 ), X3=(9,-1 ,2 ). |
10 |
Х1=(2,5 ,2 ), X2=(1,1 ,1 ), X3=(1,3 ,2 ). |
|
11 |
Х1=(1,1 ,0 ), X2=(-1,2 ,0 ), X3=(0,3 ,-3 ). |
12 |
Х1=(-1,2 ,-1 ), X2=(0,2 ,-1), X3=(1,2 ,2 ). |
|
13 |
Х1=(2,0 ,-1), X2=(3,1,-3 ), X3=(1,-1 ,0 ). |
14 |
Х1=(0,2 ,-1 ), X2=(3,1 ,2 ), X3=(1,2 ,1 ). |
|
15 |
Х1=(-2,-7,6 ), X2=(-4,4 ,4), X3=(0,-2 ,3) |
16 |
Х1=(1,-2 ,3 ), X2=(5,-3 ,4 ), X3=(2,1 ,-2) |
|
17 |
Х1=(-7,0 ,7 ), X2=(1,3 ,1 ), X3=(-2,1 ,-1) |
18 |
Х1=(1,-1 ,0 ), X2=(0,2 ,-1 ), X3=(0,2 ,0 ). |
|
19 |
Х1=(8,0,-3 ), X2=(-1,-1 ,2), X3=(7,-1,-1) |
20 |
Х1=(1,-1 ,2 ), X2=(4,-7 ,12 ), X3=(-1,3,1) |
|
21 |
Х1=(1,2 ,1 ), X2=(2,-1 ,-1 ), X3=(1,1 ,2 ). |
22 |
Х1=(-3,-1 ,3 ), X2=(1,1 ,-1), X3=(-2,-1,2) |
|
23 |
Х1=(1,-1 ,4 ), X2=(3,3 ,-6 ), X3=(2,1 ,-1) |
24 |
Х1=(-1,-2 ,1 ), X2=(4,-1 ,1 ), X3=(2,0 ,2) |
|
25 |
Х1=(-3,-4 ,-7), X2=(1,-2 ,3 ), X3=(2,2 ,2) |
26 |
Х1=(0,-2 ,8 ), X2=(-1,2 ,-1), X3=(3,2 ,-1) |
|
27 |
Х1=(1,3 ,3 ), X2=(2,3 ,-2 ), X3=(0,-8 ,-1) |
28 |
Х1=(10,15 ,2), X2=(9,10 ,12), X3=(2,4,4) |
|
29 |
Х1=(2,3 ,2 ), X2=(2,2 ,3 ), X3=(-4,-3 ,-7) |
30 |
Х1=(1,3 ,3 ), X2=(2,4 ,1 ), X3=(1,2 ,3 ). |
10. Найти фундаментальную систему решений системы уравнений
|
Вар. |
Система уравнений |
Вар |
Система уравнений |
|
1 |
|
2 |
|
|
3 |
|
4 |
|
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
|
11 |
|
12 |
|
|
13 |
|
14 |
|
|
15 |
|
16 |
|
|
17 |
|
18 |
|
|
19 |
|
20 |
|
|
21 |
|
22 |
|
|
23 |
|
24 |
|
|
25 |
|
26 |
|
|
27 |
|
28 |
|
|
29 |
|
30 |
|