Задачи для самостоятельного решения

Найти ранг и базис системы векторов и один из векторов, не входящий в базис, разложить по базису.

1.

2.

3.

Ответы: 1. r=3; если базис (а₂, а₃, а₄), то

2. r=3; если базис (а₁ ,а₂, а₃), то

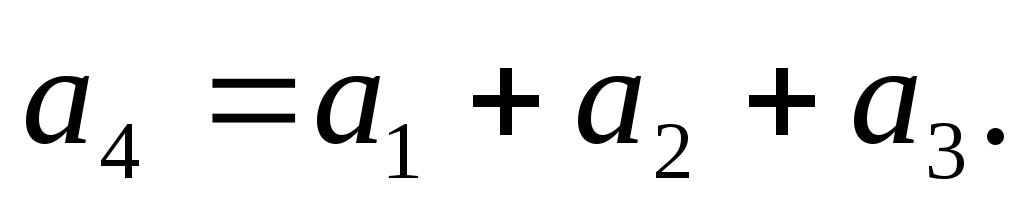
3. r=3; если базис (а₁ ,а₂, а₃), то

3.5. Пространство решений однородной системы уравнений

Однородной системой линейных алгебраических уравнений называется система вида

. В общем случае Эта система уравнений всегда совместна, так как имеет очевидное нулевое решение Поставим задачу отыскания ненулевых решений такой системы. В матричной форме система примет вид А·Х=0, где А=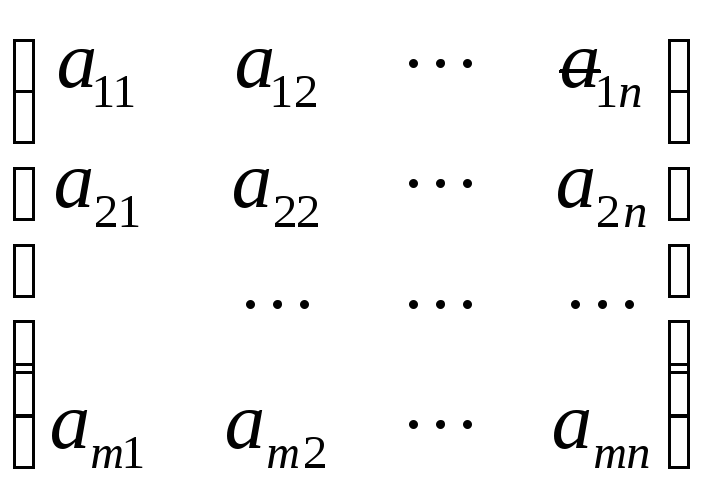 матрица системы уравнений, Х= - матрица неизвестных. Если матрица А квадратная (m=n) , и ранг матрица r=n, то система уравнений имеет единственное нулевое решение. Поэтому для существования ненулевого решения предположим, что r<m≤n. Тогда существует минор порядка r матрицы А, не равный нулю, пусть для определенности это будет минор

Исходная система уравнений может быть записана в виде

.

Данная система, очевидно, эквивалентна предыдущей. Назовем основными неизвестными, свободными неизвестными. Свободным неизвестным можно придавать любые числовые значения, кроме случая одновременного равенства всех свободных неизвестных нулю. Следовательно, последняя система имеет бесчисленное множество решений.

Множество решений однородной системы уравнений образует линейное векторное пространство. Действительно, если вектор является решением однородной системы уравнений, то вектор также является решением, что легко проверить, подставив компоненты вектора αх в систему.

Если векторы и являются решениями, то их сумма является решением данной однородной системы уравнений, что проверяется подстановкой компонентов вектора z в систему уравнений.

Найдем теперь размерность и базис пространства решений однородной системы уравнений. Количество свободных неизвестных равно n-r, придавая поочередно каждой свободной неизвестной значение, равное единице, а остальные приравнивая нулю, можно получить n-r векторов решений: при решая систему, получим вектор При получим вектор решения и так далее. Аналогично при решение будет Векторы линейно независимы, так как матрица С, составленная из компонентов этих векторов имеет ранг, равный к=n-r, то есть равен числу векторов. Матрица С=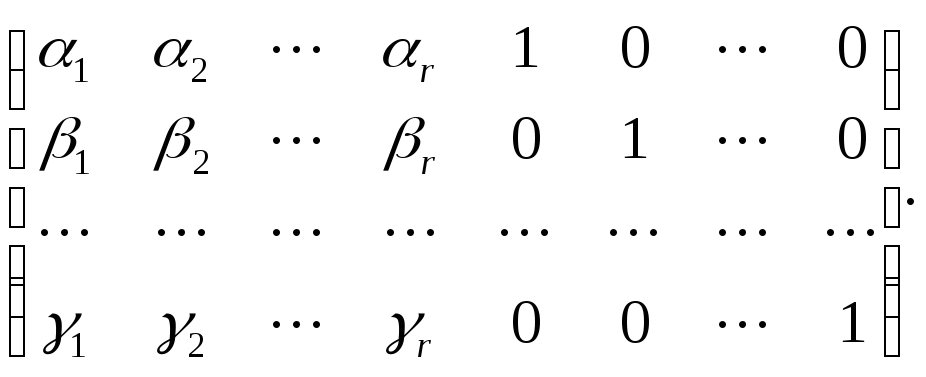

Векторы e₁, e_2,…..,e_k называются фундаментальной системой решений, они образуют базис пространства решений, размерность которого равна k = n – r . Любое другое решение будет линейной комбинацией базисных векторов. Поэтому можно записать общее решение однородной системы в виде где с₁, с₂, ……,с_к- произвольные действительные числа, одновременно не равные нулю.

Пример. Найти фундаментальную систему решений и размерность пространства решений однородной системы уравнений

.

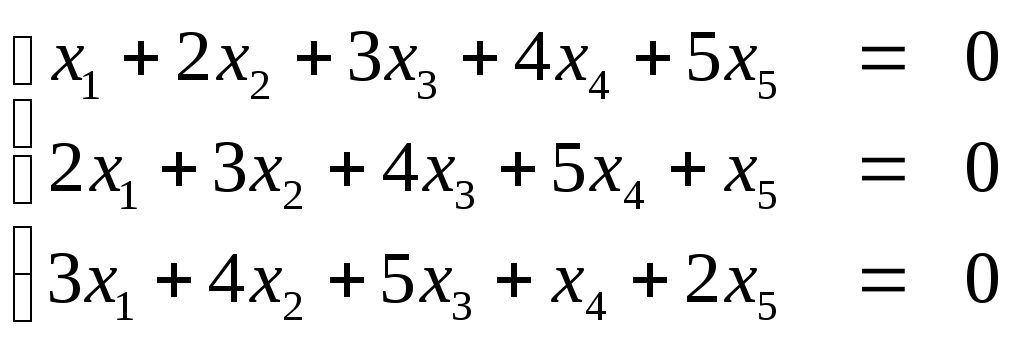Решение. Сначала найдем ранг матрицы А системы уравнений: А=. Умножим первую строку на два и вычтем из второй строки, затем умножим первую строку на три и вычтем из третьей строки, получим матрицу 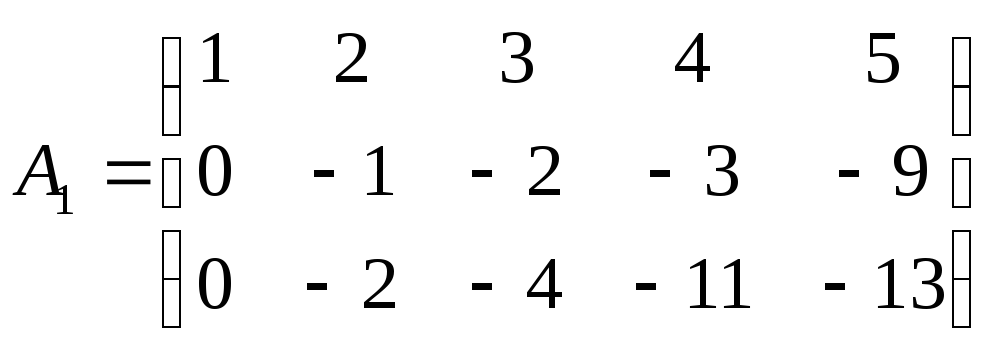. В матрице А₁ вторую строку умножим на (-2) и прибавим к третьей строке, получим матрицу А₂, в которой элементы второй строки запишем с противоположным знаком. Получим матрицу А₂= В матрице А₂ третью строку разделим на

(-5) и запишем матрицу А₃ =. Очевидно, что в А₃ базисный минор, составленный из элементов первого, второго и четвертого столбцов, третьего порядка и равен 1:

М₃ =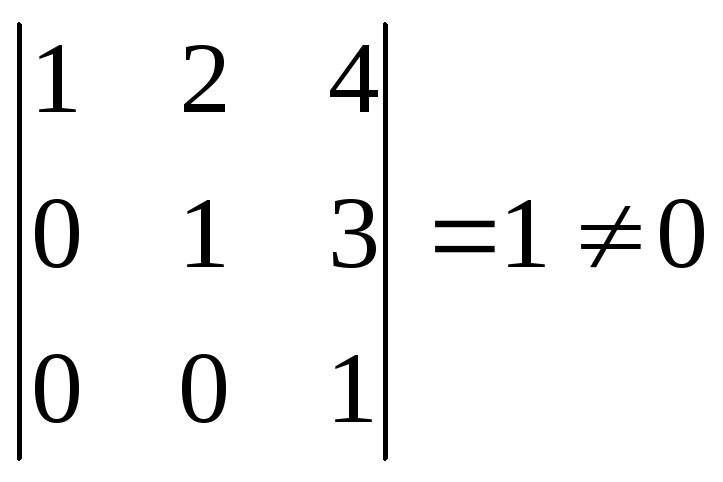. Следовательно, ранг матрицы А системы уравнений равен трем, ранг меньше числа неизвестных, что доказывает существование бесчисленного множества решений данной системы уравнений. За основные неизвестные возьмем х₁ ,х_{2 ,},х₄, а за свободные х₃ , х₅ . По последней матрице А₃ запишем систему уравнений в виде:

.

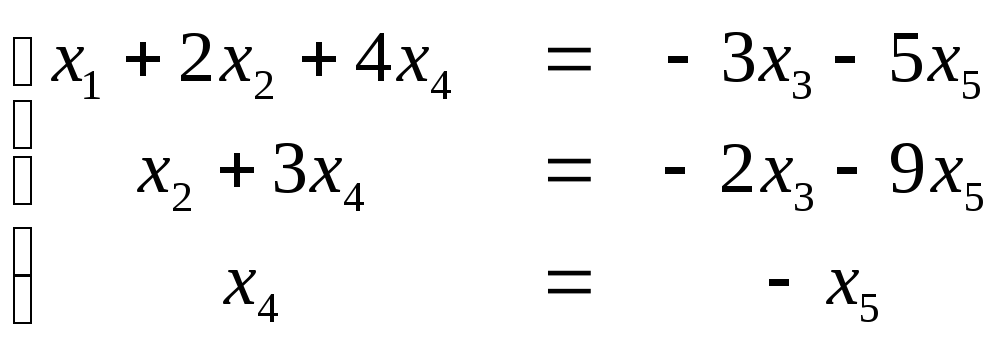1. Пусть х₃=1, х₅=0. Получим систему уравнений

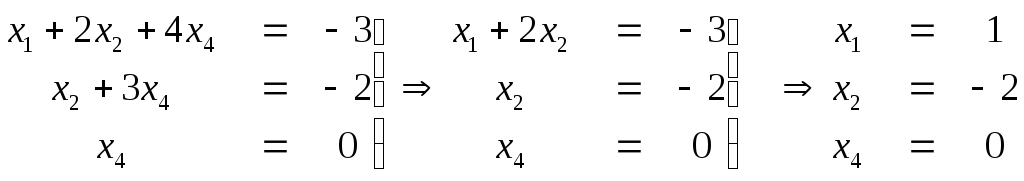Вектор решения е₁=(1,-2,1,0,0).

2. Пусть х₃=0, х₅=1, тогда система уравнений примет вид

Вектор решения е₂=(11,-6,0,-1,1). Векторы е₁, е₂ – фундаментальная система решений, образует базис пространства решений, размерность которого k=2. Пространство решений можно записать в виде общего решения где с₁ и с₂ - произвольные числа, одновременно не равные нулю.