4. Линейные преобразования и линейные операторы

1. Матрица линейного преобразования

Рассмотрим два линейных векторных пространства размерности n и размерности m. Пусть задана матрица чисел

А=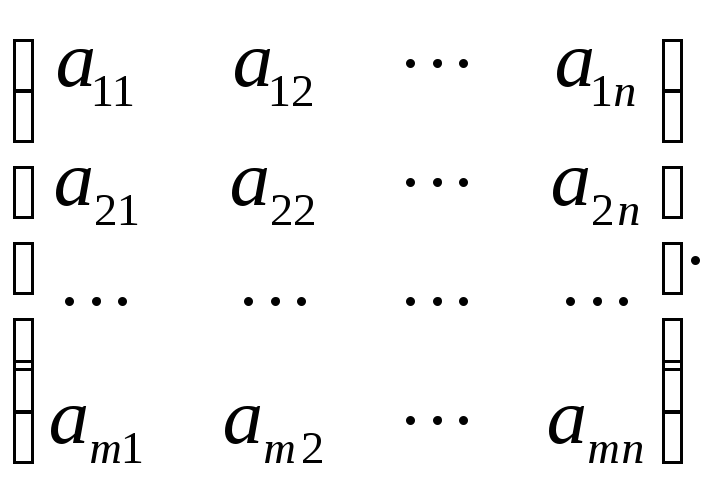

Если записать матричное равенство

Y=Ax (4.1.1)

где х=( х₁, х₂, …,х_п) то говорят, что задано линейное преобразование векторов. Матрица А называется линейным оператором, задающим отображение пространства

Выражение (4.1.1) через компоненты векторов имеет вид

( 4.1.2.)

Очевидно, что из (4.1.2) следует

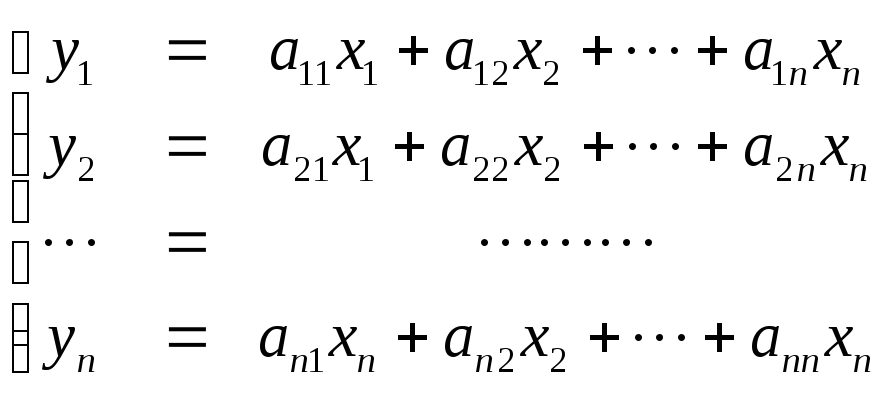(4.1.3)

Если матрица квадратная и невырожденная, то есть det (A)то вектор y=(y₁,y₂,…,y_n) будет принадлежать тому же пространству R_n. Тогда говорят, что оператор А отображает пространство R_n в себя. Такие операторы будем использовать в дальнейшем при изложении темы. Линейные операторы удовлетворяют следующим соотношениям:

1. А(х+у)=А(х)+А(у)

2. А(λх)=λА(х), где х,у 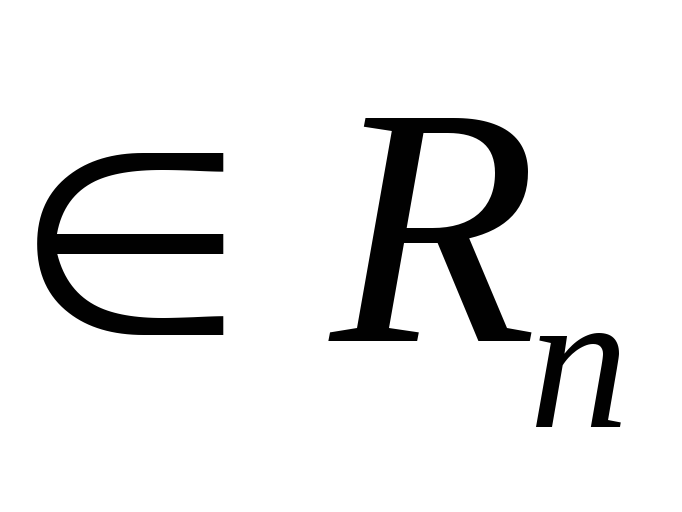,λ- действительное число.

3. (А+В)х=А(х)+В(х)

4. (АВ)х=А(В(х)), где матрицы А, В квадратные и одной и той же размерности. Существует нулевой оператор 0, переводящий все векторы пространства R_n в нулевые векторы 0х=0 и тождественный оператор Е, оставляющий вектор неизменным, т.е. Ех=х.

Пример. В пространстве R₃ в базисе е₁,е₂.е₃ линейный оператор задан матрицей А= Найти образ вектора х=е₁-2е₂+3е₃.

Решение. По формулам (4.1.2), (4.1.3) имеем

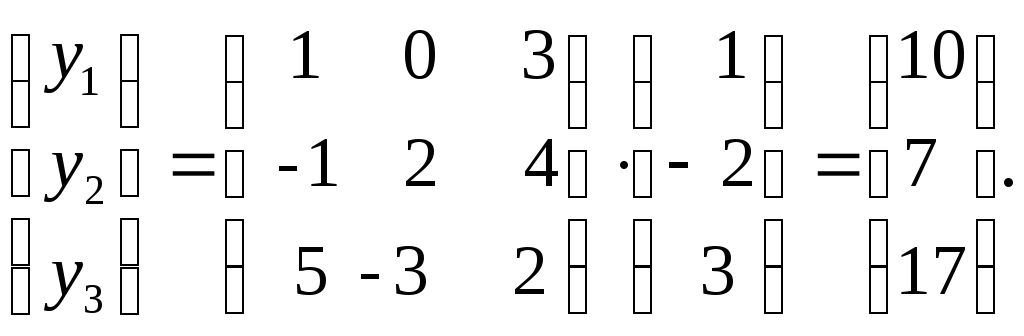
Ответ. y=10е₁ +7е₂ +17е_3.

2. Изменение матрицы линейного преобразования при переходе к новому базису

В параграфе 3.7. мы рассмотрели пересчет координат фиксированного вектора при переходе к новому базису, ввели понятие матрицы перехода. Теперь пусть в старом базисе е₁. е₂….,е_п имеется линейное преобразование в матричной форме

Q=AP, (4.2.1)

где Q – матрица-столбец, составленная из компонент вектора q=(q₁, q₂, …q_n) и P-матрица-столбец, составленная из компонент вектора р=(р₁,р₂….,р_т). А- матрица преобразования векторов

А=

При переходе к новому базису те же векторы р,q будут иметь новые координаты р= и . Преобразование имеет вид:

(4.2.2)

Найдем матрицу А´ из следующих соображений. По формуле (3.7.5) имеем:

Р=СР´ (4.2.3)

Q=CQ´ (4.2.4)

Здесь С - матрица перехода. В равенство (4.2.1) подставим (4.2.3) и (4.2.4), получим:

СQ´=ACP´ (4.2.5)

Умножим равенство (4.2.5) слева на матрицу С^-1, обратную матрице перехода: С^-1СQ´=С^-1АСР´.

Так как С^-1С=Е- единичная матрица, то получаем:

Q´=C^-1АСР´ (4.2.6)

Это и есть линейное преобразование векторов в новом базисе. Матрица линейного оператора в новом базисе вычисляется по формуле:

А´=С^-1АС (4.2.7)

Заметим, что из матричной формулы (4.2.7) следует числовое равенство Det(A´)=det(A), то есть величина определителя матрицы оператора не зависит от выбора базиса. Действительно, используя свойства определителей, получаем

.

Пример. В базисе е₁, е₂ преобразование имеет матрицу А=. Найти матрицу этого преобразования в новом базисе

Решение. Составим матрицу перехода к новому базису, располагая координаты векторов е₁´=(1,-1), е₂´=(3,2) по столбцам, С= . Вычислим обратную матрицу

С^-1=

Матрица оператора А в новом базисе будет получена по формуле (4.2.7):

Ответ. Матрица оператора в новом базисе равна .
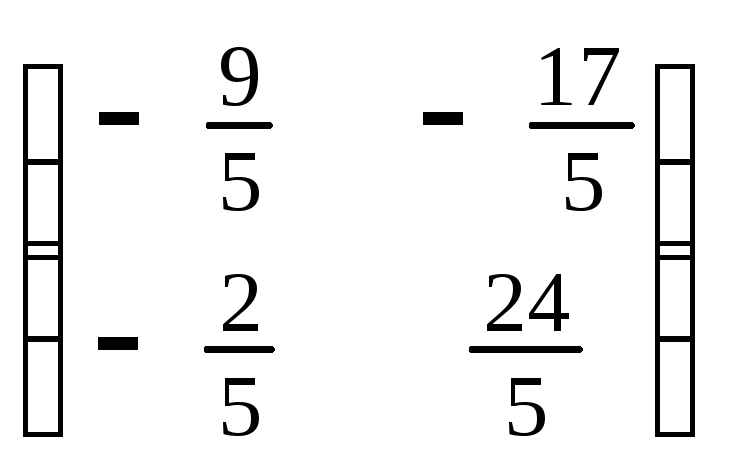