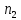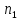2.7.1. Схема без возвращения с упорядочением

Из урны с n шарами извлекается m шаров по одному без возвращения, при этом порядок важен, т. е. какой шар окажется на первом, втором и т. д. местах имеет принципиальное значение. Первый шар может быть выбран n способами, второй n-1 способами (выбор из n-1 шара) и т. д. и, наконец, последний m-й шар - n-m+1 способами. Поскольку выбор шара на каждом шаге может комбинировать со всеми способами выбора остальных шаров, то общее количество возможных вариантов составляет

N=n(n-1)...[n-m+1] = = =.

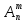Величина 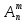, известная под названием “число размещений из n элементов по m ”, получена путем умножения и деления исходного выражения на одно и то же значение (n- m)!. Начальная часть формулы для случая m =n дает уже полученный ранее результат N=n!, а при m =0 из последней части формулы находим N=1, т.е. ни один элемент из любой совокупности может быть извлечен одним единственным способом, что совершенно очевидно. 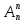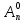Таким образом = n!, = 1.

	1 2 3 4 5 6
1 2 3 4 5 6	- 12 13 14 15 16 21 - 23 24 25 26 31 32 - 34 35 36 41 42 43 - 45 46 51 52 53 54 - 56 61 62 63 64 65 -

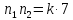Пример. Какова вероятность того, что последовательное расположение номеров двух шаров, наугад извлеченных без возвращения один за другим из урны с шестью перенумерованными шарами, даст двузначное число, кратное 7, т.е. делящееся на семь нацело. Таким образом, вводя соответствующие обозначения будем искать Р(“”), где - номера первого и второго шаров, а - натуральное число. В помощь решению задачи составим таблицу всех мыслимых исходов. Всего исходов N = 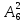= 6·5 = 30, что подтверждает таблица, при шести благоприятных исходах - по одному в каждой строке таблицы: 14, 21, 35, 42, 56, 63. Тогда искомая вероятность

Р(“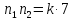”) = = 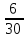= 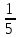20%,

что не так уж и мало.

2. 7.2. Схема без возвращения и без упорядочения

При извлечении из урны с n шарами m шаров одного за другим их порядок не имеет значения, т.е. выборки отличаются только составом. В этих условиях комбинации (1, 2) и (2, 1) в отличие от предыдущего примера становятся неразличимыми. Подобная ситуация может возникнуть, если на экзамене преподаватель по доброте душевной разрешает вытащить сразу два билета и тогда для студента по существу важна только его способность ответить на вопросы этих билетов и безразлично какая комбинация номеров ему досталась (3, 7) или (7, 3).

В совокупности из m шаров возможно произвести m! перестановок, которые по условию неразличимы между собой. Поэтому общее количество вариантов (исходов) по сравнению с предыдущей схемой должно быть меньше в m! раз и составит

N = = = .

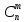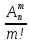Величина 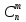называется числом сочетаний из n элементов по m.

Для обеспечения дееспособности данной формулы при всех целых 0£m£n чисто формально принимается 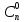= = 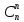1, поскольку не выбрать ни одного элемента (m=0) или выбрать все элементы из любой совокупности (m=n) в рассматриваемых условиях можно только одним способом.

Пример. В урне находится 7 черных шаров и 3 белых. Какова вероятность события А=”из 4-х наугад извлеченных шаров ровно 2 будут белыми”.

В силу отличия различных комбинаций из 4-х шаров исключительно одним составом всего исходов насчитывается

N = 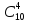= = 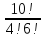= 210.

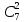Количество способов выбора двух белых и черных шаров равно соответственно = 3 и = 21. Поскольку каждый вариант выбора белых шаров может сочетаться с любым вариантом выбора черных шаров, то число благоприятных исходов выразится величиной 3·21=63 и, тогда,

Р(А) = 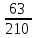= 0,3.