1. 2. Основные понятия и способы задания множеств

Множества будут обозначаться прописными, а их элементы строчными буквами. Принадлежность элемента 𝑚 множеству M записывается так: 𝑚M; а множества A множеству B: АВ или АВ

и при этом говорят, что множество А является подмножеством множества В. Использованный здесь знак строго включения “” означает, что 𝑎A ⇒ 𝑎B, но  𝑏B : 𝑏A, т.е. все элементы множества А являются одновременно элементами В, но при этом найдется такой элемент b множества B, который множеству А не принадлежит.

Важным свойством включения является транзитивность:

A  В и В  С ⇒ A  С;

⇒ А  С.

Пример: A  связка спелых бананов; B  множество всех бананов;

C  множество всех фруктов; D  множество всех продуктов питания. Тогда очевидно имеет место строгое включение ABCD, т.е. каждое предыдущее множество является подмножеством последующего множества.

Очевидно, что каждый элемент множества является его подмножеством: 𝑎A ⇒ {𝑎}  A.

Далее, АА (каждое множество является подмножеством самого себя). В последствие в процессе качественных рассуждений в случае A  В будет использовано выражение В “больше” А или А “меньше” В.

Множества А и В называются равными, если они состоят из одних и тех же элементов, т.е. элементы одного множества являются одновременно элементами другого множества или, что то же самое, каждое из этих множеств является подмножеством другого.

Иными словами равенство множеств означает совпадение их всех элементов в соответствии с принципом сравнения объектов путем их реального или мысленного наложения (сопоставления), который использует наш интеллект для этой цели.

В символьной записи это определение выглядит так:

А=В ⇔

Рассуждая от противного нетрудно убедиться, что АВ ⇔  𝑎A : 𝑎B или  bB : bA, а может и то и другое, т.е. в по крайней мере в одном из множеств найдется элемент, который другому множеству не принадлежит.

Простейшим способом задания конечного множества М из

𝑛 элементов является прямое перечисление его элементов в фигурных скобках с их нумерацией

М=.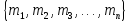

Пример: М={2, 0, -3}={0, -3, 2}. Перестановкой элементов множества подчеркивается произвольность порядка их перечисления.

Если множество М бесконечно, но, тем не менее, все его элементы можно перенумеровать, то такое множество называется счетным и оно может быть представлено в аналогичном виде

М=.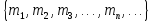

Помимо перечисления элементов множества можно описывать с помощью, так называемого характеристического свойства (признака), которое означает справедливость (истинность) некоторого утверждения только для элементов данного множества. Обозначим характеристическое свойство символом XS. Тогда множество М описывается как совокупность неких объектов, обладающих свойством XS:

М=.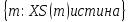

Возможна также запись

М=,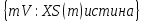

которая означает, что множество М состоит из тех элементов множества V, для которых утверждение .

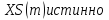Например, V=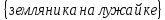, а ХS  “спелость”. Тогда

М  все спелые ягоды земляники на этой лужайке.

Математика имеет дело с множествами различной природы и, конечно же, с числовыми множествами, для которых приняты стандартные обозначения:

N  множество натуральных чисел (целых больших нуля);

Z  множество всех целых чисел (положительных и отрицательных);

Q  множество рациональных чисел (получаемых в результате

деления двух целых чисел);

R  множество вещественных или действительных чисел

(рациональных чисел в совокупности с иррациональными 

корнями из рациональных чисел).

Теперь, используя рассмотренные выше способы, нетрудно дать формализованное описание этих множеств:

N=;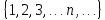

Z=;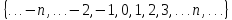

Q==;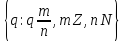

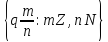R=.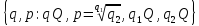

Множество вещественных положительных чисел как подмножество всех вещественных чисел может быть описано следующей фразой

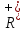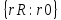
=  R,

где ”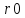”  характеристический признак.

Для двух множеств X и Y совокупность упорядоченных пар (𝑥, 𝑦), первый элемент которой принадлежит первому множеству, а второй  второму называется декартовым или прямым произведением указанных множеств и обозначается

X×Y= .

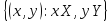В частности, декартово произведение самого на себя множества вещественных чисел как точек числовой оси дает геометрическую плоскость в виде множества точек в координатном представлении

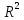=R×R=

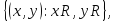
где линия 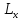= является осью абсцисс, а

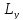=  осью ординат.

Примеры.

1. Пустое множество

V=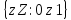= или U==.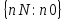

2. Множество целых чисел на интервале [0, 3)

C==.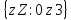

3. Интервал [-5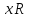, 3)={ : -5 𝑥3}.

4. Описать вторую четверть единичного круга (помечена штриховкой) как удовлетворяющее соответствующим условиям множество точек плоскости:

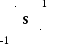
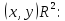
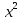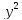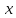S={ +≤1, [-1, 0],}.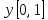

5. Прямоугольник 21 с правой нижней угловой точкой в начале координат может быть представлен в виде множества двояко  либо через характеристическое свойство, либо как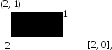

декартово произведение двух отрезков

Р={(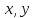): [2,0], [0,1] }=[2,0][0,1].

6. Прямое произведение двух конечных числовых множеств

А={1, 0, -3} и В={2, -3} дает 6 числовых пар

АВ={(1,2), (1,-3), (0,2), (0,-3), (-3,2), (-3,-3)}.

При этом

ВА≠ АВ.

{(2,1), (2,0), (2,-3), (-3,1), (-3,0), (-3,-3)} =

Неравенство в рамке означает, что декартово произведение не обладает свойством перестановочности множеств (коммутативность).