2.10. Формула полной вероятности
Пусть случайные
события
попарно
несовместны
и событие А
содержится
в их сумме А
Ì
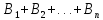, тогда справедлива формула полной
вероятности
Р(А)=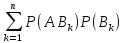
.
В данных условиях событие А можно представить в виде
А=А(
)
или А=
.
В
силу попарной несовместности событий
=∅
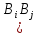при
≠
)
имеет место попарная несовместность
событий А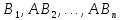
,
т.к.
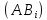(А
)=(А
)(
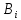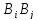А)=А
А=А(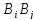
)А=А∅А=∅.
Далее, учитывая, что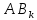 Р(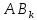
)=Р(
)Р(
)
окончательно находим
Р(А)=Р(
)=
.
События
интерпретируются
как условия наступления события А
и называются предпосылками события
А. События предпосылки принято называть
гипотезами.
Их вероятности известны до опыта и
потому называются априорными. Теперь
формулу полной вероятности можно
трактовать следующим образом:
вероятность
любого события разлагается в сумму
вероятностей
гипотез, взятых с коэффициентами
равными условным вероятностям данного
события относительно этих гипотез.
При
решении задач для обеспечения условий
применения формулы полной вероятности
предпосылки
выбирают
попарно несовместными и образующими
полный набор, т.е.
=Ω
.
Пример. В первой группе из 20 студентов 5 юношей, а во второй группе из 30 студентов - 3 юноши. Какова вероятность того, что выбранный наугад студент - юноша (событие А)?
Поскольку
выбранный студент числится в какой-либо
из двух групп, то в качестве гипотез
естественно принять его принадлежность
первой группе -
и
второй
группе -
.
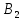Вероятности
гипотез найдем исходя из доли
численности групп в общем количестве
студентов:
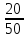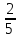Р(
)=
=
, Р(
)=
=
.
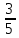Затем найдем соответствующие условные вероятности, исходя, на сей раз из доли юношей в каждой группе
=
=
,
=
=
.
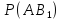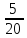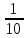И, наконец, вычислим окончательный результат
Р(А)=
·
+
·
=
=
.
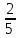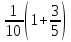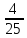Простота задачи позволяет проконтролировать полученное решение с помощью классической схемы. Поскольку выбор производится из совокупности в количестве 50 студентов при наличии в ней 8 юношей, то в соответствии с формулой классической вероятности
Р(А)
=
=
,
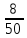чего и следовало ожидать.
При расчете вероятности сложных событий с использованием формулы полной вероятности схему решения задачи удобно иллюстрировать, систематизировать и анализировать с помощью, так называемого дерева вероятностей, ветви которого описывают все мыслимые сценарии развития каждой возможной начальной ситуации. Для рассмотренной задачи дерево вероятностей будет иметь структуру, изображенную ниже.
