2. 8. Геометрическая вероятность

Одним из классических экспериментов теории вероятностей является “вбрасывание точки” в некоторую геометрическую замкнутую область. Для определенности зададим на плоскости квадрат со стороной равной 1 и обозначим его Ω. В этот квадрат наугад вбрасывается точка и гарантированно в него попадает. Более того, предполагается, что все точки квадрата равноправны и потому все исходы такого эксперимента равновозможны в смысле попадания в любую точку Ω. Эксперимент имеет бесконечное множество равновозможных и несовместных исходов, каждый из которых отождествляется с точкой квадрата с координатами (𝑥, 𝑦). Обозначим А некоторую подобласть Ω, как это показано на рисунке, и будем считать событием А попадание в одноименную область. Прозвучавшие выше термины равновозможности, несовместности и благоприятности свидетельствуют, что мы уже совсем близки к применению формулы классической вероятности. Осталось только конкретизировать способ численного определения количества благоприятных исходов и всех мыслимых исходов. Поскольку в качестве интегральных числовых характеристик этих исходов реально мы располагаем только размерами одноименных площадей, то количество исходов каждого вида отождествляется с соответствующими площадями. При этом площадь квадрата S(Ω) выражает общее количество исходов, а S(А) - число благоприятных исходов. Тогда в соответствии с определением классической вероятности как отношения числа благоприятных исходов к общему количеству равновозможных и несовместных исходов для расчета так называемой геометрической вероятности события А получаем формулу

Р(А) =.

Применительно к ситуации, изображенной на рисунке, находим

Р(А) = = 0,35.

Геометрическая вероятность обладает всеми свойствами классической вероятности:

- отношение площади вложенной фигуры А к площади Ω неотри-

цательно и не превосходит 1;

- несовместным событиям отвечают непересекающиеся области и

потому их сумме соответствует суммарная площадь;

- полному набору событий соответствует разбиение Ω на непересе-

кающиеся области, дающие в своем объединении Ω.

Для иллюстрации практического применения геометрической вероятности рассмотрим следующую задачу: юноша и девушка договорились о встрече между 19 и 20 часами, поклялись непременно придти и условились, что один ждет другого только 15 мин, а затем уходит. Какова вероятность их встречи.

Преодолев первоначальное замешательство от такой постановки вопроса, напряжем свои логические способности. Очевидно, что сначала надо выжать все возможное из имеющихся исходных данных и затем распорядиться полученной информацией сообразно ее содержанию. Итак, интервал встречи составляет 1 час. Поскольку влюбленные гарантированно приходят в этот интервал времени, то разумно обозначить время их прихода в долях часа: 𝑥 - пришел юноша; 𝑦 - пришла девушка. Тогда 0 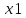, . По условию задачи для встречи необходимо, чтобы разность между моментами их прихода вне зависимости от того кто пришел первым не превышала часа, т.е. . При наличии двух параметров 𝑥 и 𝑦 в голову сразу же приходит мысль о декартовой системе координат, в которой моменты прихода изобразятся на плоскости точкой (𝑥 , 𝑦) с соответствующими координатами. Причем все точки улягутся точно в квадрат с единичной стороной. Например, если юноша и девушка пришли в 19.30 и 19.40, то такая ситуация отождествится с точкой квадрата (, 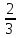). Далее, займемся препарированием модульного неравенства и с помощью школьных знаний без большого труда получим два неравенства:

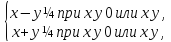
которые в своей совокупности устанавливают ограничения на возможные изменения параметра 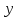: Обратившись к разделу “Линейное программирование” п. 5.6 нетрудно установить, что это двойное неравенство задает на плоскости область между двумя прямыми : , и : -, ограниченную

еще к тому же рамками квадрата Ω. В самом деле, построив эти прямые по двум точкам их пересечения со сторонами Ω

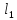{: (, 0), (1, )}, { : (0, ), ( , 1) }, и определив с помощью их нормальных векторов =(1, -1) и =( -1, 1) зоны действия соответствующих неравенств получим фигуру В, обозначенную на рисунке штриховкой. Каждая точка В гарантирует встречу молодых людей,

т.е. является благоприятной для одноименного события В=”встреча состоялась”. Теперь для решения задачи с полным основанием можно применить формулу геометрической вероятности. Площадь фигуры В удобно вычислить как разность площади Ω и общей площади двух не заштрихованных треугольников, которые будучи сложенными вместе по гипотенузе дадут квадрат со стороной . Тогда

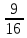Р(В) == = 1- = < = 50%.

Полученный результат свидетельствует, что при заданных исходных данных вероятность встречи молодых людей несколько меньше 0.5, т.е. встреча скорее не произойдет, нежели состоится.

Таким образом, задача о встрече успешно решена с помощью изначально не очевидных, но простых геометрических построений. Рассмотренный пример изящного применения аппарата ТВ вкупе с приведенными выше схемами выбора шаров из урны демонстрируют широту и мощь прикладных возможностей этой науки.

Ранее говорилось, что вероятность суммы двух несовместных случайных событий равна сумме их вероятностей. Геометрическая вероятность помогает установить правило вычисления вероятности суммы двух событий в случае их совместности. Для начала вспомним иллюстрацию этой ситуации кругами Эйлера в случае совместности случайных событий. Здесь АВ - произведение соответствующих событий. Очевидно, что S(А+В) = S(А)+S(В)-S(АВ),

поскольку при сложении площадей А и В площадь их пересечения АВ будет учтена дважды - в составе А и В. Поэтому следуя принципам геометрической вероятности в случае совместности случайных событий получаем

Р(А+В)=Р(А)+Р(В)-Р(АВ)

и если события несовместны, то в силу Р(АВ)=0 данная формула превращается в полученное ранее правило - “вероятность суммы двух несовместных случайных событий равна сумме их вероятностей”. В противном случае в этой формуле появляется поправочный член, учитывающий совместность случайных событий в виде вероятности их произведения. Хотя данная формула верна в общем случае приведенные здесь рассуждения не являются строгим доказательством и скорее могут рассматриваться в качестве мнемонического правила.