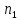2. 7.3. Схема с возвращением и с упорядочением

Из урны с n шарами m раз повторяется процедура извлечения шара и его возвращения обратно с фиксацией порядка вытащенных шаров. На каждом шаге такого эксперимента ситуация одна и та же - выбирается любой из n шаров, что естественно может быть сделано n способами. В результате опыта образуется набор из m шаров, в котором каждый шар может комбинировать с каждым, в том числе и с самим собой. Всего возможных исходов

N = n· n· . . . · n = .

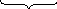
m

Пример. Из телефонной книги с 7-значными номерами наугад выбирается номер. Найти вероятность того, что все цифры в номере различны, если все комбинации цифр в номере равновозможны. Иными словами условиями задачи с целью упрощения допускаются номера 0000000, 0001111, 1010101 и т.п.

Общее количество номеров в такой схеме N = = 10000000.

Благоприятные исходы представляют наборы из 7 цифр, отличающиеся не только самими цифрами, но и их порядком. Тогда количество благоприятных исходов определяется числом размещений m = и потому

Р(А) = ≈ 0,06=6%.

2.7.4. Схема с возвращением без упорядочения

Из урны с n шарами m раз извлекается шар и возвращается обратно без учета порядка. В результате эксперимента образуются комбинации из m шаров, отличающиеся только своим составом. Такой опыт эквивалентен извлечению одновременно m шаров из урны с n +m -1 шарами c подсчетом общего числа исходов с помощью числа сочетаний. Здесь “-1” образуется вследствие того, что возвращение последнего шара в урну уже никак не может повлиять на результат. Убедиться в этом помогает пример выбора одного единственного шара, что может быть сделано n способами. При этом 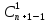= = = 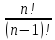n, как тому и следует быть.

Пример. Покупатель в кондитерской выбил чек на 4 пирожных из 7 видов, имеющихся в продаже. Какова вероятность того, что куплены пирожные: одного вида (событие А); разных видов (В); две пары разных видов (С). Содержание данной задачи соответствует схеме выбора с возвращением без упорядочения. В самом деле, купив один эклер можно купить и второй (возвращение) и при этом, какой из них куплен первым не имеет ровным счетом никакого значения.

Общее количество исходов составляет N== =210.

Число благоприятных исходов для события А определяется исходя из общего количества разных видов пирожных m(А)=7 и потому

Р(А) = = .

Во втором случае благоприятными являются наборы из 4-х различных пирожных, отличающиеся только составом, т.е. m(В)=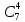=35 и, следовательно,

Р(В) = = .

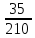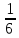Поскольку из 7 элементов можно сгруппировать =21 различную пару, то событие С реализуется с вероятностью

Р(С) = = .

	1 2 3 4 5 6 7
1 2 3 4 5 6 7	- 12 13 14 15 16 17 - - 23 24 25 26 27 - - - 34 35 36 37 - - - - 45 46 47 - - - - - 56 57 - - - - - - 67 - - - - - - -

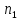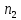Для того, чтобы убедиться в правильности подсчета количества благоприятных исходов достаточно составить таблицу с их перечислением, предварительно перенумеровав все 7 видов пирожных и обозначив символами и номера первой и второй пары. Полученный результат свидетельствует, что наиболее вероятным является событие В.