Поле движущегося заряда. Закон Био-Савара.
Магнитное поле движущегося заряда.
Покоящийся заряд
![]() создает в окружающем пространстве
только электрическое поле. Это поле
изотропно, и центр симметрии
электростатического поля определяется
только положением заряда.
создает в окружающем пространстве
только электрическое поле. Это поле
изотропно, и центр симметрии
электростатического поля определяется
только положением заряда.
Если заряд
![]() движется со скоростью
движется со скоростью
![]() ,
то в пространстве появляется выделенное
направление, связанное с направлением
этого движения. Поэтому создаваемое
движущимся зарядом
,
то в пространстве появляется выделенное
направление, связанное с направлением
этого движения. Поэтому создаваемое
движущимся зарядом
![]() магнитное поле имеет осевую симметрию.
магнитное поле имеет осевую симметрию.
В результате обобщения экспериментальных данных был получен элементарный закон, получивший название закона Био-Савара:
точечный заряд
![]() ,
равномерно движущийся с малой
(нерелятивистской,
,
равномерно движущийся с малой
(нерелятивистской,
![]() )
скоростью, создает в окружающем
пространстве магнитное поле:
)
скоростью, создает в окружающем
пространстве магнитное поле:
|
|
|
где
![]() - радиус-вектор, проведенный от заряда
- радиус-вектор, проведенный от заряда
![]() к точке наблюдения,
к точке наблюдения,
![]() - магнитная постоянная
(с системе СИ
- магнитная постоянная
(с системе СИ
![]() Гн/м).
Гн/м).
|
|
Конец радиус-вектора
|
|
|
В соответствии с приведенной формулой
вектор
![]() направлен перпендикулярно плоскости,
в которой расположены векторы
направлен перпендикулярно плоскости,
в которой расположены векторы
![]() и
и
![]() ,
причем вращение вокруг вектора
,
причем вращение вокруг вектора
![]() в направлении вектора
в направлении вектора
![]() образует с направлением
образует с направлением
![]() правовинтовую систему.
правовинтовую систему.
Магнитное поле тока.
|
|
Найдем магнитное поле, создаваемое
элементом тока
|
|
|
где
![]() - скорость хаотического движения, а
- скорость хаотического движения, а
![]() - скорость направленного движения
(дрейфа) носителей. Вычисляя магнитное
поле элемента тока, мы будем исходить
из установленного опытным путем принципа
суперпозиции. Следуя этому принципу,
мы будем считать, что каждый заряд
- скорость направленного движения
(дрейфа) носителей. Вычисляя магнитное
поле элемента тока, мы будем исходить
из установленного опытным путем принципа
суперпозиции. Следуя этому принципу,
мы будем считать, что каждый заряд
![]() возбуждает поле, совершенно не зависящее
от наличия других зарядов.
возбуждает поле, совершенно не зависящее
от наличия других зарядов.
Число носителей, содержащихся в этом
элементе с поперечным сечением
![]() :
:
|
|
|
Усредняя по всем носителям, заключенным
в объеме
![]() ,
получаем
,
получаем
|
|
|
и, умножая на количество носителей,
заключенных в объеме
![]() ,
находим
,
находим
|
|
|
Или окончательно
|
|
|
Итак, закон Био-Савара: магнитное поле от объемного элемента тока:
|
|
|
магнитное поле от линейного элемента тока:
|
|
|
Примеры расчета магнитных полей.
-
Вычислим магнитное поле прямого тока, т.е. тока, текущего по тонкому прямому бесконечно длинному проводу.
|
|
Согласно закону Био-Савара в некоторой
произвольно выбранной точке
|
|
|
Из рисунка следует, что
![]() и
и
![]() .
Поэтому
.
Поэтому
|
|
|
Интегрируя последнее выражение по всем
элементам тока, что эквивалентно
интегрированию по углу
![]() в пределах от
в пределах от
![]() до
до
![]() ,
находим
,
находим
|
|
|
-
Сила взаимодействия 2-х параллельных токов.
Индукция поля, создаваемого прямым
током
![]() ,
равна
,
равна
![]() .
Тогда сила, действующая на элемент
.
Тогда сила, действующая на элемент
![]() прямого
тока
прямого
тока
![]() со стороны тока
со стороны тока
![]() ,
,
|
|
|
а сила взаимодействия (притяжения) на единицу длины проводника:
|
|
|
|
|
-
Магнитное поле на оси кругового тока.
|
|
Выделим в правой части витка элемент
тока
Очевидно, что результирующий вектор
индукции магнитного поля
Чтобы найти модуль вектора
|
|
|
Проекция на ось
![]() вектора
вектора
![]() от любого элемента кругового тока равна
от любого элемента кругового тока равна
|
|
|
где учтено, что угол между элементом
![]() и радиус-вектором
и радиус-вектором
![]() равен
равен
![]() .
.
Интегрируя это выражение по
![]() (это дает
(это дает
![]() )
и учитывая, что
)
и учитывая, что
|
|
|
получаем, что поле на оси витка на
расстоянии
![]() от его центра:
от его центра:
|
|
|
В центре витка:
|
|
|
О системах единиц.
Закон взаимодействия токов послужил основой для определения электромагнитных единиц.
1) Посмотрим как строится система СГСЭ
(CGSE).
Основными в этой системе единиц являются:
см, грамм,
секунда и
единица заряда
CGSE
из закона Кулона
![]() .
Следовательно, магнитные величины уже
не произвольны. Так, сила, действующая
на 1 длины провода
.
Следовательно, магнитные величины уже
не произвольны. Так, сила, действующая
на 1 длины провода
![]() ,
и константа
,
и константа
![]() размерны.
размерны.
Опыты показали, что
![]() ,
где
,
где
![]() электродинамическая
постоянная, которая равна скорости
света в вакууме с
31010
см/с (Максвелл показал, что свет это
э/м волна).
электродинамическая
постоянная, которая равна скорости
света в вакууме с
31010
см/с (Максвелл показал, что свет это
э/м волна).
-
Система СГСМ (CGSM) строится также как СГСЕ - основные механические единицы те же: см, г, с, но дальше используют закон взаимодействия токов
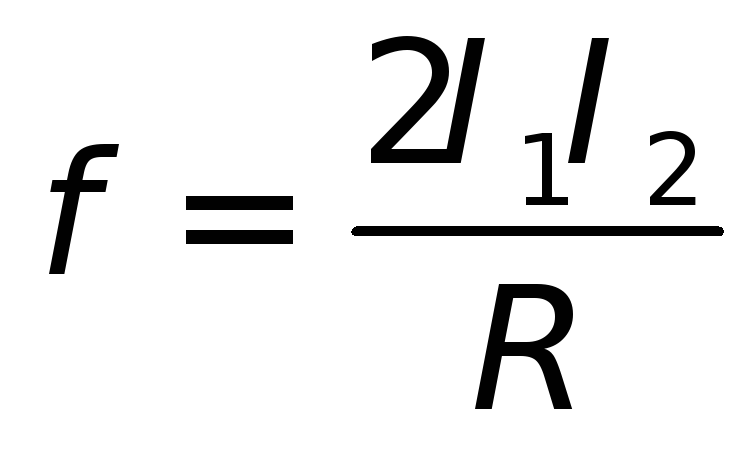 (здесь k=1)
для определения единицы силы тока. 1
CGSMтока
равна такому току, который, протекая
по бесконечному тонкому проводу,
действует на параллельный такой же
ток, находящийся на расстоянии в 1
см, с силой в 2
Дн. Тогда в системе имеем законы
Ампера и Био-Савара без дополнительных
коэффициентов:
(здесь k=1)
для определения единицы силы тока. 1
CGSMтока
равна такому току, который, протекая
по бесконечному тонкому проводу,
действует на параллельный такой же
ток, находящийся на расстоянии в 1
см, с силой в 2
Дн. Тогда в системе имеем законы
Ампера и Био-Савара без дополнительных
коэффициентов: -
Система СИ - основные единицы: м, кг, с и сила тока измеряется в А (Амперах). Основа определения силы тока является уравнение:
|
|
|
1 Ампер - это ток, который, проходя по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии в 1м в вакууме, вызвал бы силу на 1м каждого проводника, равную 210-7 Н.
Поток и циркуляция вектора магнитной индукции.
Как и любое векторное поле, магнитное
поле может быть наглядно представлено
с помощью линий вектора магнитной
индукции
![]() .
Их проводят обычным способом – так,
чтобы касательные к этим линиям в каждой
точке совпадали с направлением вектора
.
Их проводят обычным способом – так,
чтобы касательные к этим линиям в каждой
точке совпадали с направлением вектора
![]() ,
а густота линий была бы пропорциональна
модулю вектора
,
а густота линий была бы пропорциональна
модулю вектора
![]() в данном месте. Геометрическая картина
позволяет судить о конфигурации
конкретного магнитного поля и значительно
облегчает анализ некоторых ситуаций.
в данном месте. Геометрическая картина
позволяет судить о конфигурации
конкретного магнитного поля и значительно
облегчает анализ некоторых ситуаций.
Теорема Гаусса для поля вектора
![]() .
Поток вектора магнитной
индукции
.
Поток вектора магнитной
индукции
![]() сквозь любую замкнутую поверхность
равен нулю.
сквозь любую замкнутую поверхность
равен нулю.
|
|
|
Эта теорема является, по существу, обобщением опыта.
|
Она выражает в постулативной
форме тот экспериментальный факт, что
линии вектора
Поток вектора
Рассматриваемая теорема
выражает и тот факт, что в
природе нет магнитных зарядов,
на которых начинались или заканчивались
бы линии вектора
|
Стягивая объем, заключенный внутри
поверхности
![]() к интересующей нас точке поля, или
воспользовавшись т. Гаусса-Остроградского
к интересующей нас точке поля, или
воспользовавшись т. Гаусса-Остроградского
![]() ,
можем записать т. Гаусса
для вектора
,
можем записать т. Гаусса
для вектора
![]() в дифференциальной форме:
в дифференциальной форме:
|
|
|
Полученное выражение имеет фундаментальный характер: оно справедливо не только для постоянных, но и для переменных магнитных полей.
|
25 |
Магнитный момент. Закон полного тока. Контур с током в магнитном поле. Работа по перемещению контура с током в магнитном поле. Сила Лоренца. Эффект Холла. Применение МГД явлений в науке и технике. |
Теорема о циркуляции вектора
![]() (для магнитного поля постоянных токов).
(для магнитного поля постоянных токов).
Циркуляция вектора
магнитной индукции
![]() поля постоянных токов по произвольному
замкнутому контуру равна произведению
поля постоянных токов по произвольному
замкнутому контуру равна произведению
![]() на алгебраическую сумму токов,
пронизывающих контур циркуляции.
на алгебраическую сумму токов,
пронизывающих контур циркуляции.
|
|
|
|
|
Докажем эту теорему для прямого тока
![]() и
контура
и
контура
![]() ,
лежащего в плоскости, перпендикулярной
направлению тока.
,
лежащего в плоскости, перпендикулярной
направлению тока.
|
|
|
Согласно закону Био-Савара в каждой
точке контура
![]() вектор
вектор
![]() поля прямого тока
поля прямого тока
![]() направлен по касательной к окружности,
проходящей через эту точку, а модуль
вектора индукции магнитного поля равен
направлен по касательной к окружности,
проходящей через эту точку, а модуль
вектора индукции магнитного поля равен
|
|
|
где
![]() - расстояние от оси тока до интересующей
нас точки.
- расстояние от оси тока до интересующей
нас точки.
|
|
|
где
![]() - проекция вектора
- проекция вектора
![]() на направление вектора
на направление вектора
![]() .
.
(Здесь
![]() элемент контура циркуляции. Не путать
с элементом проводника с током!)
элемент контура циркуляции. Не путать
с элементом проводника с током!)
Тогда
|
|
|
|
|
|
Если контур
|
|
|
|
||
Этот результат легко обобщить на
произвольно ориентированный относительно
направления тока контур. При этом под
![]() следует понимать проекцию угла, под
которым виден элемент контура
следует понимать проекцию угла, под
которым виден элемент контура
![]() ,
на плоскость, перпендикулярную направлению
тока. Чтобы обобщить полученный результат
на случай произвольных токов достаточно
воспользоваться принципом суперпозиции
для вектора
,
на плоскость, перпендикулярную направлению
тока. Чтобы обобщить полученный результат
на случай произвольных токов достаточно
воспользоваться принципом суперпозиции
для вектора
![]() .
.
|
Итак, равенство
справедливо для любых токов и произвольно ориентированных контуров.
|
Если токи распределены непрерывно, то
![]() ,
где
,
где
![]() - площадь поверхности, опирающейся на
контур
- площадь поверхности, опирающейся на
контур
![]() .
В этом случае теорема о циркуляции
принимает вид:
.
В этом случае теорема о циркуляции
принимает вид:
|
|
|
Иногда теорему о циркуляции
вектора
![]() называют законом
полного тока.
называют законом
полного тока.
Тот факт, что циркуляция
вектора
![]() ,
вообще говоря, не равна нулю, означает,
что магнитное поле не потенциально (в
отличие от электростатического). Такое
поле называют вихревым
или соленоидальным.
,
вообще говоря, не равна нулю, означает,
что магнитное поле не потенциально (в
отличие от электростатического). Такое
поле называют вихревым
или соленоидальным.
Дифференциальная форма теоремы о
циркуляции вектора
![]() .
.
К дифференциальной форме теоремы о циркуляции можно также перейти, воспользовавшись т. Стокса.
|
|
|
От интеграла, выражающего циркуляцию
вектора
![]() по замкнутому контуру
по замкнутому контуру
![]() ,
переходим к интегралу по поверхности
,
переходим к интегралу по поверхности
![]() ,
определяющему поток вектора
,
определяющему поток вектора
![]() .
Тогда
.
Тогда
|
|
|
и в силу произвольности выбора контура
(поверхности
![]() )
получаем
)
получаем
|
|
|
Символом
![]() обозначен вектор
обозначен вектор
|
|
|
Формально
![]() можно рассматривать как векторное
произведение дифференциального оператора
можно рассматривать как векторное
произведение дифференциального оператора
|
|
|
на вектор
![]() ,
т.е.
,
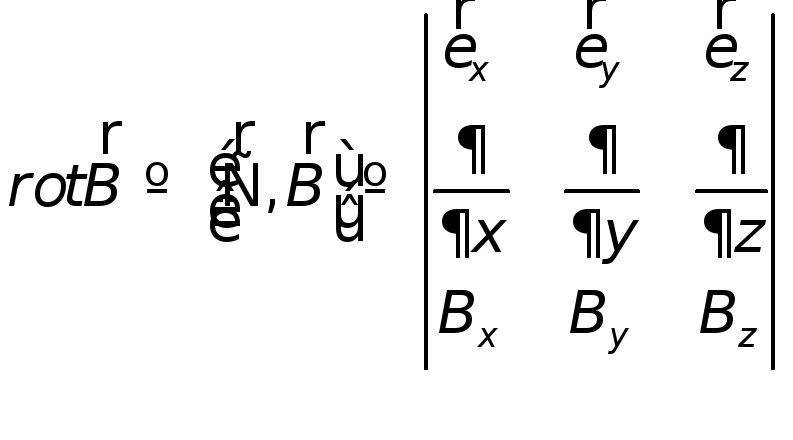
т.е.![]()
|
|
|
Примеры вычисления магнитных полей.
-
Пустотелый проводящий цилиндр радиусом
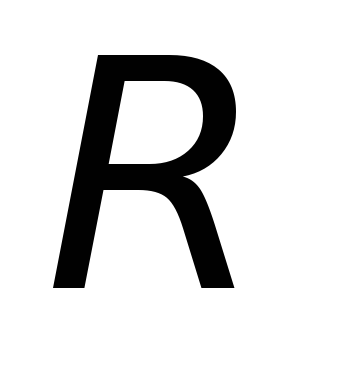 .
.
А. Поле внутри цилиндра.
Поскольку внутри цилиндра токов нет, то
 и
и
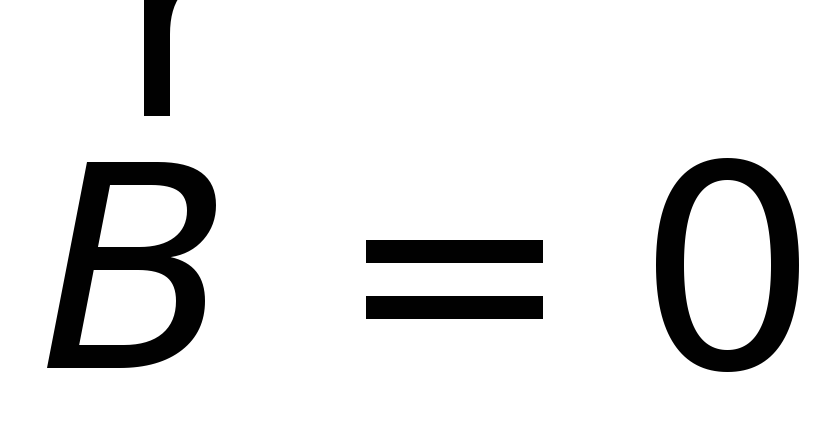 .
.Б. Поле снаружи.
По теореме о циркуляции:
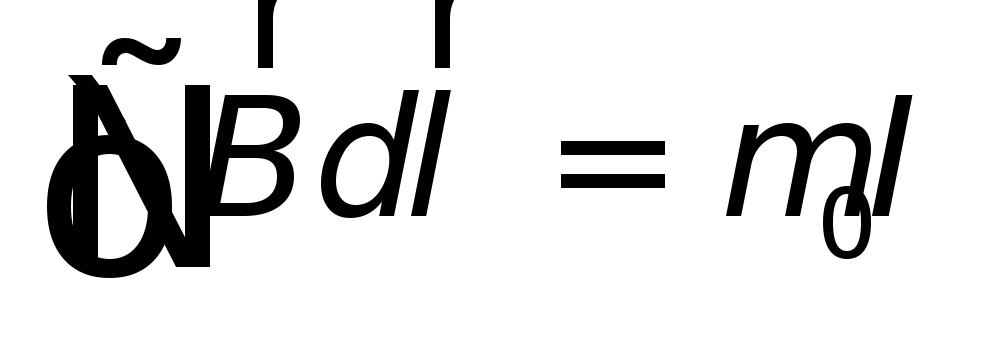 ,
откуда
,
откуда
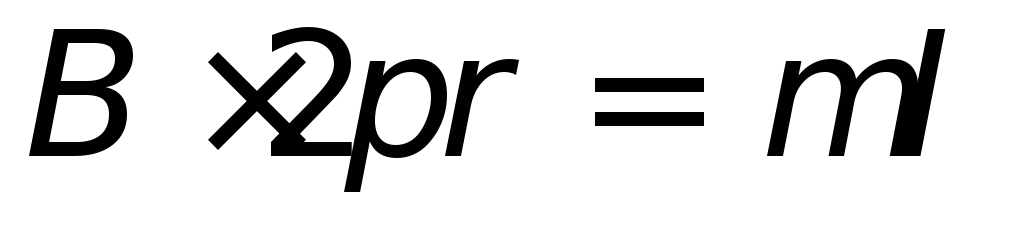 и
и
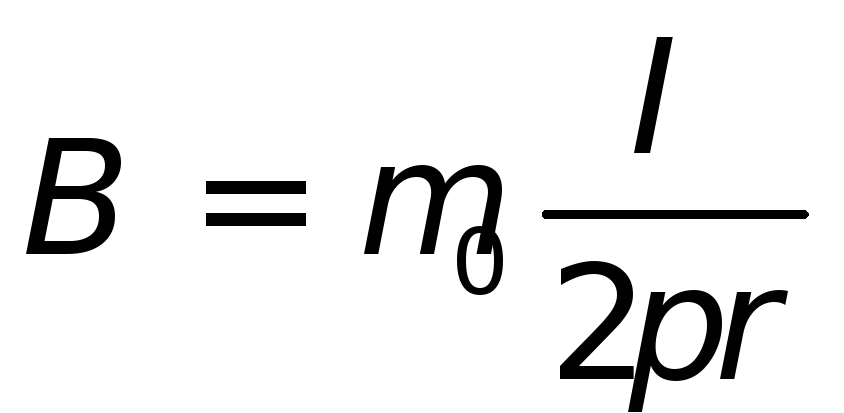
-
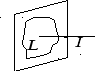
Поле внутри длинного соленоида:
|
|
Выберем контур, проходящий внутри
соленоида и снаружи, как показано на
рисунке. Легко увидеть из симметрии,
что поле внутри направлено вдоль оси
соленоида, поэтому циркуляция вектора
|
|
|
контура равна нулю
|
|
|
Вне длинного соленоида поле также равно нулю (можно уйти на бесконечность, где поле всегда равно нулю), поэтому циркуляция индукции магнитного поля по выбранному контуру равна:
|
|
|
где
![]() плотность
витков (количество витков на единицу
длины),
плотность
витков (количество витков на единицу
длины),
![]() ток
через соленоид.
ток
через соленоид.
Итак, поле внутри соленоида равно:
|
|
|
Магнитный момент и магнитное поле витка с током.
Магнитный момент витка с током:
|
|
|
Выражение, описывающее магнитное поле
![]() ,
созданное витком с током, по форме в
точности совпадает с выражением для
напряженности электрического поля
,
созданное витком с током, по форме в
точности совпадает с выражением для
напряженности электрического поля
![]() электрического диполя:
электрического диполя:
|
|
|



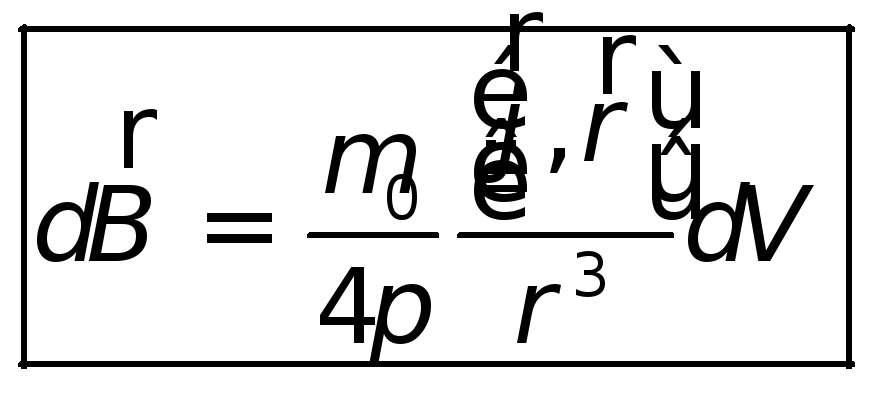 ,
,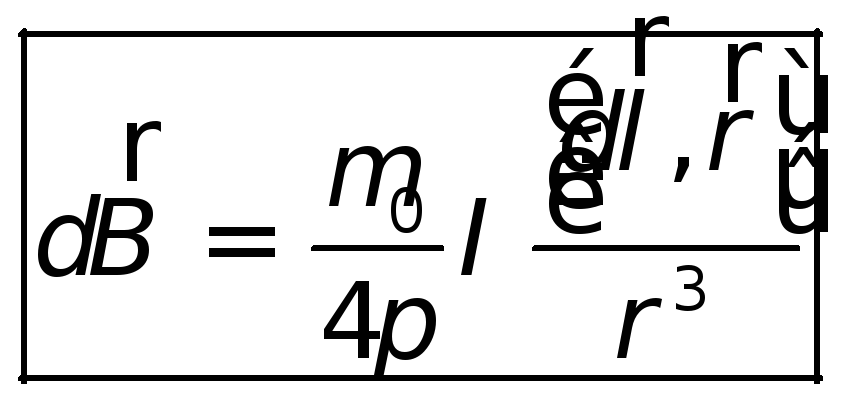 .
.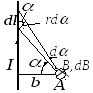
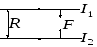
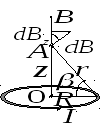
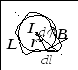
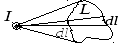
 .
.