59.Метод зведення визначника до трикутного вигляду Визначником трикутного вигляду відносно головної діагоналі називається визначник, всі елементи якого, що стоять вище або нижче головної діагоналі, дорівнюють нулю. Такий визначник дорівнює добутку елементів його головної діагоналі. = a11a22…ann , де n – порядок визначника. a1na2,n-1…an1 Метод зведення визначника до трикутного вигляду полягає в тому, що, користуючись властивостями визначників, даний визначник перетворюється так, щоб одержати визначник трикутного вигляду відносно головної або побічної діагоналі, і далі одержується результат. Нехай задано визначник n–го порядку загального вигляду. Згідно з властивостями визначників, ці перетворення не змінюють величини визначника (. Одержуємо визначник . Всі ці перетворення не змінюють величини визначника. В результаті одержуємо визначник . Продовжуючи цей процес одержання нулів нижче головної діагоналі, через скінчене число кроків або переконаємось в тому, що ( = 0, або зведемо визначник до трикутного вигляду відносно головної діагоналі. В цьому випадку , причому x11= a11( 0, x22= b22( 0, x33= c33 ( 0,…, xnn ( 0. Отже, ( = x11x22x33...xnn Методом зведення до трикутного вигляду можна обчислювати визначники малих порядків. Приклад 1. Обчислити визначник Розв’язування. Перший стовпчик визначника ненульовий, і в ньому на першому місці стоїть ненульовий елемент. Тому можна в першому стовпчику одержати нулі на всіх місцях, починаючи з другого. Для цього від другого рядка віднімаємо перший, помножений на 2: . Далі від третього рядка віднімаємо перший, помножений на 3: . Від четвертого рядка віднімаємо перший, помножений на 2: . Нарешті від п’ятого рядка віднімемо перший: . У другому стовпчику одержаного визначника на другом місці знаходиться ненульовий елемент. Тому одержуємо нулі у другому стовпчику на всіх місцях, починаючи з третього. Для цього від третього рядка віднімемо другий, від четвертого віднімемо другий, помножений на 11, і до п’ятого рядка додамо другий, помножений на 2. У третьому стовпчику одержаного визначника на другому місці знаходиться ненульовий елемент. Одержуємо нулі у третьому стовпчику, починаючи з четвертого місця. Для цього до четвертого рядка додамо третій помножений на 10, а від п’ятого віднімемо третій, помножений на 4 . і одержати визначник трикутного вигляду відносно головної діагоналі . = 52 На практиці рекомендується при обчисленні визначників з цілими елементами на кожному кроці одержувати визначники також з цілими елементами. У нашому випадку перед виконанням останнього кроку перетворень можна було, наприклад, перейти від визначника до визначника відніманням від п’ятого рядка четвертого, помноженого на 2. Далі переставимо четвертий і п’ятий рядки. Як відомо, при цьому змінюється знак визначника: . Нарешті до п’ятого рядка додамо четвертий, помножений на 3: . Таким чином, ( = - (1((-1)(1(1( 52) = 52. Розглянемо тепер деякі приклади обчислення визначників n–го порядку методом зведення до трикутного вигляду. При обчисленні визначників n–го порядку будемо суттєво користуватись закономірностями в будові цих визначників.

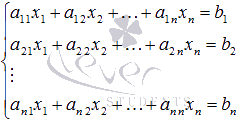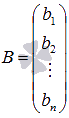65. , которые в матричной форме записываются как , где - основная матрица системы, - матрица-столбец неизвестных переменных, - матрица свободных членов. Сначала опишем суть матричного метода, остановимся на условии применимости этого метода, далее подробно разберем решения нескольких примеров. Сразу оговоримся, что решение систем линейных алгебраических уравнений матричным методом и решение СЛАУ с помощью обратной матрицы есть одно и то же. Поэтому рекомендуем освежить в памяти теорию раздела обратная матрица: определение, свойства, методы нахождения. Приступим. Пусть для матрицы А порядка n на n существует обратная матрица . Умножим обе части матричного уравнения слева на (порядки матриц A ⋅ X и В позволяют произвести такую операцию, смотрите статью операции над матрицами, свойства операций). Имеем . Так как для операции умножения матриц подходящих порядков характерно свойство ассоциативности, то последнее равенство можно переписать как , а по определению обратной матрицы (E – единичная матрица порядка n на n), поэтому 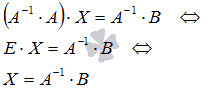Таким образом, решение системы линейных алгебраических уравнений по матричному методу определяется равенством . Другими словами, решение СЛАУ находится с помощью обратной матрицы . Мы знаем, что квадратная матрица А порядка n на n имеет обратную матрицу только тогда, когда ее определитель не равен нулю. Следовательно, СИСТЕМУ n ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ. Рассмотрим матричный метод на примерах. В некоторых примерах мы не будем подробно описывать процесс вычисления определителей матриц, при необходимости обращайтесь к статье вычисление определителя матрицы. Пример. С помощью обратной матрицы найдите решение системы линейных уравнений 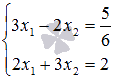. Решение. В матричной форме исходная система запишется как , где 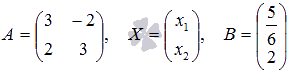. Вычислим определитель основной матрицы и убедимся, что он отличен от нуля. В противном случае мы не сможем решить систему матричным методом. Имеем 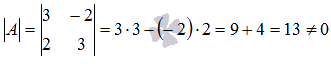, следовательно, для матрицы А может быть найдена обратная матрица . Таким образом, если мы отыщем обратную матрицу, то искомое решение СЛАУ определим как . Итак, задача свелась к построению обратной матрицы . Найдем ее. Мы знаем, что для матрицы 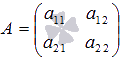обратная матрица может быть найдена как 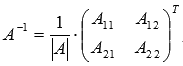, где - алгебраические дополнения элементов . В нашем случае 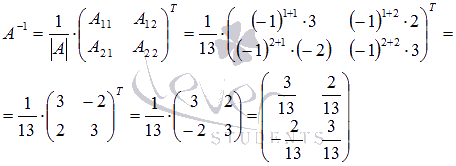Тогда 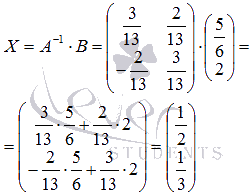Выполним проверку полученного решения 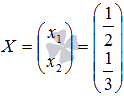, подставив его в матричную форму исходной системы уравнений . Это равенство должно обратиться в тождество, в противном случае где-то была допущена ошибка.

Следовательно, решение найдено верно. Ответ: или в другой записи .

69.

Скалярний добуток двох векторів

Def.   Скалярним добутком двох векторів  і  називають число  (або ), що дорівнює добутку довжин цих векторів на косинус кута між ними.

.

Якщо хоча б один із векторів  чи  нульовий, то за означенням

.

Оскільки виконуються рівності

,     ,

то

.

Геометричний зміст скалярного добутку.

Рис. 14. Геометричний зміст скалярного добутку

Скалярний добуток двох векторів дорівнює добутку довжини одного вектора на проекцію на нього другого вектора (рис. 14). Тоді .          (5.1)

 Формула (5.1) – робоча формула для обчислення проекції вектора на вектор (або вісь).

Властивості скалярного добутку

Алгебраїчні властивості скалярного добутку :

1) ; 

2) ;

3) .

Геометричні властивості скалярного добутку:

1) якщо  та , то , якщо кут  гострий, і , якщо кут  тупий;

2) скалярний добуток двох ненульових векторів дорівнює нулю тоді і тільки тоді, коли ці вектори перпендикулярні;

3) скалярний квадрат вектора дорівнює квадрату його довжини, тобто  ,    

звідки  .   (5.2)

Умова перпендикулярності двох векторів.

Ненульові вектори  і  перпендикулярні тоді і тільки тоді, коли їхній скалярний добуток дорівнює нулю:

. (5.3)

Зокрема:  ,    ,    .

Вираз скалярного добутку через координати векторів та обчислення кута між векторами

Нехай вектори  і  задані своїми координатами

,      .

Тоді

                                                              (5.4)

Справді,

оскільки , ,  та .

Висновки з формули (5.4) такі:

1)   умова перпендикулярності векторів   і :

;

2)   довжина вектора : ;

3)   косинус кута між векторами   і :

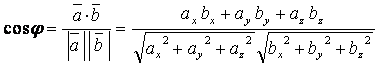
  Скалярное произведение

     Скалярное произведение векторов и :

где - угол между векторами и ; если либо , то

     Из определения скалярного произведения следует, что где, например, есть величина проекции вектора на направление вектора .

     Скалярный квадрат вектора:

     Свойства скалярного произведения:

     Скалярное произведение в координатах

     Если то

     Угол между векторами

     

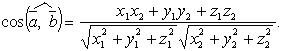
     Векторное произведение

     Векторное произведение векторов и - вектор, обозначаемый или для когорого:

     1) ( - угол между векторами и , );

     2)

     3) тройка , , - правая.

     Свойства векторного произведения: если , то равен площади параллелограмма, построенного на приведенных к общему началу векторах и .

72.

Загальне рівняння прямої

Загальне рівняння прямої лінії на площині в декартових координатах :

де A , B і C - Довільні постійні, причому постійні A і B не рівні нулю одночасно. Вектор з координатами (A, B) називається нормальним вектором і він перпендикулярний прямій. Вектор з координатами (-B, A) або (B,-A) називається направляючим вектором.

При C = 0 пряма проходить через початок координат. Також рівняння можна переписати у вигляді:

Нормальный вектор прямой - это любой ненулевой вектор, лежащий на любой прямой перпендикулярной данной.

Если в общем уравнении прямой

(1)

один или два из трех коэффициентов (считая и свободный член) обращаются в нуль, то уравнение называется неполным. Возможны следующие случаи:

1). С=0; уравнение имеет вид и определяет прямую, проходящую через начало координат.

2). В=0 (А 0); уравнение имеет вид и определяет прямую, перпендикулярную к оси Ох. Это уравнение может быть записано в виде х=а, где является величиной отрезка, который отсекает прямая на оси Ох, считая от начала координат.

3). В=0, С=0 (А 0); уравнение может быть записано в виде х=0 и определяет ось ординат.

4). А=0 (В 0); уравнение имеет вид и определяет прямую, перпендикулярную к оси Оу. Это уравнение может быть записано в виде y=b, где является величиной отрезка, который отсекает прямая на оси Оу, считая от начала координат.

5). А=0, С=0 (В 0); уравнение может быть записано в виде у=0 и определяет ось абсцисс.

Если ни один из коэффициентов уравнения (1) не равен нулю, то его можно преобразовать к виду

, (2)

где , суть величины отрезков, которые отсекает прямая на координатных осях.

Уравнение (2) называется уравнением прямой «в отрезках».

Если две прямые даны уравнениями

и ,

то могут представиться три случая:

а). - прямые имеют одну общую точку;

б). - прямые параллельны;

в). - прямые сливаются, то есть оба уравнения определяют одну и ту же прямую.