3.4. Геометрическое представление сигналов

Наряду с аналитическим представлением сигналов в теории связи активно используется геометрическое представление сигналов, когда каждый сигнал рассматривается как многокомпонентный вектор в многомерном функциональном пространстве. Подобный подход уже был использован в первой части книги при описании корректирующих кодов, однако, в силу специфики описания, в том случае рассматривались только дискретные векторные пространства. Здесь же речь пойдет об описании функций, могущих принимать континуальный набор значений.

Для произвольных сигналов s_r(t) и s_k(t) (r, k = 1, …, M), заданных на интервале [t₁; t₂] (могущим быть и бесконечным), вводится скалярное произведение, определяемое как

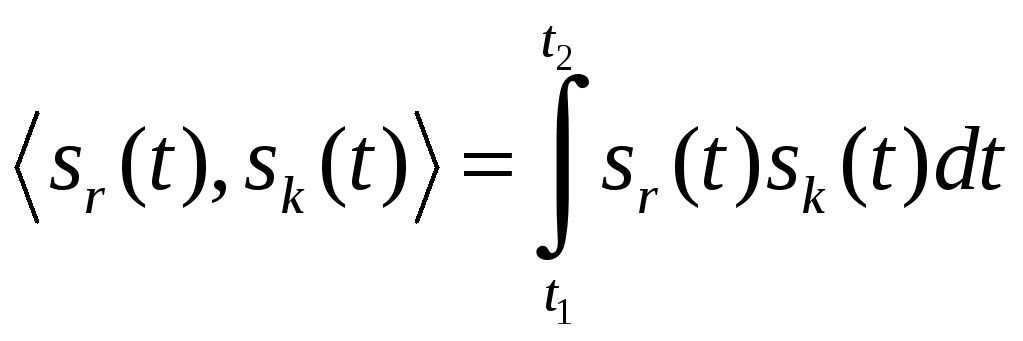. (3.39)

При этом если скалярное произведение равно нулю, то сигналы являются ортогональными. Норма сигнала равна

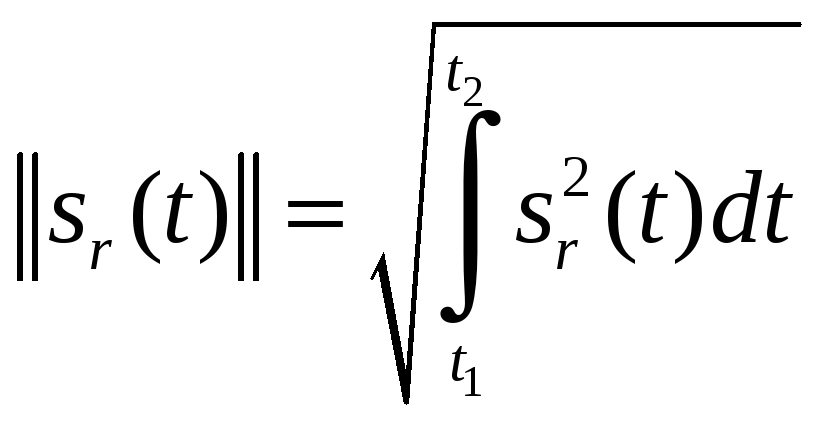. (3.40)

Ансамбль из M сигналов называется ортонормированным, если все сигналы попарно ортогональны, а их нормы равны 1.

Произвольный сигнал может быть представлен в виде разложения по совокупности {f_k(t)} ортонормированных сигналов (базису), т.е. таких, для которых

.

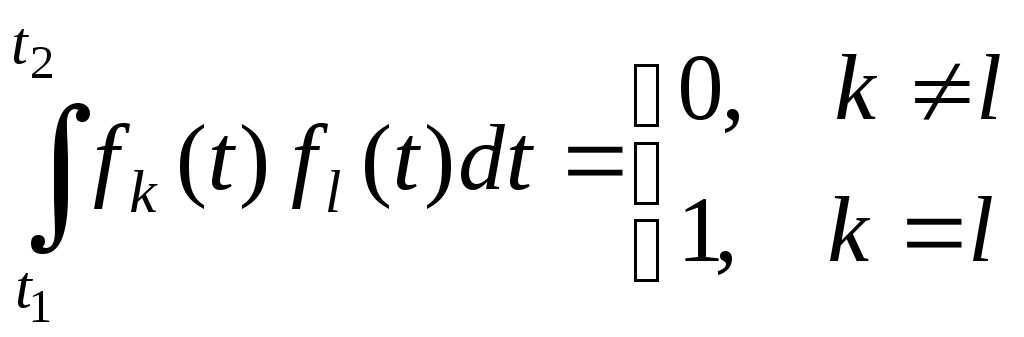При аппроксимации s(t) линейной комбинацией конечного числа ортонормированных сигналов:

коэффициенты c_k выбираются так, чтобы минимизировать среднеквадратическую ошибку аппроксимации

,

т.е. величину

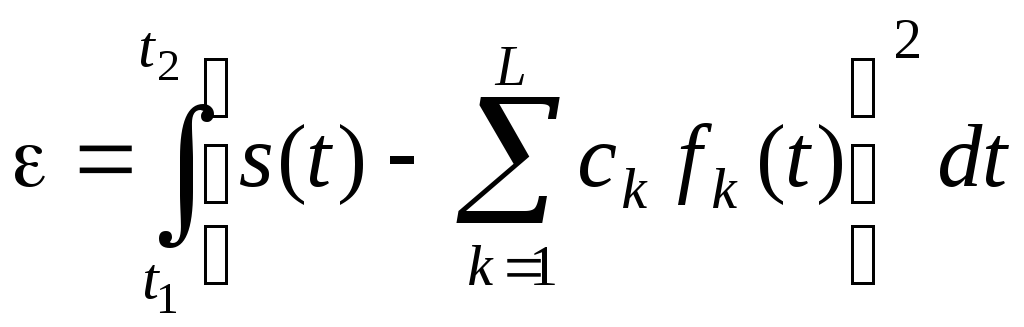. (3.41)

Дифференцируя (3.41) частным образом по каждому из коэффициентов c_k и приравнивая полученные производные нулю, получим, что

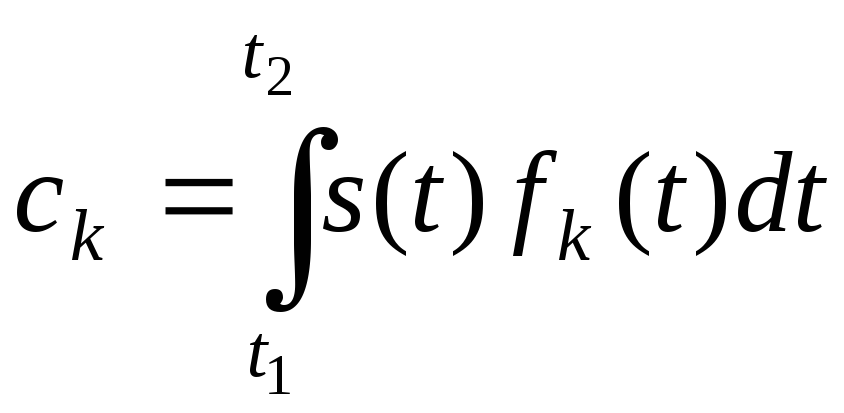. (3.42)

При этом минимальное значение среднеквадратической ошибки равно

,

где

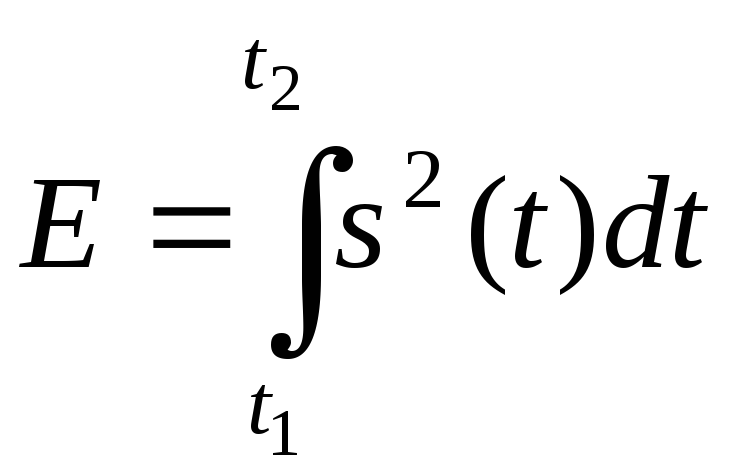
является энергией сигнала s(t). Если при L → ∞ среднеквадратическая ошибка стремится к нулю, то такая совокупность {f_k(t)} называется полной.

Примером разложения сигналов в ряд по системе ортонормированных сигналов является теорема отсчетов Котельникова – Найквиста, согласно которой любой сигнал с ограниченной полосой частот ΔF можно представить в виде

.

В данном случае в качестве базисных выступают функции

,

а интервал ортогональности составляет всю вещественную ось – ∞ < t < ∞.

Другим примером ортогонального разложения является разложение периодического на интервале [0; T] сигнала в ряд Фурье:

,

где коэффициенты разложения определяются как

.

Геометрическое представление сигналов позволяет ввести в рассмотрение удобный подход, заключающийся в том, что сигнал может быть описан набором ортогональных координат, полученных в процессе ортогонализации какого-либо ансамбля сигналов. Сама процедура ортогонализации известна еще с XIX в. и носит название процедуры Грама – Шмидта. Коротко опишем ее.

Упорядочим сигналы {s_k(t), k = 1, …, N} в исходном ансамбле произвольным образом и выберем в качестве первого члена ортонормированного набора сигнал

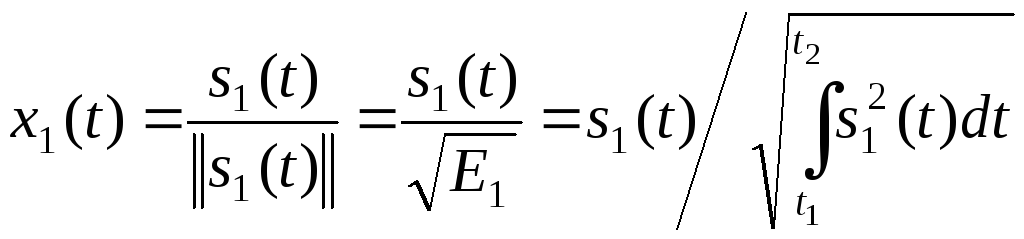, (3.43)

где E₁ – энергия сигнала s₁(t).

Далее, второй сигнал x₂(t) набора конструируется из уже построенного сигнала x₁(t), а также из исходного сигнала s₂(t). Для этого вычисляется коэффициент

,

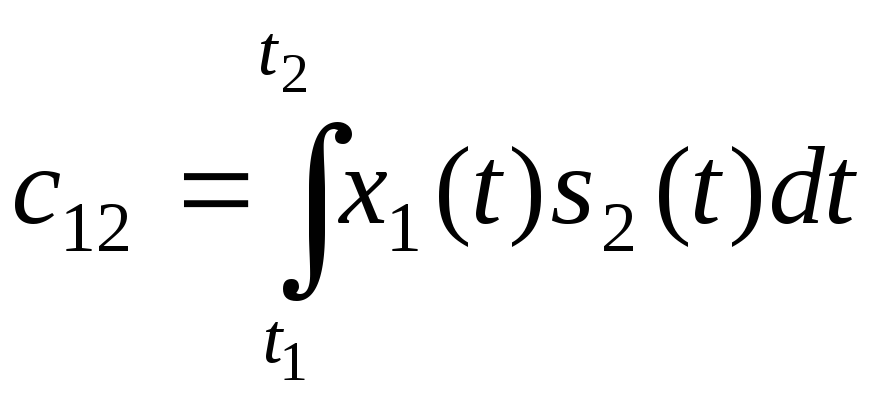после чего x₂(t) формируется как

. (3.44)

Нетрудно убедиться, что сигналы x₁(t) и x₂(t) ортогональны, поскольку их скалярное произведение (3.39) есть нуль.

Продолжая подобным образом процесс ортогонализации, имеем k-й сигнал (k = 1, …. M ≤ N), вычисляемый как

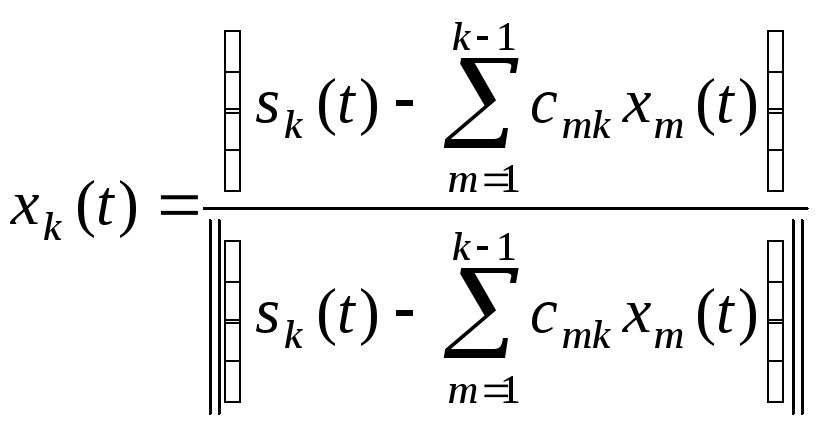, (3.45)

где

.

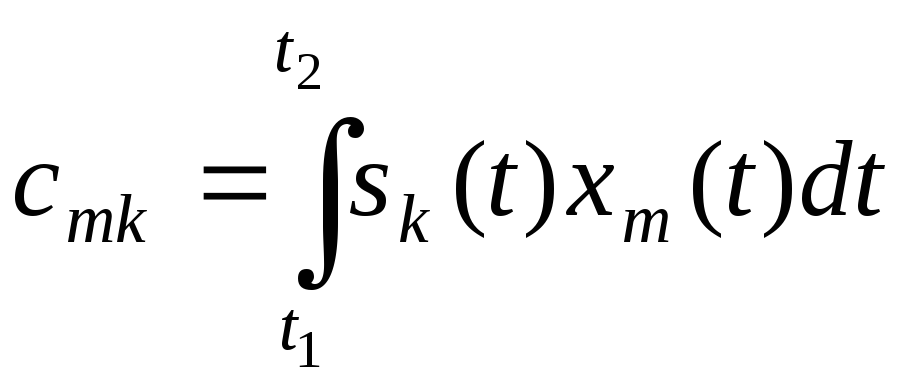При этом размерность M сигнального пространства будет равна N, если исходные сигналы линейно независимы, т.е. ни один из сигналов не является линейной комбинацией других сигналов.

Теперь, имея ортонормированный базис {x_k(t)}, можно выразить каждый сигнал s_k(t) как линейную комбинацию сигналов из этого базиса:

, , (3.46)

где s_kn, аналогично (3.39), вычисляется как

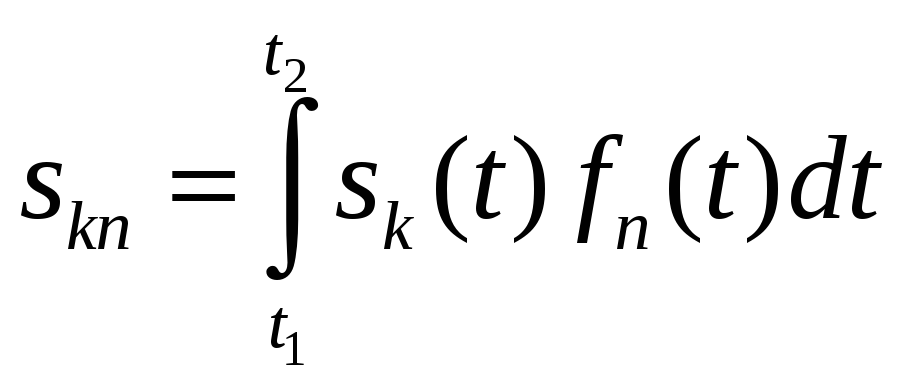. (3.47)

Таким образом, на основании выражения (3.46) каждый сигнал s_k(t) можно представить M-мерным вектором

, (3.48)

или, что эквивалентно, точкой в M-мерном сигнальном пространстве с координатами (3.48). Энергия такого сигнала равна квадрату длины вектора, т.е. квадрату эвклидова расстояния от начала координат к M-мерной точке.

Проиллюстрируем процедуру ортогонализации Грама – Шмидта и построение ортогональных координат на примере четырех сигналов, изображенных на рис. 3.13 [12].

Так как энергия s₁(t) равна , то первым в базисе является сигнал

.

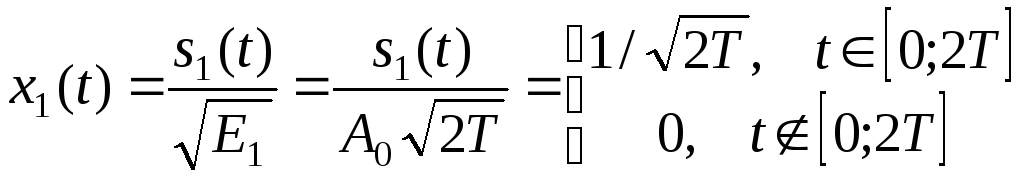Вычисление коэффициента c₁₂ показывает его нулевое значение, следовательно, сигналы s₂(t) и x₁(t) ортогональны, и

.

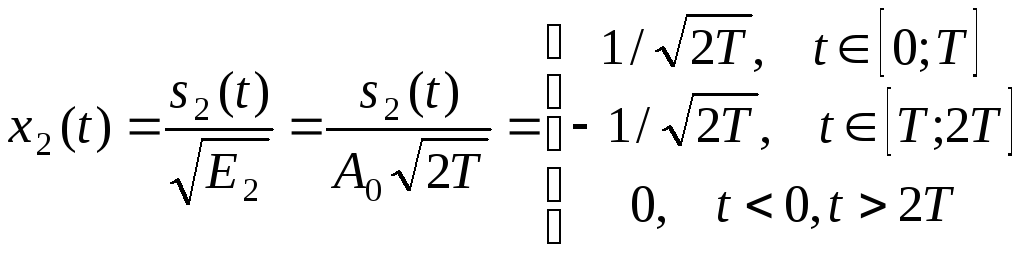Для получения x₃(t) вычисляем коэффициенты c₁₃ и c₂₃, которые оказываются равными c₁₃ = 0 и , поэтому

.

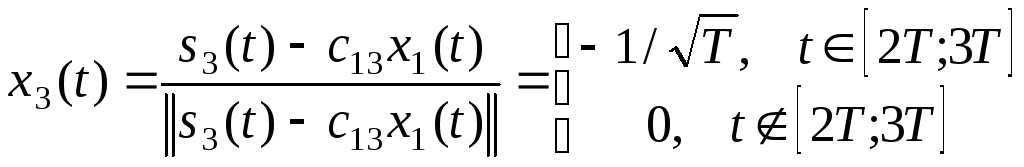Наконец, вычисляя , и , можно убедиться, что

,

т.е. набор сигналов s₁(t)–s₄(t) изначально был линейно зависимым. И действительно, нетрудно увидеть линейную связь

.

Полученный линейно независимый набор базисных сигналов x₁(t)–x₄(t) показан на рис. 3.14.

Теперь, опираясь на ортонормированный базис размерности M = 3, найдем ортогональные координаты рассматриваемых сигналов. Нетрудно видеть, что в данном случае векторное представление имеет вид

, ,

,

с соответствующими длинами

, , , .

Заметим, что базисные функции {x_k(t)}, полученные через процедуру Грама – Шмидта, не являются уникальными, поскольку изменяя порядок формирования ортонормированных сигналов, можно получить другой ортонормированный базис, а векторное представление (3.46) зависит от базисных функций.

Так, можно получить векторное представление

, ,

,

что соответствует базисным функциям, представленным на рис. 3.15. Однако это не влияет на длины векторов, которые являются инвариантными по отношению к выбору ортонормированного базиса.

Рассмотренный пример касался широкополосных сигналов, но не менее полезным геометрический подход оказывается и при рассмотрении узкополосных сигналов. Если записать модулированный сигнал s(t) на интервале [0; T] записать в комплексном виде (3.22), то можно заметить, что функции

и

являются ортонормированными базисными сигналами. Поэтому, записывая комплексную огибающую в виде

,

s(t) можно представить в виде разложения по базисным сигналам:

,

а ξ_с(t) и ξ_s(t) являются ортогональными координатами в таком разложении.

Фундаментальной характеристикой в пространстве сигналов является эвклидово расстояние Δ_mk между парой сигналов s_m(t) и s_k(t), определяемое как

,

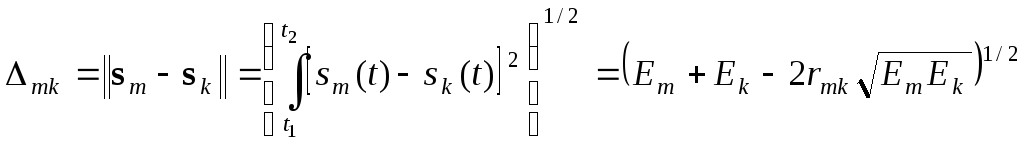где r_mk – коэффициент корреляции¹ сигналов, равный

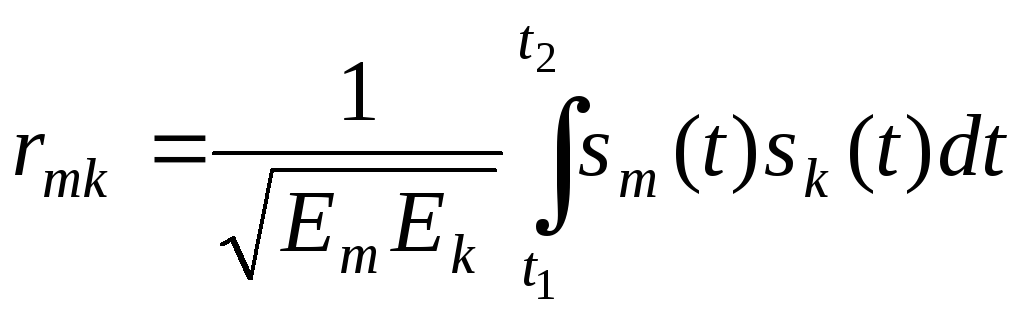. (3.49)

Эвклидово расстояние показывает, насколько близко или далеко координаты сигналы отстоят друг от друга в сигнальном пространстве и, в конечном итоге, определяет помехоустойчивость приема. Так например, при когерентном приеме в канале с аддитивным белым гауссовским шумом со спектральной плотностью средней мощности, равной N₀/2, средняя вероятность ошибки p для ансамбля из N сигналов может быть оценена сверху неравенством [9]

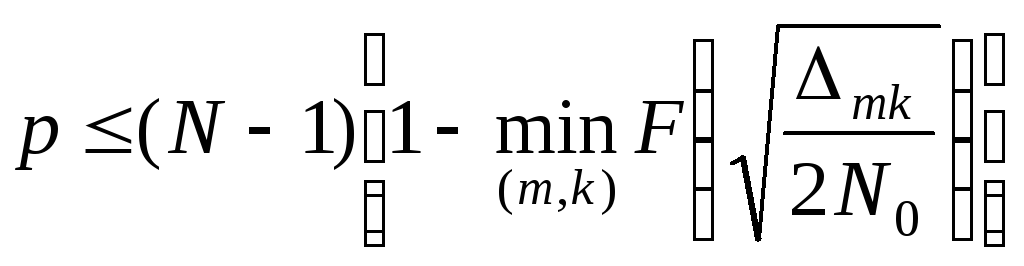, (3.50)

где – функция Лапласа.

При комплексном представлении сигналов можно ввести комплексный коэффициент корреляции (звездочка означает знак комплексного сопряжения)

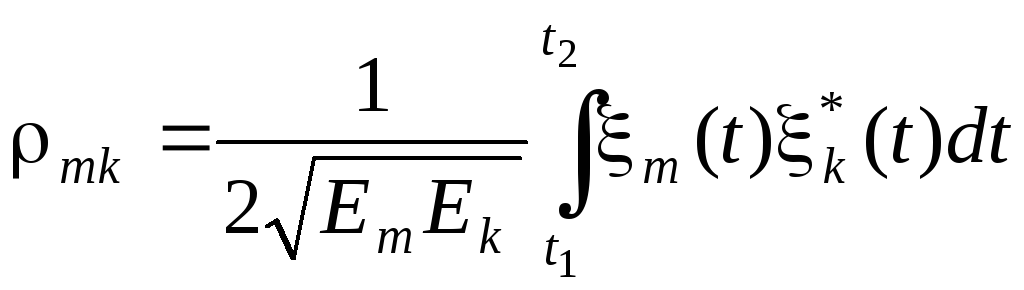, (3.51)

так что r_mk = Re[ρ_mk].