Волков А.Н., Попов Е.А., Сиверс М.А.

Физические основы мобильной связи.

Часть II. Оглавление

Оглавление 2

Глава 3. Методы модуляции сигналов в сспс 3

3.1. Спектральное представление сигналов 3

3.1.1. Спектр периодического сигнала 3

3.1.2. Спектр непериодического сигнала 6

3.1.3. Измерение спектров сигналов 10

3.1.4. Спектральные параметры сигналов 12

3.2. Модуляция сигналов 16

3.3. Комплексное представление сигналов 18

3.4. Геометрическое представление сигналов 23

3.5. Модуляция в цифровых системах мобильной связи 29

3.5.1. Фазовая манипуляция 30

3.5.2. Квадратурная амплитудная манипуляция 36

3.5.3. Модуляция непрерывной фазой 39

3.5.4. Ортогональное частотное разнесение 43

Литература 48

Глава 3. Методы модуляции сигналов в сспс

3.1. Спектральное представление сигналов

Основная идея спектрального подхода связана с желанием отказаться от представления сигналов с помощью непрерывных¹ функций, и вместо этого иметь возможность описывать процесс посредством задания конечного (желательно – малого) ряда параметров, а также набора функций, называемого базисом, известного во всех точках системы, где это необходимо. При этом указанный ряд параметров и называется спектром сигнала в заданном базисе. Примером спектрального представления сигналов является разложение в ряд Котельникова (см. выражение (2.1) в I части), при котором сигнал описывается набором своих отсчетных значений в базисе функций вида sin(x)/x. Однако, несмотря на теоретическую и практическую значимость такого разложения, оно не получило достаточно широкое распространение в качестве удобного средства описания сигналов, что, в первую очередь, связано со свойствами функций указанного базиса.

В настоящее время наиболее широко применяется спектральное представление в тригонометрическом базисе, математическим аппаратом которого является использование рядов и интегралов Фурье [2, 13]. При этом необходимо различать спектральное представление периодических и непериодических (случайных) сигналов. Следует заметить, что свойство периодичности понимается для бесконечного интервала времени –∞ < t < ∞, поэтому, строго говоря, в технических приложениях, в которых осуществляется передача информации за конечный временной промежуток, периодические сигналы применяться не могут. Однако если свойство периодичности выполняется на конечном интервале, существенно превышающем длительность характерных процессов, протекающих в системе, то для таких сигналов можно говорить как о периодических, в том смысле, что к ним применим соответствующий математический аппарат.

3.1.1. Спектр периодического сигнала

Если сигнал s(t) является периодическим с периодом T, то он может быть представлен в виде тригонометрического ряда Фурье:

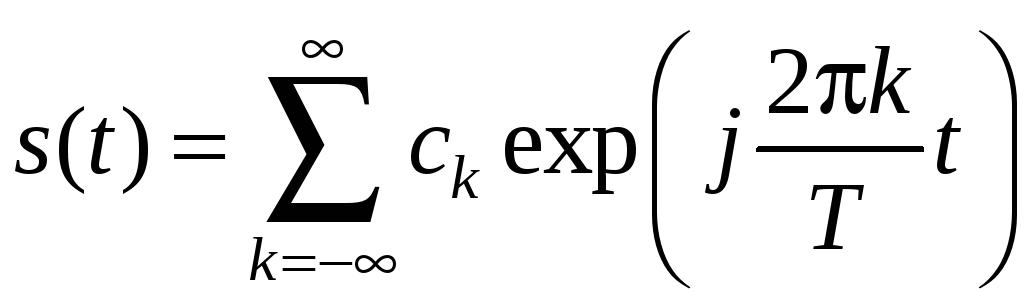, (3.1)

где c_k – коэффициенты Фурье, определяемые на интервале периодичности как

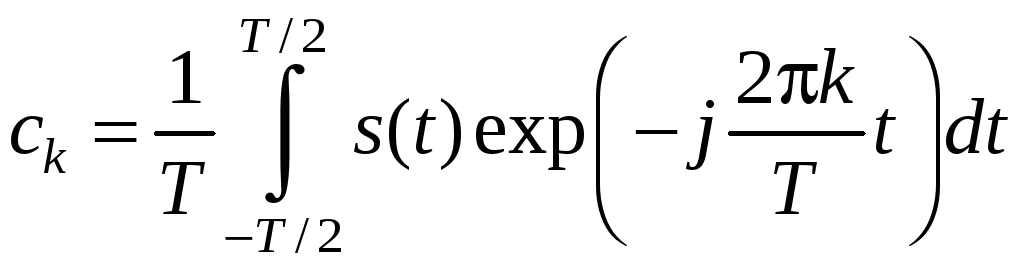. (3.2)

Совокупность коэффициентов {c_k} образуют спектр периодического сигнала в тригонометрическом базисе. Заметим, что, несмотря на то, что в правой части выражения (3.1) фигурируют комплексные величины, тем не менее, в силу определенной симметрии коэффициентов Фурье, а также свойств комплексных экспонент¹ в итоге получается вещественная функция. При этом c₀ представляет собой постоянную составляющую сигнала, c₁ и c_–1 определяют гармонику основного тона, а остальные коэффициенты c_k формируют гармоники высших порядков.

С практической точки зрения интерес представляет разложение (3.1) с конечным числом фигурирующих в сумме слагаемых:

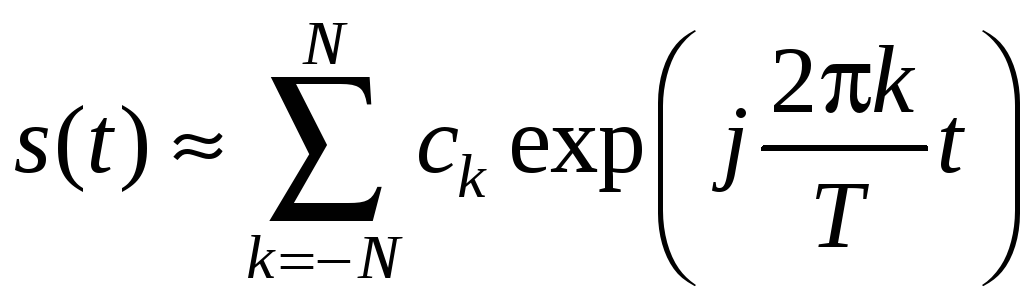, (3.2а)

причем количество N удерживаемых слагаемых, необходимое для представления сигнала s(t) с заданной точностью, определяется формой сигнала: чем более гладкой является форма s(t), тем меньшее число слагаемых требуется для его представления. Следовательно, наихудшими с этих позиций являются сигналы, форма которых имеет разрывы, например, последовательность прямоугольных импульсов, называемая меандром (рис. 3.1):

Рис. 3.1. Меандр и его аппроксимация тригонометрическими функциями

При аппроксимации меандра, например, пятью слагаемыми из выражения (3.2а) среднеквадратическая погрешность на интервале периодичности не превосходит 10%, однако в точках разрыва наблюдаются значительные выбросы, которые не могут быть ликвидированы даже при бесконечном числе слагаемых¹. Это явление, общее для всех разрывных функций, представляемых рядом Фурье, называется эффектом Гиббса. В то же время, если форма сигнала достаточно гладкая, то для удовлетворительного представления тригонометрическими слагаемыми достаточно ограничиться 3–5 слагаемыми. Так, уже для периодической последовательности треугольных импульсов при числе слагаемых N = 3 среднеквадратическая ошибка аппроксимации составляет менее 1%.

Спектральным коэффициентам можно придать ясный энергетический смысл. Если сигнал s(t) трактовать как напряжение или ток на нагрузке 1 Ом, то величина

(3.3)

представляет собой среднюю за период мощность сигнала, связанную с коэффициентами {c_k} соотношением

, (3.4)

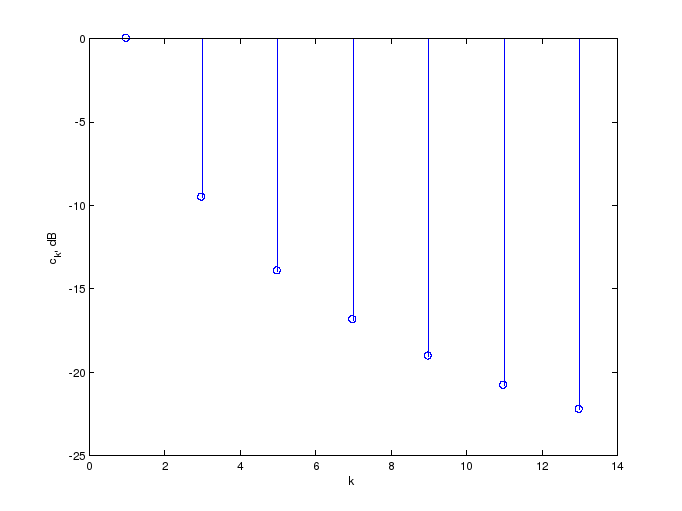
известным как равенство Парсеваля. Оно представляет собой распределение средней мощности сигнала по составляющим его гармоникам. Наглядное представление об этом дает графическое изображение амплитудных коэффициентов |c_k|. На рис. 3.2 приведен спектр показанного на рис. 3.1 меандра, при этом по оси абсцисс отложен номер гармоники (безразмерная величина k = f_kT), а по оси ординат – амплитуды гармоник |c_k|, измеряемые в децибелах, т.е. величины .

Рис. 3.2. Спектр периодического треугольного колебания

Как следует из приведенного на рис. 3.2 вида амплитудного спектра меандра, уровень 5-й гармоник относительно основного тона составляет –14 дБ. Аналогичное значение для периодической последовательности, например, треугольных импульсов равно –30 дБ. Заметим, что отсутствие (равенство нулю) четных гармоник является спецификой данного примера и не отражает общих особенностей спектра периодических колебаний.