3.3. Комплексное представление сигналов

Как известно, при решении многих задач теории цепей удобно вместо гармонического сигнала x(t) вида (3.16) рассматривать комплексный сигнал z(t) или его комплексную амплитуду A = A₀exp(jφ). Такой метод решения задач носит название метода комплексных амплитуд.

Обобщением метода комплексных амплитуд в теории сигналов является представление модулированного колебания x(t) в виде вещественной части некоторого комплексного сигнала

z(t) = x(t) + jy(t), (3.22)

где y(t) – вообще говоря, однозначно не определенный, так называемый сопряженный сигнал. Переписав (3.22) в экспоненциальной форме

, (3.23)

где

, ,

можно затем определить вещественную огибающую сигнала

, (3.24)

его полную мгновенную фазу

(3.25)

и мгновенную частоту

. (3.26)

Наконец, задавшись некоторой средней частотой ω₀ и определив мгновенную начальную фазу

, (3.27)

можно записать исходный сигнал x(t) в форме

, (3.28)

где – комплексная огибающая сигнала.

Заметим, что мгновенная начальная фаза φ(t) и комплексная огибающая ξ(t) даже при заданном y(t) определены неоднозначно, поскольку они зависят от произвольно задаваемой средней частоты ω₀, но вещественная огибающая A(t), мгновенная частота ω(t) и полная мгновенная фаза Φ(t) полностью определяются x(t) и y(t) согласно формулам (3.24)–(3.26). Таким образом, проблема однозначного определения огибающей и фазы сигнала сводится к определению сопряженного сигнала y(t) по известному сигналу x(t).

В большинстве литературы, посвященной цифровой связи, в качестве сигнала y(t) выбирают сигнал, сопряженный с x(t) по Гильберту, т.е. являющийся преобразованием Гильберта¹ от x(t):

. (3.29)

Физическая сущность преобразования Гильберта заключается в повороте фаз всех спектральных составляющих на –π/2 в области положительных частот и на π/2 в области отрицательных частот, т.е. если S_x(ω) – преобразование Фурье сигнала x(t), то преобразование Фурье сигнала, сопряженного по Гильберту, равно

. (3.30)

В результате спектр (преобразование Фурье) комплексного сигнала z(t) оказывается целиком сосредоточен в области положительных частот, поскольку

. (3.31)

Иными словами, вещественный сигнал x(t) может быть однозначно выражен с помощью комплексного сигнала x₊(t), спектр которого тождественно отличен от нуля лишь при ω > 0 и совпадает в этой области со спектром сигнала x(t). Имеем:

, (3.32)

, (3.33)

откуда

. (3.34)

Таким свойством с математической точки зрения обладают аналитические функции, поэтому сигнал z(t) часто называют аналитическим сигналом, а вещественную огибающую A(t) – гильбертовской огибающей.

Выбор в качестве сопряженного сигнала преобразования Гильберта приводит к ряду интересных свойств, оправдывающих его использование в телекоммуникационных системах и вообще в цифровой обработке сигналов [8], например:

• гильбертовская огибающая A(t) для гармонического сигнала совпадает с амплитудой A₀, а мгновенная частота ω(t) – с круговой частотой ω₀;

• малым (в смысле среднеквадратического отклонения) изменениям сигнала x(t) соответствуют малые изменения A(t) и ω(t);

• при умножении аналитического гильбертовского сигнала на фазовый сдвиг exp(jψ), где ψ – произвольный угол, то результирующий сигнал остается гильбертовским;

• для относительно узкополосного сигнала

его преобразование Гильберта имеет вид

,

т.е. отличается заменой синуса на косинус.

В качестве примера использования введенного понятия гильбертовской огибающей рассмотрим связь формы относительно узкополосного радиосигнала s(t) с формой модулирующего сигнала g(t) для некоторых практически интересных случаев [11].

При амплитудной модуляции

(3.35)

согласно перечисленным выше свойствам преобразование Гильберта дает

,

поэтому гильбертовская огибающая имеет вид

,

т.е. фактически повторяет форму модулирующего напряжения.

При балансной модуляции

, (3.36)

откуда

и

,

т.е. огибающая, вообще говоря, существенно отличается от модулирующего сигнала g(t), хотя и связана с ним простой зависимостью.

Весьма интересным получается результат для случая однополосной модуляции, когда результирующее колебание получается из балансномодулированного колебания посредством удаления (фильтрации) одной из боковых частот¹.

Пусть спектр S_g(ω) исходного модулирующего сигнала g(t) сосредоточен в области частот , определяемой, например, по критерию концентрации энергии. Получим сигнал с балансной модуляцией вида (3.36) и представим его в форме

.

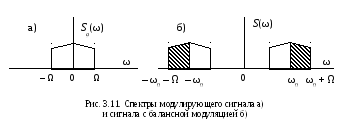
Спектр такого сигнала, очевидно, равен

и состоит из двух симметрично расположенных (относительно частот ω = ±ω₀) боковых полос, как это условно показано на рис. 3.11. Спектр S_OM(ω) искомого сигнала с однополосной модуляцией может быть получен фильтрацией одной из боковых полос. Так, для верхней боковой полосы (отмеченной на рис. 3.11 штриховкой) имеем:

.

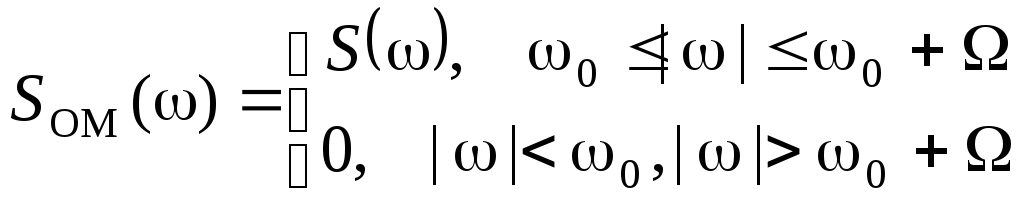Вычисляя обратное преобразование Фурье от спектра S_OM(ω), получим выражение для сигнала s_OM(t) с однополосной модуляцией:

.

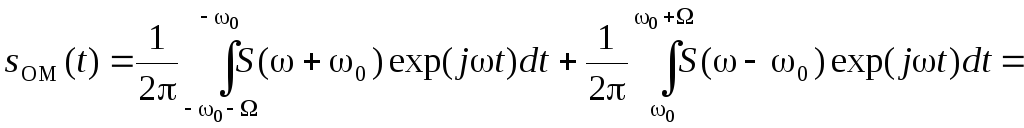
Распространяя формально пределы интегрирования до бесконечности и вводя сигналы x(t) и x₊(t) согласно (3.32) и (3.33), получим

.

Комплексный сигнал x₊(t) – аналитический, т.е. его вещественная и мнимая части являются сопряженными по Гильберту, поэтому окончательно имеем:

.

Найдем гильбертовскую огибающую такого сигнала. Так как

,

то выражение для огибающей сигнала с однополосной модуляцией имеет вид:

. (3.37)

Как следует из последнего соотношения, форма огибающей однополосного сигнала существенно отличается от формы модулирующего сигнала g(t) и совпадает с формой огибающей последнего. В частности, при тональной модуляции, т.е. модуляции гармоническим колебанием с частотой Ω, огибающая однополосного сигнала имеет постоянное значение.

Однако, следует отметить, что использование гильбертовского сопряжения оказывается удобным и оправданным лишь для относительно узкополосных сигналов, т.е. для тех, у которых полоса частот существенно меньше, чем центральная частота ω₀. Попытка применения преобразования Гильберта к широкополосным, в частности, к видеосигналам может привести к тому, что гильбертовская огибающая A(t) будет существенно отличаться от огибающей, понимаемой в интуитивном смысле. В частности, может оказаться нефинитной, иметь значительные выбросы и др.

В качестве примера найдем гильбертовскую огибающую видеосигнала с прямоугольной формой: s(t) равно постоянному значению A₀ при – T/2 ≤ t ≤ T/2 и равно нулю вне этого интервала. Поскольку

,

огибающая сигнала имеет вид

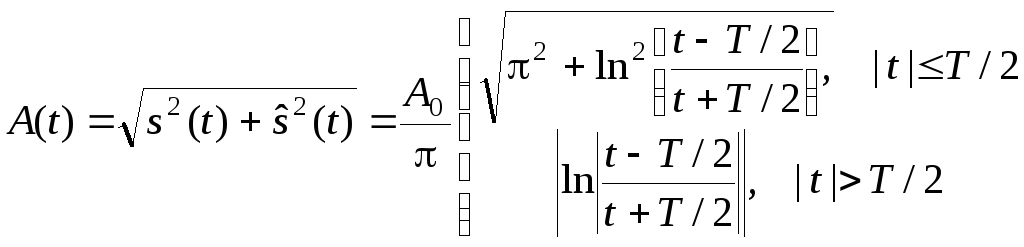. (3.38)

На рис. 3.12 показан вид нормированной огибающей A(t)/A₀, а также вещественная и мнимая составляющие аналитического сигнала. Видно, что в точках t = ±T/2 возникают бесконечные выбросы огибающей. На практике такие выбросы, разумеется, имеют конечные значения (идеальный фазовращатель практически реализовать невозможно), но, как правило, они существенно превышают значения исходного сигнала. Тем не менее, в теории и технике связи не отказываются от широкого использования преобразования Гильберта, в том числе и для широкополосных сигналов, поскольку применение этого понятия позволяет построить эффективную теорию модуляции и оптимального приема [10].