3.5.3. Модуляция непрерывной фазой

Как уже было отмечено выше при использовании сигналов с фазовой манипуляцией, как с постоянной огибающей, так и с КАМ, в приемо-передающих трактах с частотно-избирательными цепями (что практически всегда имеет место) возможно возникновение нежелательных провалов огибающей в момент перескока фазы. Данное паразитное явление можно несколько снизить, применяя манипуляцию со сдвигом, однако кардинально решить проблему при этом все же не удается.

Принципиально иным решением данной проблемы является отказ от систем с фазовой манипуляцией (т.е. со скачкообразным изменением значений фаз) и переход к сигналом, имеющих непрерывные фазовые траектории. Системы, в которых передача информации осуществляется таким образом, называются системами с модуляцией непрерывной фазой (МНФ).

N-элементную последовательность сигналов с МНФ, с помощью которых передается последовательность символов , d_r = m – 2r + 1, r = 1, …, m, можно записать в виде

. (3.69)

В данном выражении фазовая траектория

(3.70)

определяется набором h = [h₁, …, h_L] значений индексов модуляции, вообще говоря, меняющихся при переходе от одного тактового интервала к другому, и видом фазового импульса q(t) или частотного импульса g(t), связанного с фазовым интегральным соотношением

. (3.71)

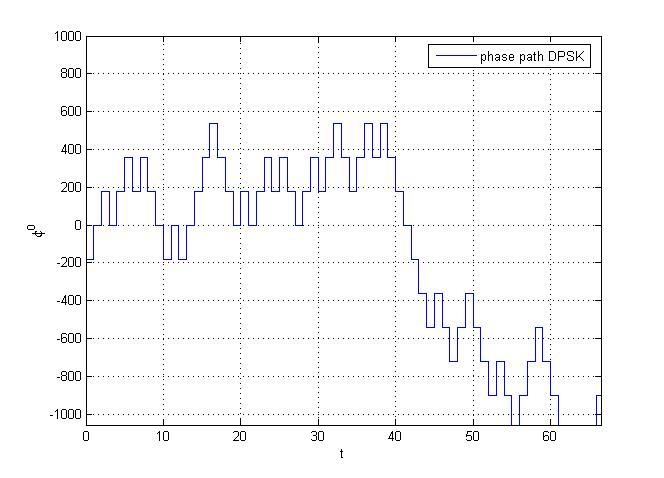
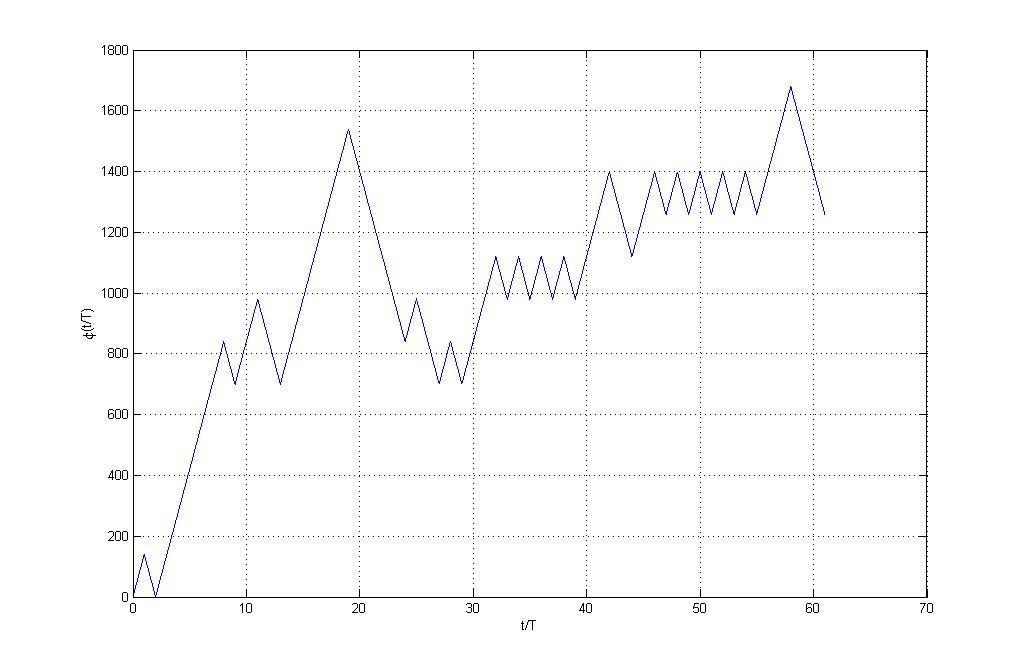
На рис. 3.21 показаны фазовые траектория для двух видов фазовой модуляции: ФМ-2 (а) и ЧМНФ-2 с частотным импульсом прямоугольной формы и одним значением индекса модуляции (б).

Заметим, что наряду с прямоугольной, используются и другие формы частотного импульса, например, в виде так называемого “приподнятого косинуса”:

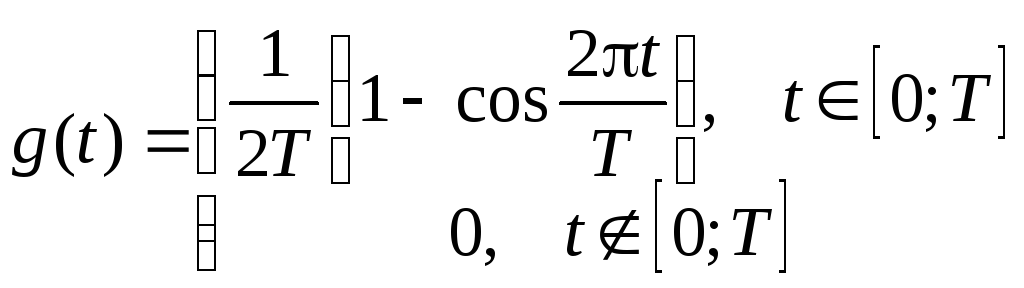. (3.72)

Кроме того, в последнее время все большее распространение получают сигналы с ЧМНФ и парциальным откликом, когда длительность частотного импульса составляет несколько тактовых интервалов. Использование сигналов с парциальным откликом позволяет повысить спектральную эффективность сигналов, но несколько снижает их помехоустойчивость и существенно усложняет реализацию приемных устройств.

а)	б)
Рис. 3.21. Фазовые траектории для ФМ-2 (а) и двоичной ЧМНФ с прямоугольным частотным импульсом (б)

Одной из наиболее часто используемых разновидностей МНФ является частотная модуляция с минимальным сдвигом частоты (ММС), при которой выбираются двоичные символы d_r (r = 1,2), прямоугольная форма частотного импульса на интервале [0; T] и значение индекса модуляции, одинаковое на всех тактовых интервалах и равное 1/2. Для произвольного k-го тактового интервала [kT; (k + 1)T] фазовая траектория при ММС имеет вид

, (3.73)

а модулированный сигнал равен

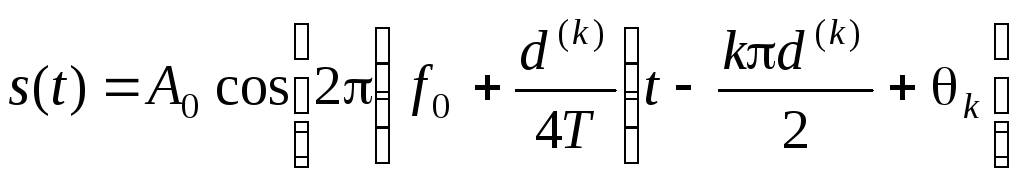, (3.74)

где – набег фазы, предшествующий k-му тактовому интервалу.

Запись сигнала с ММС в форме (3.74) указывает на возможность его трактовки как отрезка гармонического колебания, имеющего на интервале [kT; (k + 1)T] одно из двух возможных значений частоты:

или . (3.75)

Записывая возможные сигналы как

, r = 1,2, (3.76)

можно увидеть, что частотный разнос составляет Δf = f₁ – f₂ = 1/(2T) – минимальное значение, при котором соответствующие сигналы s₁(t) и s₂(t) будут ортогональны. Это и объясняет, почему двоичную МНФ с h = 1/2 называют модуляцией с минимальным сдвигом частоты.

Представление модулированных сигналов в виде суммы квадратурных составляющих является удобным для оценки их спектральных свойств. При этом симметричный спектр каждой составляющей определяется односторонним спектром модулирующего сигнала, а результирующий спектр равен сумме спектров квадратурных составляющих. Так например, для сигналов КФМ и КФМС энергетический спектр имеет вид

, (3.77)

а для сигналов с ММС –

, (3.78)

где определяет отклонение текущей частоты спектра от центральной частоты ω₀.

Как было указано разд. 3.1.4, компактность спектра удобно характеризовать концентрацией энергии η(E) в заданной полосе частот F, симметрично расположенной относительно центральной частоты спектра. В табл. 3.5 даны процентные значения η(E) для различных методов модуляции в зависимости от нормированной полосы частот FT и, обратно, значения нормированной полосы в зависимости от концентрации энергии

Таблица 3.5.
Вид модуляции	η(E), % при различных FT			FT при различных η(E), %
	1,00	1,25	1,50	90,0	95,0	97,0	99,0	99,9
КФМ, КФМС	90,5	91,2	93,0	0,85	1,95	3,45	6,20	9,60
ММС	97,0	99,3	99,5	0,78	0,91	1,00	1,18	2,60

Из представленных в табл. 3.5 данных видно, что в полосе FT = 1 (ее обычно называют полосой Найквиста) сигналы с ММС характеризуются наиболее компактным спектром. Тем не менее, такое сравнительное лидерство является недостаточным с точки зрения современных требований к электромагнитной совместимости, и для того, чтобы сигналы с ММС могли быть использованы в современных телекоммуникационных системах, они должны быть подвергнуты дополнительному сужению спектра с помощью фильтрации.

В мобильной связи (GSM, TETRA, DECT) наибольшее распространение получил подход, при котором в качестве параметрической амплитудной частотной характеристики фильтра выбирается гауссовская кривая

, (3.79)

где a – параметр фильтрации, поэтому соответствующие сигналы называются гауссовскими сигналами с минимальным сдвигом частоты (ГММС). Часто вместо параметра a рассматривается полоса пропускания фильтра Π по уровню 3 дБ; указанные параметры связаны соотношением

. (3.80)

Если на вход такого фильтра подается сигнал x(t) = rect(t, T) прямоугольной формы, единичной амплитуды и длительностью T, то на выходе фильтра он имеет вид [18]

, (3.81)

где .

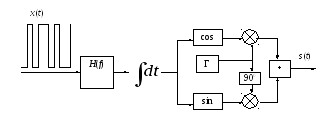
На рис 3.22. показана структурная схема модулятора ГММС, который, по сути, является квадратурным модулятором ММС с добавленным гауссовским фильтром.

На вход модулятора подаются двоичные сигналы фазовой траектории x(t) в форме прямоугольных частотных импульсов, полярность которых отражает поступление логического нуля или единицы. После гауссовской фильтрации и интегрирования происходит раздельное формирование квадратурных компонент и далее, с помощью опорного генератора несущей частоты ω₀ и квадратурного сумматора – формирование результирующего сигнала s(t). Заметим, что реализация модулятора осуществляется цифровыми методами и, в частности, частотная характеристика гауссовского фильтра должна быть аппроксимирована характеристиками цифровых БИХ- или КИХ-фильтров¹. При этом необходимо обеспечить адекватность аппроксимирующей характеристики цифрового фильтра выражению (3.79).

Рис. 3.22. Структурная схема модулятора ГММС

Применение гауссовского фильтра позволяет получить семейство сигналов с ГММС, различающихся как занимаемой полосой частот, так и помехоустойчивостью. Понятно, что с ростом a (с уменьшением Π) повышается интенсивность фильтрации, т.е. подавление внеполосных излучений, однако при слишком больших a (слишком малых Π) из-за чрезмерного растягивания частотных импульсов происходит их наложение друг на друга – так называемая межсимвольная интерференция. Как следствие, помехоустойчивость приема заметно снижается.

Основным параметром, определяющим выбор конкретного типа сигнала с ГММС, является произведение ΠT, где T – длительность, соответствующая передаче одного бита сообщения. Спектр, для которого ΠT = 0,3 соответствует сигналам, используемых в сотовых сетях мобильной связи стандарта GSM. Напомним, что в этом случае T = 3,69 мкс, и при выборе ширины канала Δf = 200 кГц может быть обеспечена скорость передачи B = 271 кбит/с (не следует путать со скоростью передачи полезной информации). В стандарте DECT выбрано значение ΠT = 0,5, и это позволяет организовать в полосе 1,725 МГц передачу информации со скоростью 1152 кбит/с.