Холостой ход

При холостом ходе линии (I2 = 0)

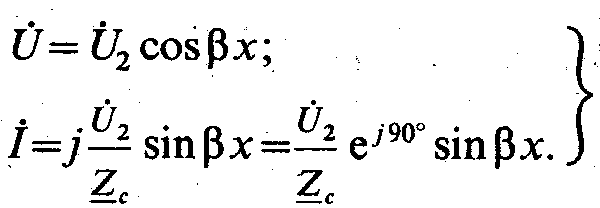
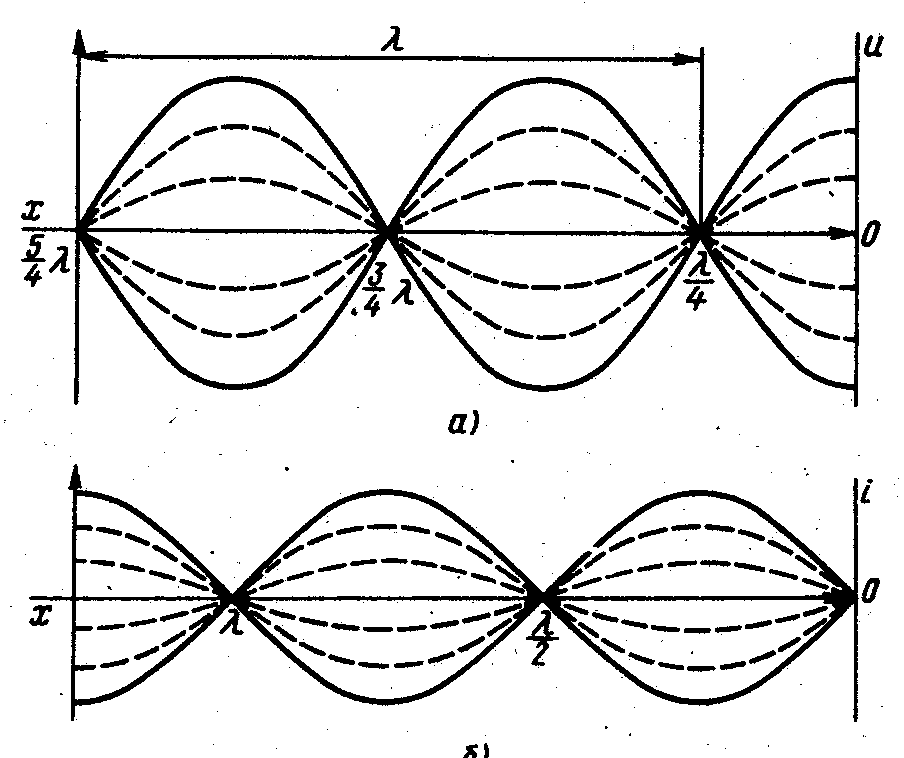
Напряжение и ток вдоль линии в любой момент времени распределены по синусоидальному закону, причем. в пунктах, где напряжение равно нулю, ток имеет наибольшую величину, а в пунктах с наибольшим напряжением ток равен нулю (рис. 26.6, а, б).

Точки линии, в которых напряжение или ток равны нулю, называются узлами, а точки с наибольшей величиной напряжения или тока — пучностями.

Таким образом, узлы напряжения по месту расположения на линии совпадают с пучностями тока, а пучности напряжения — с узлами тока.

Положение узлов напряжения и пучностей тока найдем, приравняв нулю напряжение в первом уравнении (26.14): U = 0 при β х = k+π/2, где k—любое целое число или нуль, т. е.

при β х = π/2, 3 π/2, 5 π/2 и т.д.

Положение на линии узлов тока и пучностей напряжения определяется из второго уравнения (26.14) при I= 0.

Напряжение и ток, распределяясь вдоль линии по синусоидальному закону без затухания, по такому же закону изменяются во времени.

Короткое замыкание

Аналогичная картина наблюдается и при коротком замыкании конца линии без потерь Отличие электромагнитных процессов в линии без потерь в режимах холостого хода и короткого замыкания состоит лишь в том, что изменяется расположение пучностей и узлов напряжения и тока по длине линии: в тех пунктах, где при холостом ходе находятся пучности напряжения и узлы тока, при коротком замыкании обнаруживаются пучности тока и : узлы напряжения. В частности, в конце разомкнутой линии имеется пучность напряжения и узел тока (I2 = 0), а в конце короткозамкнутой линии имеются пучность тока и узел напряжения (U2=0).

Стоячая волна

Пусть вектор напряжения в конце разомкнутой линии направлен по действительной оси комплексной плоскости, т. е. начальная временная фаза напряжения равна нулю:

В этом случае мгновенные значения напряжения и тока в линии можно выразить. уравнениями

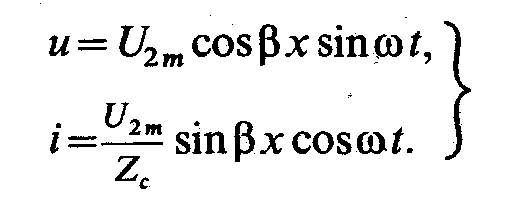
При ωt = 0 во всех точках линии напряжение отсутствует (u = 0). Затем напряжение растет во всех пунктах линии, кроме узлов, и при ωt = π/2 достигает амплитуды.

Но эта амплитуда напряжения во всех пунктах линии разная. В месте пучности напряжение достигает наибольшего значения U2m а в узле оно всегда равно нулю.

Электромагнитный процесс, подчиняющийся уравнениям (26.15), называется стоячей волной, характерной особенностью которой является неподвижность узлов и пучностей на линии.

Бегущая волна

Из тригонометрии известно, что

Следовательно, напряжение и ток в линии можно представить суммой двух составляющих, каждая из которых является уравнением бегущей волны:

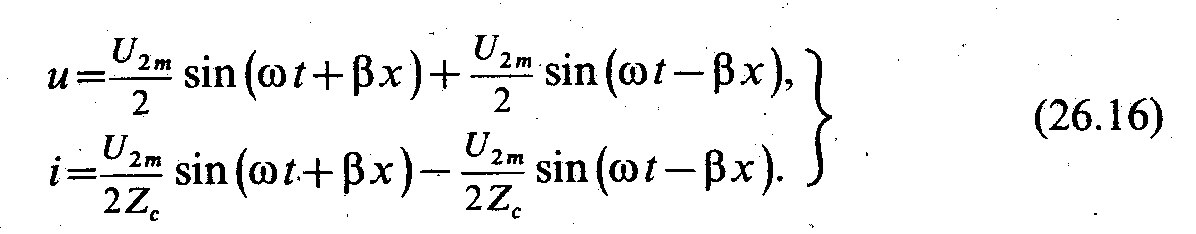
Первое слагаемое в этих уравнениях — прямая волна, распространяющаяся от начала к концу линии; второе — обратная волна с такой же амплитудой.

В этом можно убедиться, рассмотрев подробно одну из составляющих, например первую в уравнении напряжения.

Предположим, что некоторая величина напряжения u’ в момент времени t имеет место в пункте, пространственное положение которого определяется расстоянием х от конца (или начала) линии (см. рис. 26.5)

Распространение волны напряжения означает, что через бесконечно малый промежуток времени dt такое же напряжение u’ возникает в другом пункте линии, отстоящем от первого на бесконечно малое расстояние dх:

Равенство напряжений в моменты времени, отстоящие на dt, возможно при равенстве аргументов синусов в обоих уравнениях, т. е. при

Отсюда

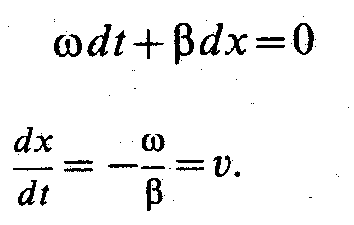
Отношение dx/dt характеризует скорость распространения волны напряжения вдоль линии и называется фазовой скоростью волны.

Знак минус указывает на то, что волна движется от начала к концу линии (расстояние х уменьшается).

Аналогично можно показать, что вторая составляющая напряжения в уравнении (26.16) представляет собой волну, распространяющуюся в обратном направлении (х увеличивается).

Волна, распространяющаяся от начала к концу линии, называется прямой или падающей, а волна, распространяющаяся в обратном направлении (от конца линии к началу), — обратной или отраженной.

Те же рассуждения можно отнести к составляющим тока во втором уравнении (26.16).

Таким образом, стоячая волна напряжения представляет собой сумму, а волна тока —-разность прямой (падающей) и обратной (отраженной) волн одинаковой амплитуды.