Тема 1.4 Основы расчета электрических цепей постоянного тока

Разветвленные цепи. Законы Кирхгофа. Режимы работы источников питания.

Обобщенный закон Ома позволяет рассчитать практически любую слож­ную цепь. Однако непосредственный расчет разветвленных цепей, содержащих несколь­ко замкнутых контуров (контуры могут иметь общие участки, каждый из контуров может иметь несколько источников тока и т. д.), довольно сложен. Эта задача решает­ся более просто с помощью двух правил Кирхгофа.

Любая точка разветвления цепи, в которой сходится не менее трех проводников с током, называется узлом. При этом ток, входящий в узел, считается положительным, а ток, выходящий из узла, — отрицательным.

Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:

Например, для рис. 148 первое правило Кирхгофа запишется так:

П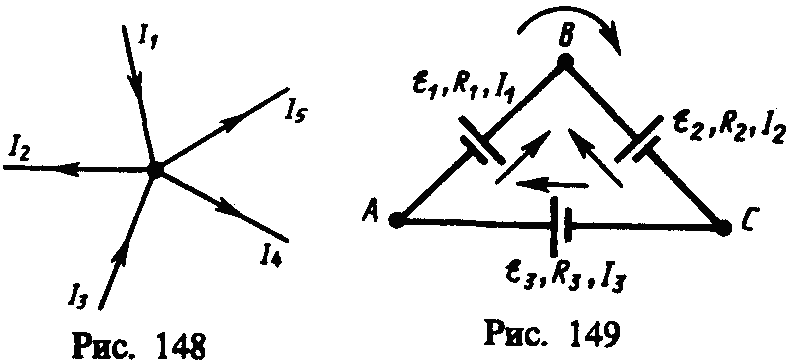ервое правило Кирхгофа вытекает из закона сохранения электрического заряда. Действительно, в случае установившегося постоянного тока ни в одной точке провод­ника и ни на одном его участке не должны накапливаться электрические заряды. В противном случае токи не могли бы оставаться постоянными.

Второе правило Кирхгофа получается из обобщенного закона Ома для разветвлен­ных цепей. Рассмотрим контур, состоящий из трех участков (рис. 149). Направление обхода по часовой стрелке примем за положительное, отметив, что выбор этого направления совершенно произволен. Все токи, совпадающие по направлению с напра­влением обхода контура, считаются положительными, не совпадающие с направлением обхода — отрицательными. Источники тока считаются положительными, если они создают ток, направленный в сторону обхода контура. Применяя к участкам закон Ома, можно записать:

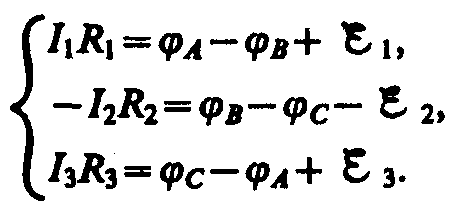
Складывая почленно эти уравнения, получим

(101.1)

Уравнение (101.1) выражает второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов I_i на сопротивления R_i соответствующих участков этого контура равна алгебраической сумме э.д.с. , встречающихся в этом контуре:

(101.2)

При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо:

1. Выбрать произвольное направление токов на всех участках цепи; действительное направление токов определяется при решении задачи: если искомый ток получится положительным, то его направление было выбрано правильно, отрицательным — его истинное направление противоположно выбранному.

2. Выбрать направление обхода контура и строго его придерживаться; произведе­ние IR положительно, если ток на данном участке совпадает с направлением обхода, и, наоборот, э.д.с., действующие по выбранному направлению обхода, считаются поло­жительными, против — отрицательными.

3. Составить столько уравнений, чтобы их число было равно числу искомых величин (в систему уравнений должны входить все сопротивления и э.д.с. рассматрива­емой цепи); каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержащийся в предыдущих контурах, иначе получатся уравнения, являющиеся простой комбинацией уже составленных.

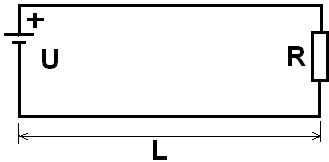
Расчет проводов на потери напряжения

Соединение источников тока

Пусть n источников тока соединены последовательно и замкнуты на внешнюю цепь (R)

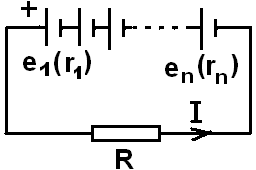
Обозначим ЭДС каждого источника е_1, его внутреннее сопротивление – r₁, а сопротивление внешней цепи – R.

Тогда второе правило Кирхгофа дает:

I(n r₁ + R) = n е₁

Сравнивая эту формулу с законом Ома для замкнутой цепи, видим, что батарея действует как один источник тока, у которого ЭДС и внутреннее сопротивление имеют значения:

е = е₁; r = n r₁.

При последовательном соединении n одинаковых источников тока ЭДС батареи её внутреннее сопротивление в n раз больше, чем у одного источника.

Параллельное соединение источников тока показано на рисунке.

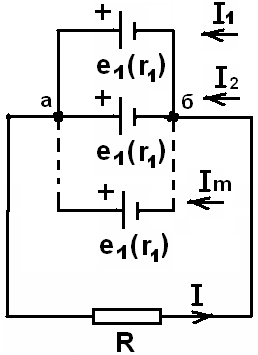
e₁ = e₂ = … = e_m = e

r₁ = r₂ = … = r_m = r

В этом случае все положительные полюсы отдельных источников соединены между собой и образуют два полюса (а и б) батареи.

Выбрав положительное направление токов и применив оба правила Кирхгофа получим для общей цепи:

I = I₁ + I₂ + …+ I_m ,

I(R + r₁/m) = e₁.

Отсюда видно, что такая батарея действует как один источник тока для которого е = e₁ ; r = r₁.

Смешанное соединение источников тока показано на следующем рисунке

Т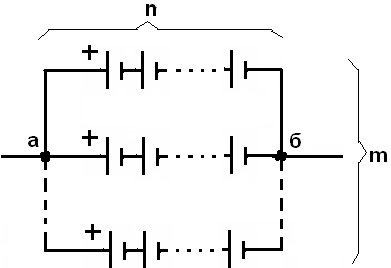акая батарея состоит из m параллельно соединенных звеньев, в каждом из которых содержится n последовательно соединенных источников тока.

ЭДС и внутреннее сопротивление этой батареи имеют значения:

e = n_*e₁ ; r = r_{1 *} n/m

Литература:

1. Жаворонков М.А., Кузин А.В. Электротехника и электроника. Москва,

АСАДЕМ!А, 2005.

2. Касаткин А.С., Немцов М.В. Электротехника. Москва, Высшая школа, 2003

3. Петленко Б.И. Электротехника и электроника. Москва,

АСАДЕМ!А, 2004.

4. Шихин А.Я. Электротехника. Москва, Высшая школа, 2001

5. Берикашвили В.Ш., Черепанов А.К. Электронная техника. Москва,

АСАДЕМ!А, 2005.

6. Трофимова Т.И., Курс физики. Москва, Высшая школа, 2003