36

Министерство образования Российской федерации

Южно-Российский государственный технический университет

(Новочеркасский политехнический институт)

Волгодонский институт юргту

Индивидуальные задания по

Линейной и векторной алгебре, аналитической геометрии

Новочеркасск

2003

УДК 514.742 (076.5)

Рецензент: д-р техн. наук, проф. Ю.С.Сысоев

Составители: Гладун К.К., Благина Л.В, Батаков А.И,.Лисичкина О.М,

Филиппова И.Н., Афиногенова М.А.

Индивидуальные задания по линейной и векторной алгебре, аналитической

геометрии /Волгодонский ин-т ЮРГТУ (НПИ).- Новочеркасск: ЮРГТУ, 2003. 32 с.

В сборнике представлены тридцать вариантов задач по линейной и векторной алгебре, аналитической геометрии, предназначенных для выполнения индивидуальных домашних заданий студентами всех специальностей института дневной формы обучения.

 Волгодонский ин-т ЮРГТУ, 2003.

 Коллектив авторов, 2003

Предисловие

Основу образовательного процесса студентов института составляет их самостоятельная работа. Для эффективной ее организации в учебные планы включено выполнение индивидуальных домашних заданий (ИДЗ).

Настоящий сборник содержит зачетные домашние задания по линейной , векторной алгебре и аналитической геометрии.

Каждая задача представлена тридцатью вариантами. Зачетные домашние задания выполняются по мере продвижения в изучении курса.

Прежде чем приступить к выполнению ИДЗ, необходимо ознакомиться с основными теоретическими положениями, а также изучить методы решения типовых задач, изложенных в методических указаниях прилагаемых к этому сборнику.

Решение задач студенты представляют в письменной форме с подробным его изложением. Нумерация задач в отчетной работе должна совпадать с нумерацией в расчетном задании. Титульная страница оформляется в соответствии с требованиями, предъявляемыми к оформлению курсовых работ.

В сроки, определенные учебным графиком, осуществляется защита ИДЗ в письменной форме или путем собеседования (по усмотрению преподавателя). Неверно решенные примеры возвращаются на доработку с указанием характера ошибки.

Во время защиты студент должен знать содержание основных теоретических положений, используемых при выполнении работы, а также уметь решать аналогичные примеры.

Повторная защита для студентов, не защитивших ИДЗ, назначается не позже, чем через неделю.

Зачетное домашнее задание №1

Матрицы, определители, системы линейных уравнений

1. Даны матрицы a, b, c, числа α и β.

Вычислить: а) C^.B; б) Α^.α + β^.B; в) А²+В²; г) А^-1.

1.1. ; ; α =2; β=3;

1.2. 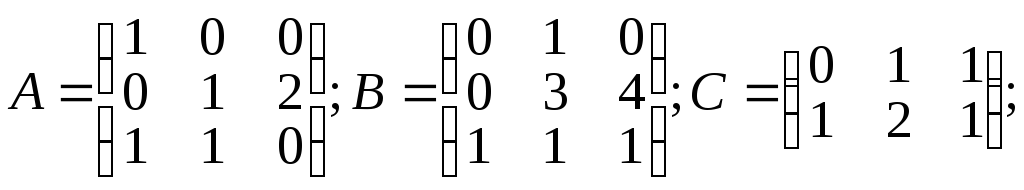α =3; β=3;

1.3. 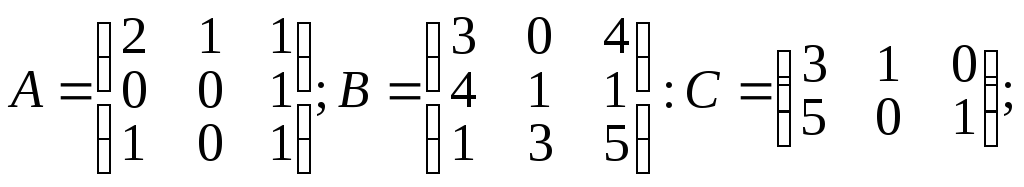α =4; β=1,5;

1.4. 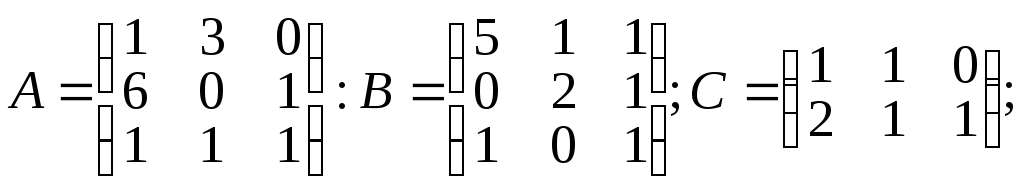α =2; β=2;

1.5. α =3; β=5;

1.6. α =4; β=6;

1.7. α =8; β=2;

1.8. α =2; β=3;

1.9. 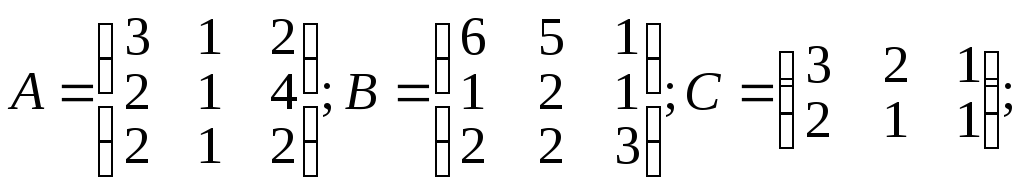α =3; β=7;

1.10. 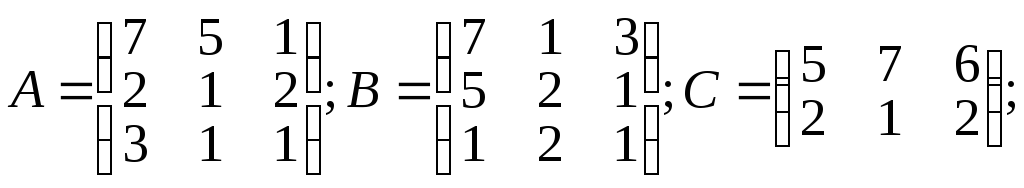α =5; β=10;

1.11. 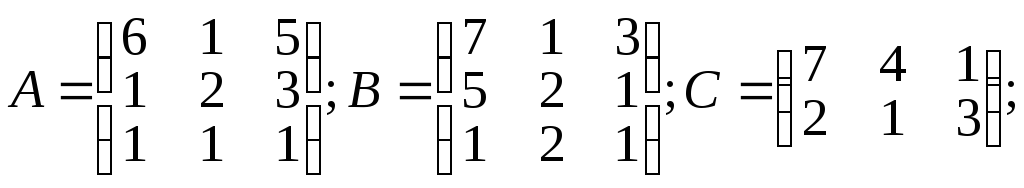α =2; β=8;

1.12. α =5; β=2;

1.13. α =4; β=6;

1.14. α =9; β=8;

1.15. 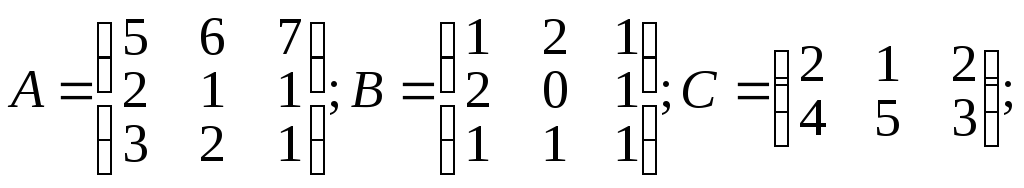α =6; β=2;

1.16. = 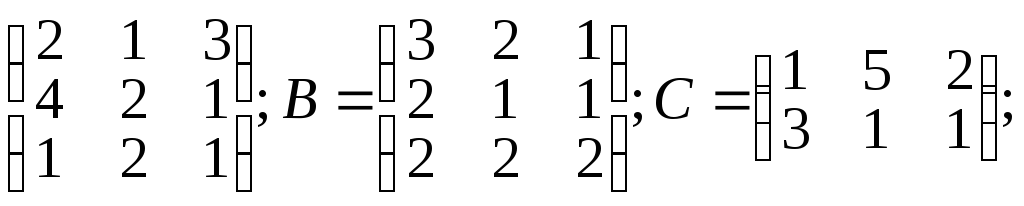α =4; β=3;

1.17. 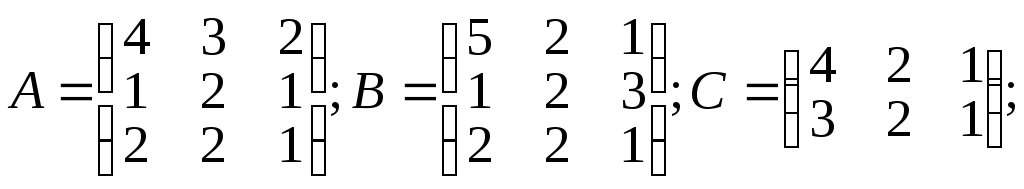α =3; β=9;

1.18. 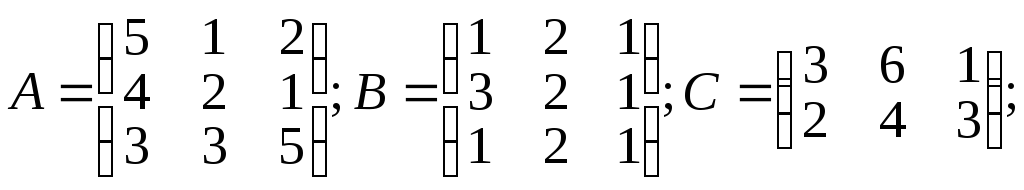α =2; β=5;

1.19. 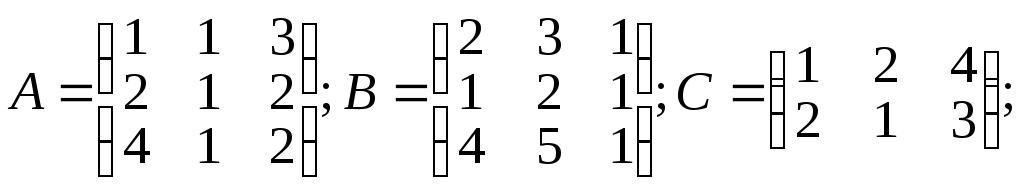α =5; β=5;

1.20. α =3; β=2;

1.21. 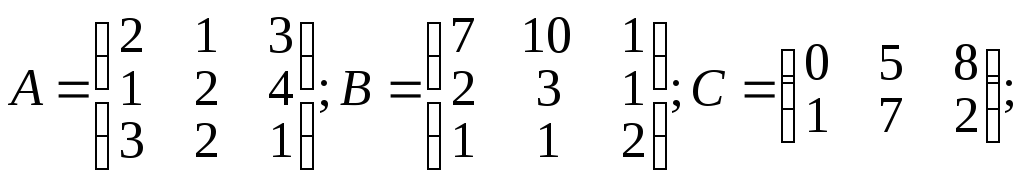α =7; β=4;

1.22. = α =5; β=4;

1.23. 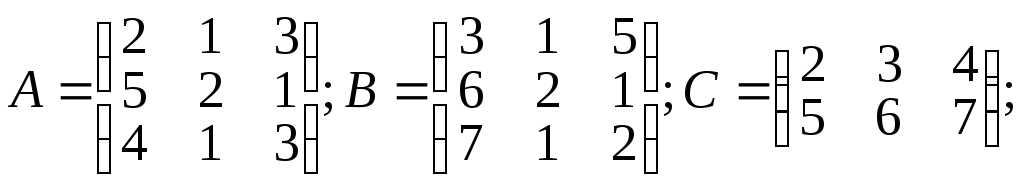α =2; β=3;

1.24. α =2; β=3;

1.25. α =6; β=2;

1.26. 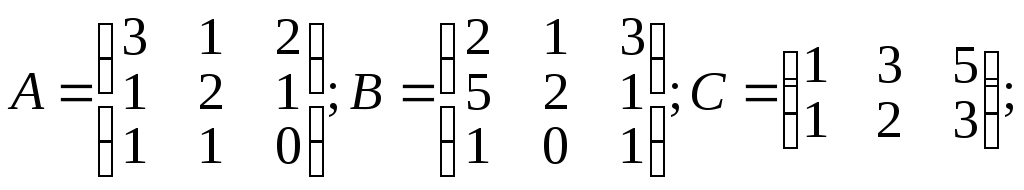α =3; β=4;

1.27. α =7; β=2;

1.28. 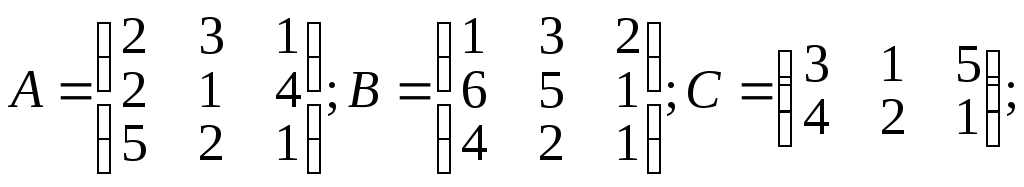α =3; β=4;

1.29. α =5; β=10;

1.30. 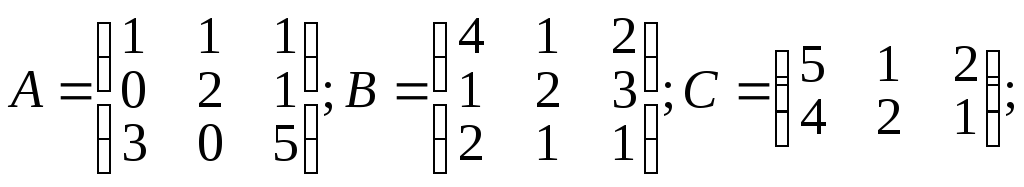α =4; β=2;