Задачи для подготовки к защите ргр № 1 «Элементы линейной алгебры»

№1. Выполните действия:

1) , где Е ― единичная матрица соответствующей размерности.

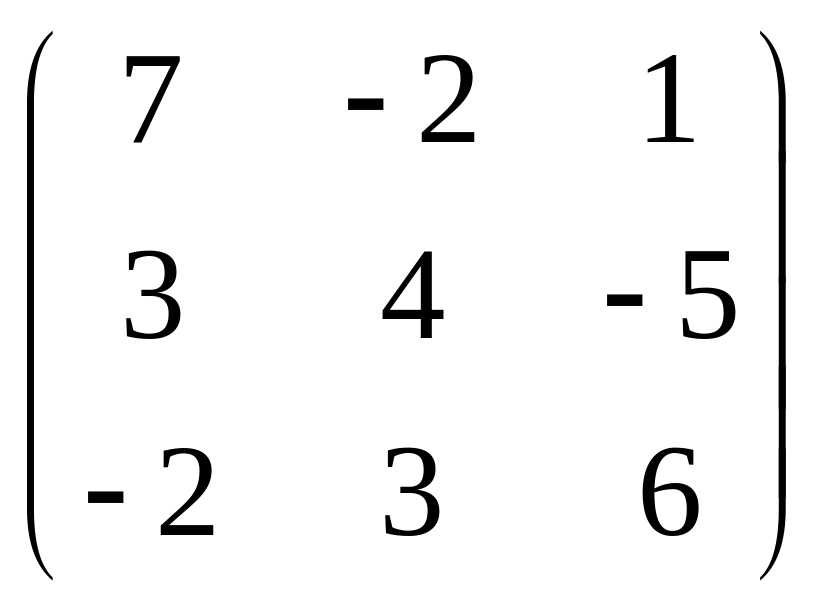2) , где А= , В=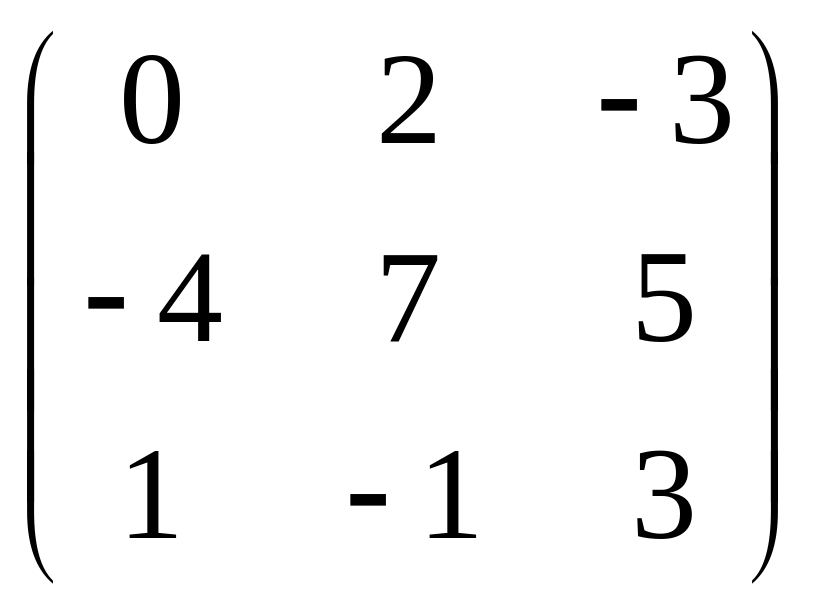 , Е ― единичная матрица.

№2. Решите систему линейных уравнений

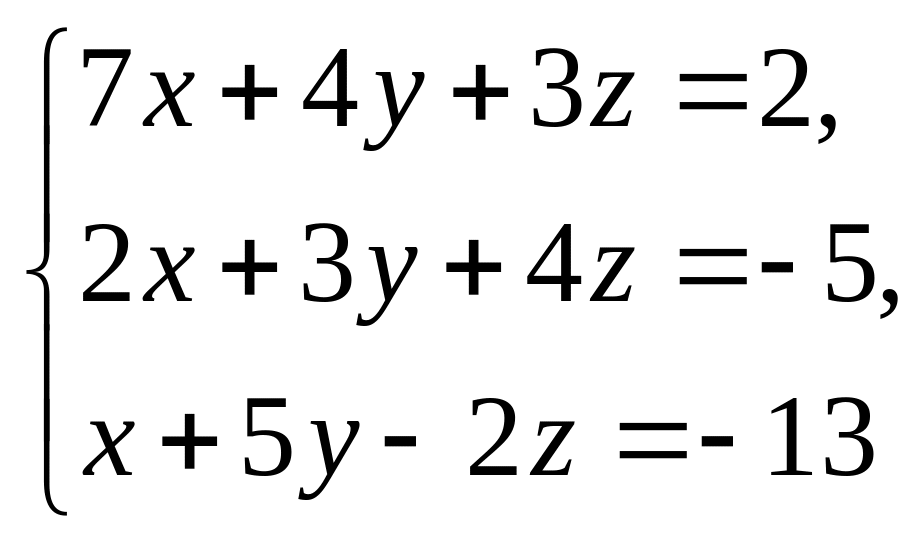
1) по правилу Крамера;

2) с помощью обратной матрицы;

3) методом Гаусса.

6. Образец ргр № 2 «Элементы векторной алгебры»

Используйте параметры: n=2, m=3, l=4.

№1. Дано: , Найти: а) , если ;

, b) , если .

,

.

№2. Дано: ,

,

.

Найти длину и направляющие косинусы вектора .

№3. Дано: А ( m, , 0), Найти: a) cos ABC;

B ( , 3, , b)

C ( , 1, 3), c) площадь треугольника АВС;

D (0, , 2). d) объем пирамиды АВСD.

Теоретические вопросы для подготовки к защите ргр № 2 «Элементы векторной алгебры»

1. Определение координат вектора, их геометрический смысл. Нахождение координат вектора по координатам его начала и конца.

2. Нахождение модуля вектора и направляющих косинусов вектора по его координатам.

3. Линейные операции над векторами в геометрической и координатной формах.

4. Определение и свойства скалярного произведения векторов. Условие перпендикулярности двух векторов.

5. Нахождение скалярного произведения векторов через их координаты.

6. Применение скалярного произведения для нахождения: a) угла между векторами; b) проекции вектора на вектор.

7. Определение и свойства векторного произведения векторов.

8. Определение коллинеарных векторов. Условие коллинеарности векторов.

9. Нахождение векторного произведения векторов через их координаты.

10. Применение векторного произведения векторов для: a) установления коллинеарности векторов; b) вычисления площадей параллелограмма и треугольника.

11. Определение и свойства смешанного произведения векторов.

12. Определение компланарных векторов. Условие компланарности векторов.

13. Нахождение смешанного произведения векторов через их координаты.

14. Применение смешанного произведения для: a) установления компланарности векторов; b) вычисления объемов.

Задачи для подготовки к защите ргр № 2 «Элементы векторной алгебры»

№1. Даны векторы и . Найдите координаты вектора .

№2. Найдите координаты и длину вектора если

№3. Найдите скалярное произведение векторов и если длина вектора равна 5, длина вектора равна 4, а угол между векторами и равен

№4. Найдите скалярное произведение векторов и , если

№5. Найдите косинус угла между векторами и , если

№6. Найдите значение при котором векторы и перпендикулярны.

№7. Найдите векторное произведение векторов и .

№8. Найдите площадь параллелограмма, построенного на векторах и

№9. Найдите площадь треугольника АВС, если

№10. Найдите значения и , при которых векторы и коллинеарны.

№11. Найдите смешанное произведение векторов

№12. Найдите объем пирамиды если

№13. Выясните, лежат ли точки , , , в одной плоскости.