Самостоятельная работа «Решение системы линейных уравнений»

Дана система линейных уравнений:

2х₁+3х₂+7х₃+6х₄=1

3х₁+5х₂+3х₃+х₄=3

5х₁+3х₂+х₃+3х₄=4

3х₁+3х₂+х₃+6х₄=5

Пусть матрица записана в ячейки А10:D13, а свободные члены - в ячейки F10:F13.

В Excel имеются следующие функции для работы с матрицами:

МОБР – обращение матрицы,

МОПРЕД – вычисление определителя матрицы,

МУМНОЖ – матричное произведение двух матриц,

ТРАНСП – транспонирование матрицы.

Решение линейной системы АХ=В, где А - матрица коэффициентов, В - столбец (вектор) свободных членов, Х - столбец (вектор) неизвестных, имеет вид Х=А^-1В, где А^-1 - обратная матрица.

Выделите под вектор решений диапазон G10:G13 и введите формулу: =МУМНОЖ(МОБР(А10:D13); F10:F13)

Для получения решения нажмите Ctrl+Shift+Enter; сделайте проверку решения: в первое уравнения подставьте значения корней.

Самостоятельная работа «Построение уравнения линейной регрессии»

i	xi	yi
1	1	7
2	2	9
3	3	12
4	4	13
5	5	14
6	6	17

Имеются две наблюдаемые величины x и y, например, объем реализации фирмы, торгующей автомобилями, за шесть недель ее работы. Значения наблюдаемых величин приведены в таблице, где x – отчетная неделя, а y – объем реализации за эту неделю.

Необходимо построить линейную модель y=аx+b, которая бы наилучшим образом описывала наблюдаемые значения. Такая модель называется уравнением регрессии. Для его построения определяют коэффициенты а и b так, чтобы минимизировалась некоторая целевая функция. В качестве такой функции обычно выбирают сумму квадратов отклонений заданных значений y_i от соответствующих значений, вычисляемых с помощью уравнения регрессии. Для решения этой задачи в ячейки D3:E3 вводим ориентировочные значения коэффициентов a, b (например, a=2, b=2), а в ячейку F3 (Рис. 4.19) вводим целевую функцию СУММКВРАЗН(C2:C7;E3+D3*B2:B7).

Р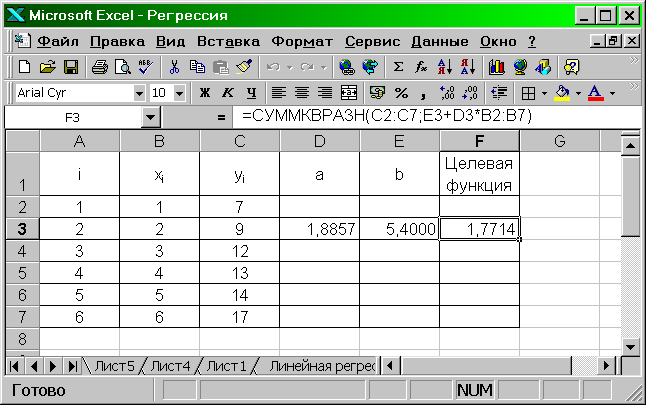 ис. 4.19. Вычисление коэффициентов уравнения регрессии с использованием целевой функции

В ыбираем команду Сервис/Поиск решения и заполняем диалоговое окно Поиск решения (Рис. 4.20).

Рис.4.20. Диалоговое окно Поиск решения

Результат нахождения параметров a и b – на рис. 4.20. Полученное уравнение регрессии: y = 1,8857x + 5,4.

Другой способ получения уравнения линейной регрессии основывается на построении линии тренда. Построим точечный график по диапазону ячеек B2:C7, выделим точки графика двойным щелчком, а затем щелкнем правой кнопкой мыши. В появившемся контекстном меню выберем команду Линии тренда. Выберем Тип/Линейная, а на вкладке Параметры установим флажки: Поместить уравнение на диаграмме, Поместить на диаграмму величину достоверности аппроксимации (R²). На рис. 4.21 – результат построения линии тренда. Коэффициент R² характеризует ту долю дисперсии (изменений) функции y, которая прогнозируется с помощью найденного уравнения регрессии. Этот коэффициент называют ещё коэффициентом детерминации. По его величине судят о том, можно ли использовать уравнение регрессии для прогнозирования.

Р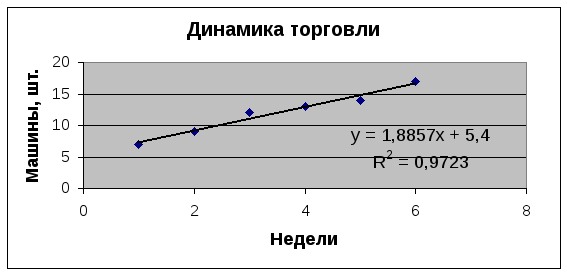 ис. 4.21. Построение линии тренда

Для прогноза с помощью уравнения регрессии используется встроенная функция ТЕНДЕНЦИЯ(<известные y>;<известные x>;<новые x>), которая вычисляет ожидаемые новые значения y для новых x, если известны некоторые опытные значения x и y. Вычисления делаются в предположении, что x и y зависят линейно. Вычислите ожидаемый объем реализации автомобилей за 7-ю, 8-ю и 9-ю недели работы фирмы.

В рассматриваемой задаче объем реализации автомобилей (y) был дан за 6 недель (x= 1,2,...,6). Так как результат должен выводиться в три ячейки, значит функция ТЕНДЕНЦИЯ() должна вводиться как функция обработки массива. Выделяется диапазон ячеек C8:C10 (Рис. 4.22), вводится функция ТЕНДЕНЦИЯ() и нажимаются клавиши Ctrl+Shift+Enter (вместо обычного Enter). Результат прогноза виден на рис. 4.22.

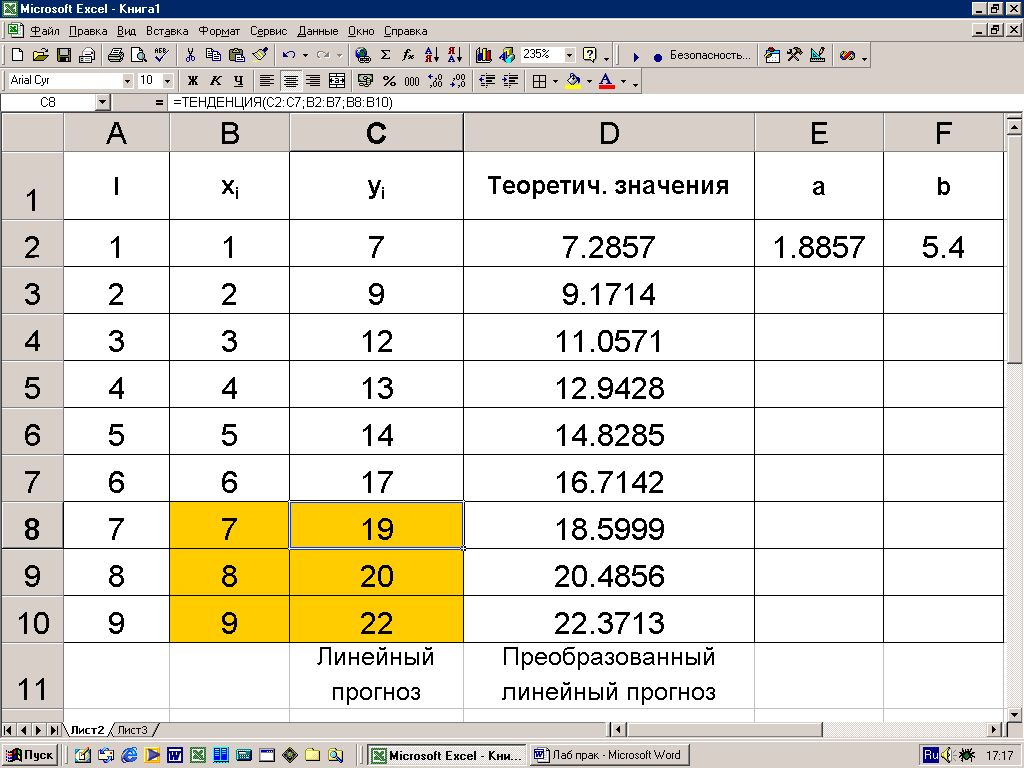
Рис.4.22. Вычисление прогнозных значений y с использованием функции ТЕНДЕНЦИЯ

Таким образом, на 7-й неделе работы фирмы ожидается продажа 19-ти машин, на 8-й неделе – продажа 20-ти машин, на 9-й неделе – продажа 22-х машин. При этом надо иметь в виду, что математический прогноз подтвердится только в том случае, если наметившаяся за первые шесть недель тенденция увеличения продаж сохранится ещё в течение трёх недель. Таким образом, математический прогноз может быть успешным только в рамках принятой модели. При изменении ситуации необходимо изменять модель, например, вместо линейного уравнения регрессии использовать параболическое или экспоненциальное.