Самостоятельная работа «Построение графика функции с условиями»

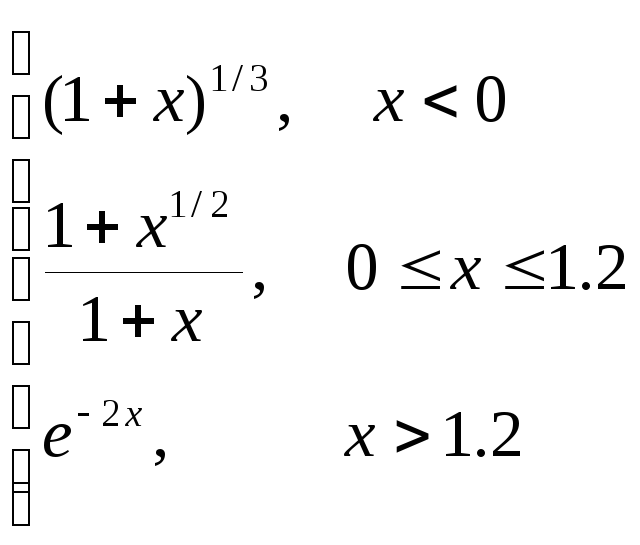
Y=

при x  [-3, 3]

Для построения графика функции необходимо сначала построить таблицу ее значений при различных значениях аргумента, причем обычно аргумент изменяется с фиксированным шагом. Шаг выбирают небольшим, чтобы таблица значений функций отражала их поведение на интервале табуляции. В нашем случае будем считать, что шаг изменения аргумента равен 0,2. Необходимо найти: y(-3), y(-2,8), y(-2,6), …, y(3). С этой целью в диапазон ячеек А2:А32 введём автозаполнением следующие значения переменной х: -3; -2,8; -2,6; …; 3. В ячейки A1 и B1 введём заголовки столбцов: x и y.

В ячейку В2 вводится формула:

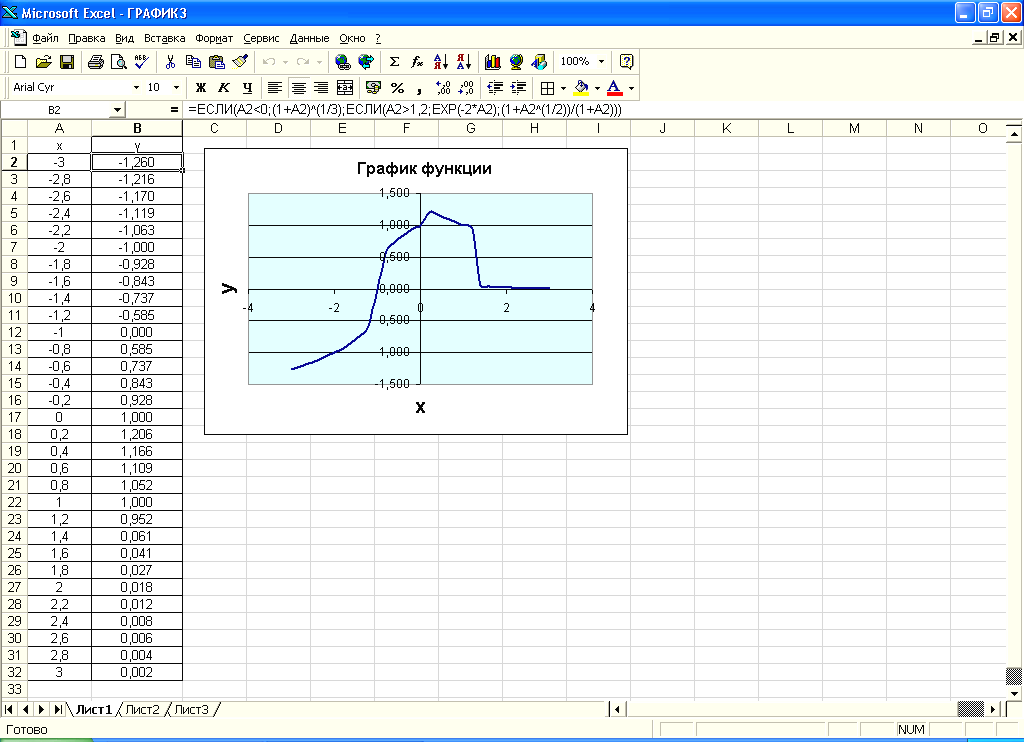= ЕСЛИ(А2<0;(1+A2)^(1/3);ЕСЛИ(A2>1,2;EXP(-2*A2);(1+A2^(1/2))/(1+A2)))

Рис. 4.13. График функции с двумя условиями

Самостоятельная работа « Построение двух графиков в одной системе координат»

Построить в одной системе координат графики следующих двух функций:

y = 2sin(x) и z = 3cos(2x) – sin(x) при x  [-3;3]

В ячейки A2:A17 вводим значения переменной x от –3 до 3 с шагом 0,2. В ячейки B1 и C1 вводим y и z соответственно, а в ячейки B2 и C2 – формулы:

= 2*sin(A2)

=3*cos(2*A2) – sin(A2)

Выделим диапазон B2:C2, установим указатель мыши в его правом нижнем углу и с помощью автозаполнения скопируем формулы в ячейки B3:C32.

В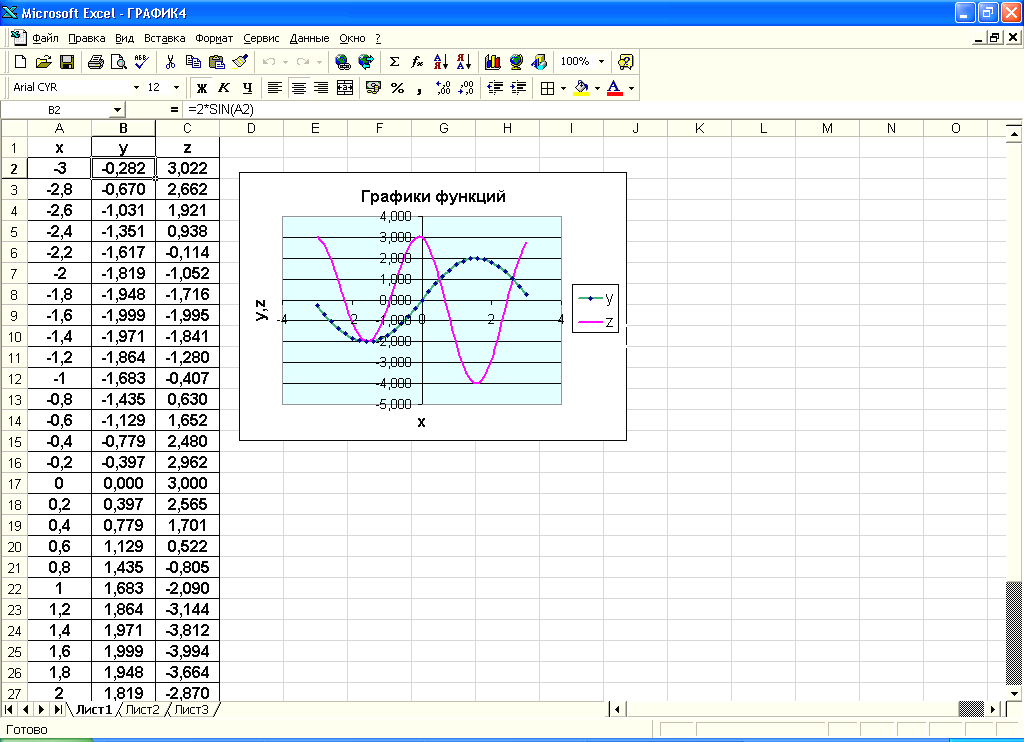 ыделим диапазон ячеек A1:C32, вызовем Мастер диаграмм. Выберем тип диаграммы – Точечная и вид графика. На втором шаге Мастера диаграмм в группе Ряды данных установим переключатель в положение В столбцах. На третьем шаге Мастера диаграмм в поле Название диаграммы вводим Графики функций, в поле Ось x – x, в поле Ось y – y и z. Нажатие кнопки Готово завершает построение графиков (Рис.4.14).

Рис. 4.14. График двух функций в одной системе координат

Графики функций y и z могут для наглядности различаться по типу линий. Для этого график, внешний вид которого мы хотим изменить, выделяется и с помощью Контекстного меню вызывается диалоговое окно Форматирование элемента данных, которое позволяет изменять тип, толщину и цвет линии, а также тип, цвет и фон маркера.

Самостоятельная работа «Нахождение корней уравнения»

Найти все корни уравнения

x³ – 0.01x² – 0.7044x + 0.1391 = 0

У полинома третьей степени имеется не более трех вещественных корней. Для нахождения корней их предварительно нужно локализовать, т.е. определить интервалы, на которых они расположены. С этой целью построим график функции

y = x³ – 0.01x² – 0.7044x + 0.1391

н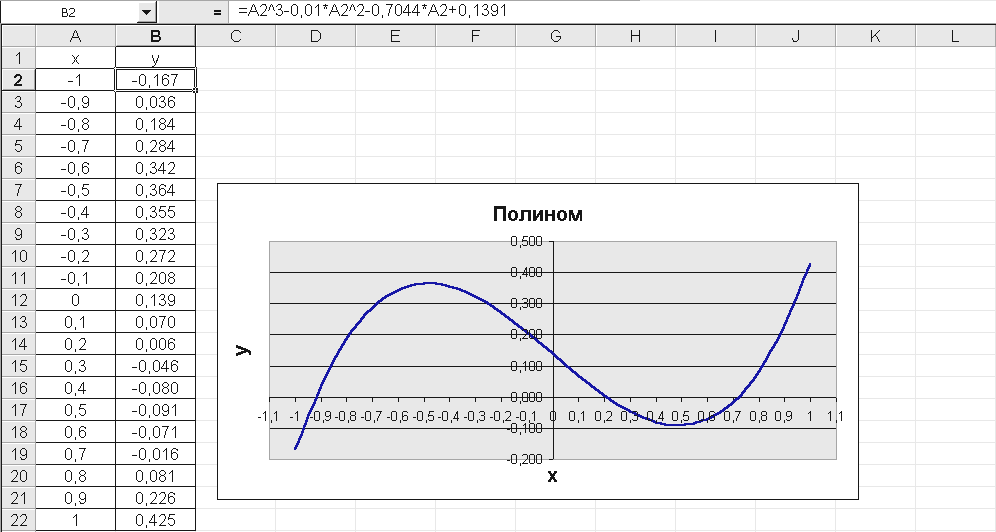 а отрезке [-1,1] с шагом 0.1. В столбец А введем значения x, в столбец В – значения y, вычисленные по формуле (рис. 4.15):

= A2^3 – 0.01*A2^2 – 0.7044*A2 + 0.1391

Рис. 4.15. Локализация корней полинома

И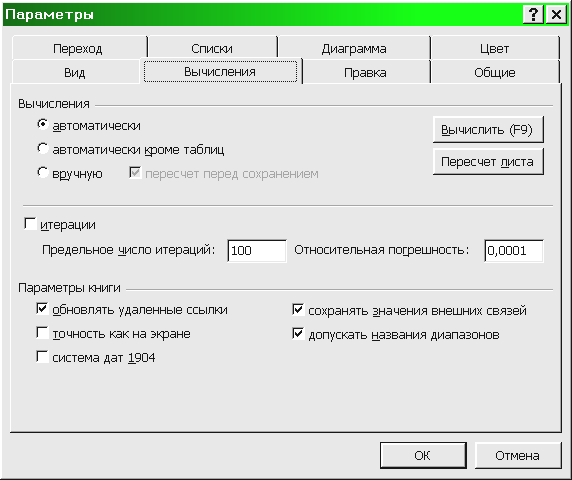 з рисунка видно, что полином меняет знак на интервалах: [-1, -0.8], [0.2, 0.3], [0.7, 0.8]. Это значит, что на каждом из них имеется корень данного уравнения. Поскольку полином третьей степени имеет не более трех действительных корней, мы локализовали все его корни. Найдем их методом последовательных приближений с помощью команды Сервис/ Подбор параметра. Но, прежде всего, зададим относительную погрешность и предельное число итераций равными, например, 0.0001 и 1000. Эти параметры Excel задаются с помощью команды Сервис/ Параметры – на вкладке Вычисления (рис. 4.16).

Рис.4.16. Вкладка Вычисления диалогового окна Параметры

В качестве начальных приближений можно взять любые точки из отрезков локализации корней, например, точки: -0.95, 0.25 и 0.75. Введем их в диапазон ячеек С2:С4. В ячейку D2 введем формулу:

= C2^3 – 0.01*C2^2 – 0.7044*C2 +0.1391

Выделим эту ячейку и, с помощью маркера заполнения распространим введенную в нее формулу на диапазон D2:D4. Таким образом, в ячейках D2:D4 вычисляются значения полинома при значениях аргумента, введенного в ячейки C2:C4 соответственно. Теперь выберем команду Сервис/Подбор параметра и заполним диалоговое окно Подбора параметра (рис. 4.17) следующим образом.

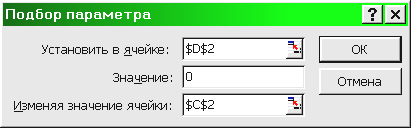
Рис. 4.17. Диалоговое окно Подбор параметра

В поле Установить в ячейке введем D2. Отметим, что в этом поле дается ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения. Для нахождения корня уравнения с помощью подбора значения параметра, надо записать уравнение так, чтобы его правая часть не содержала переменную.

В поле Значение введем 0 (в этом поле указывается правая часть уравнения). В поле Изменяя значение ячейки введем С2 (в этом поле дается ссылка на ячейку, отведенную под переменную). Вводить ссылки на ячейки в поля диалогового окна Подбор параметра удобнее не с клавиатуры, а щелчком на соответствующей ячейке. При этом Excel автоматически будет превращать их в абсолютные ссылки (в нашем примере $D$2, $C$2).

П осле нажатия кнопки OK процедура подбора параметров находит приближенное значение корня, которое помещает в ячейку С2. В данном случае оно равно -0.920. Как выглядит диалоговое окно Результат подбора параметра после завершения поиска решения, показано на рис. 4.18.

Рис. 4.18. Диалоговое окно Результат подбора параметра

Аналогично в ячейках С3 и С4 находим два оставшихся корня. Они равны 0.210 и 0.720.