7. Формулы Крамера

Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А

Δ = det (a_{i j})

и n вспомогательных определителей Δ_i (i=), которые получаются из определителя Δ заменой i-го столбца столбцом свободных членов.

Формулы Крамера имеют вид:

( i  = ). (7.1)

Из (7.1) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3):

если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:

Если главный определитель системы Δ и все вспомогательные определители Δ_i = 0 (i= ), то система имеет бесчисленное множество решений.

Если главный определитель системы Δ = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.

7.1. Пример 7.1

Решить методом Крамера систему уравнений:

x₁ +   x₂ +  x₃ +      x₄ = 5,

x₁ + 2x₂ -   x₃ +    4x₄ = -2,

2x₁ -  3x₂ -   x₃ -     5x₄ = -2,

3x₁ +   x₂ +2x₃ + 11 x₄ = 0.

Решение. Главный определитель этой системы

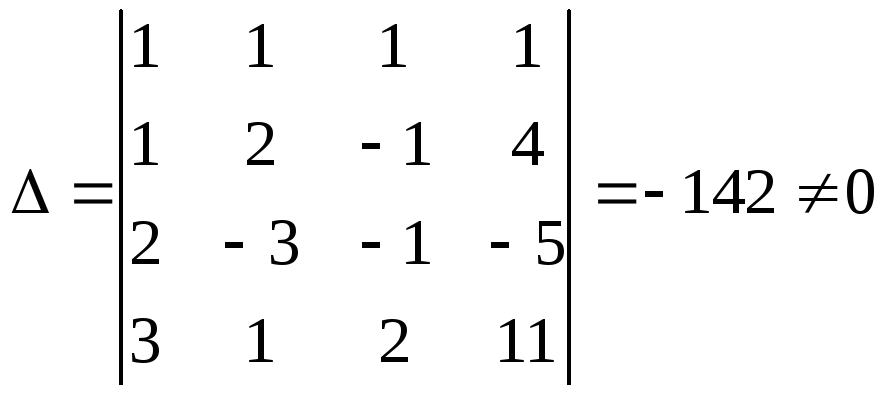
значит, система имеет единственное решение. Вычислим вспомогательные определители Δ_i ( i = ), получающиеся из

Для заметок

определителя Δ путем замены в нем столбца, состоящего из коэффициентов при x_i, столбцом из свободных членов:

 

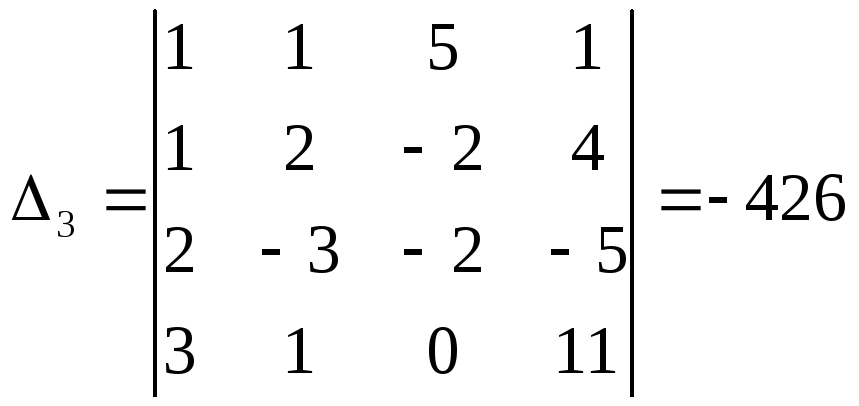
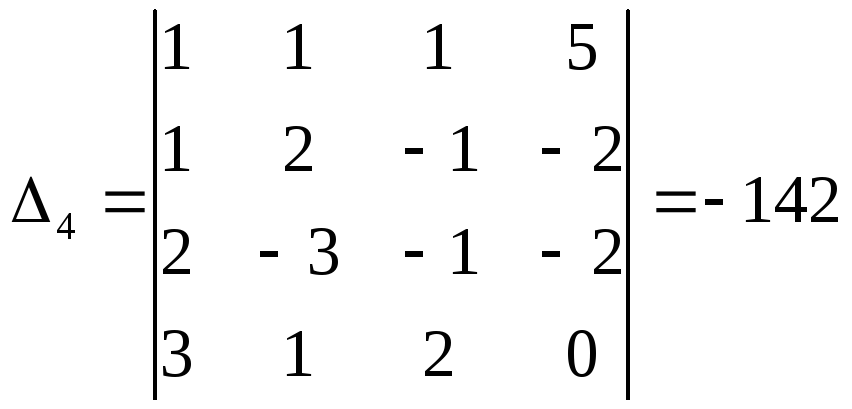
Отсюда , , ,

решение системы - вектор С=(1, 2, 3, -1)^T.

8. Метод Гаусса

Метод Гаусса является наиболее распространенным точным методом исследования и решения систем линейного уравнения (как квадратных, так и не квадратных). Основная идея его состоит в том, что посредством элементарных преобразований система приводится к равносильной системе треугольного или трапециидального (ступенчатого) вида, по которому легко видеть какая система: совместно или несовместна, определенная или неопределенная. При этом, если система совместна, то все решения определяются непосредственно.

К элементарным преобразованиям систем относят следующие:

1. перестановка любых двух уравнений системы;

2. умножение любого уравнения системы на число не равное нулю;

3. вычеркивание уравнения, все коэффициенты которого равны нулю;

4. вычитание из любого уравнения системы любого другого, умноженного на отличное от нуля число;

5. переобозначение неизвестных.

Любое элементарное преобразование приводит к равносильной системе. Применение метода Гаусса состоит в поэтапном исключении неизвестных из уравнений.

Поясним метод Гаусса на конкретных примерах.

8.1. Пример 8.1

Исследовать систему

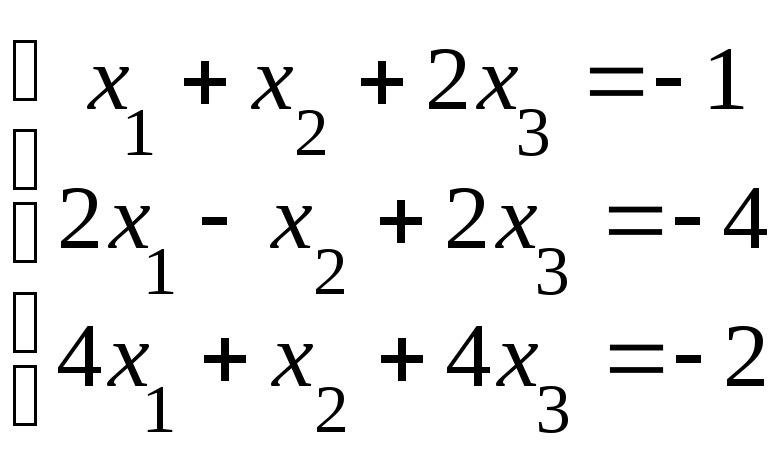(8.1)

Преобразуем систему (8.1), исключив из второго и третьего уравнений члены содержащие (добившись, чтобы коэффициенты перед были равны нулю).

1 шаг. Умножим обе части первого уравнения на коэффициент при , из второго уравнения, взятый с противоположным знаком, т.е. на -2:

, (8.2)

а обе части второго уравнения умножим на коэффициент при из первого уравнения, т.е. 1.

. (8.3)

Сложим почленно уравнения (8.2) и (8.3):

. (8.4)

2 шаг. Аналогичным образом поступим с третьим уравнением. Умножим обе части первого уравнения на коэффициент при третьего уравнения, взятый с противоположным знаком, т.е. на -4:

, (8.5)

а третье уравнение – на коэффициент при первого уравнения, т.е. на 1:

. (8.6)

Сложим почленно уравнения (8.5) и (8.6):

. (8.7)

Подставим в систему (8.1) вместо второго и третьего уравнений (8.4) и (8.7) соответственно. Система (8.1) примет вид:

. (8.8)

3 шаг. Затем преобразуем третье уравнение, исключив из него член, содержащий . Для этого обе части второго уравнения умножим на коэффициент при из третьего уравнения, взятый с противоположным знаком, т.е. на 3, получим

Для заметок

. (8.9)

Обе части третьего уравнения умножим на коэффициент при из второго уравнения, т.е. на -3:

. (8.10)

Сложим почленно уравнения (8.9) и (8.10):

. (8.11)

Заменим в системе (8.8) третье уравнение равносильным уравнением (8.11):

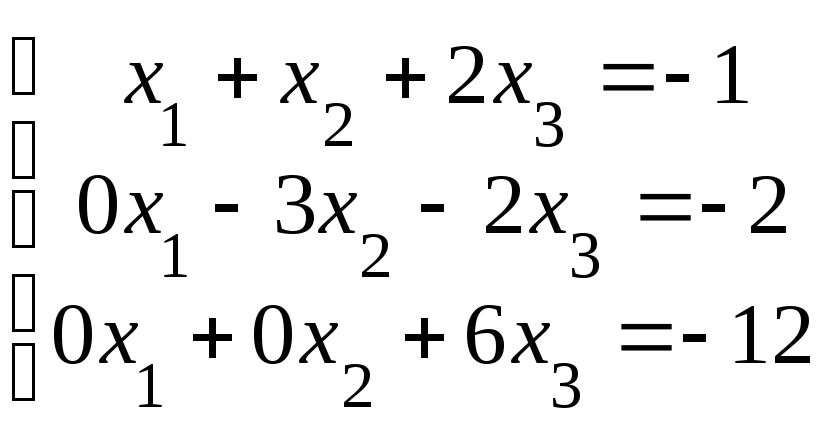. (8.12)

Таким образом, от исходной системы (8.1) мы перешли к равносильной системе (8.12), которая имеет треугольный вид (ступенчатый). Такое преобразование называют прямым ходом метода Гаусса.

4 шаг (обратный ход). Из последнего уравнения системы (8.2) найдем :

.

Используя второе уравнение и найденное значение , найдем :

, , .

Используя первое уравнение и найденное значение и , найдем :

, .

Таким образом, исходная система имеет единственное решение

.

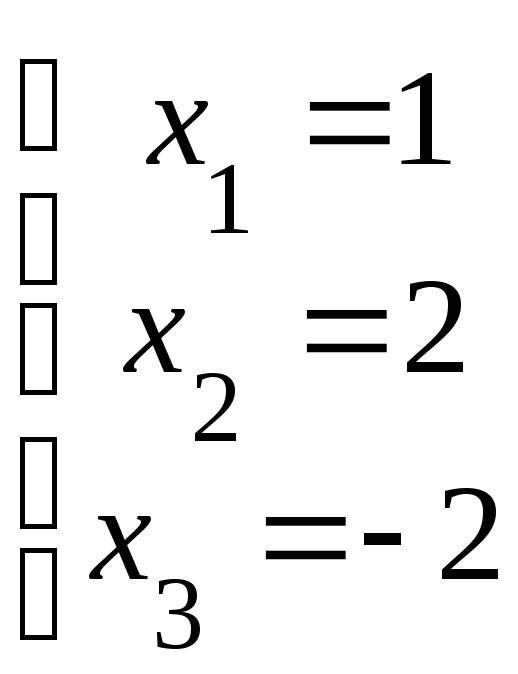Замечание. Предложенные преобразования систем можно формализовать. Можно выполнять операции не над системой, а на её аналоге – матрице. Построим расширенную матрицу вида

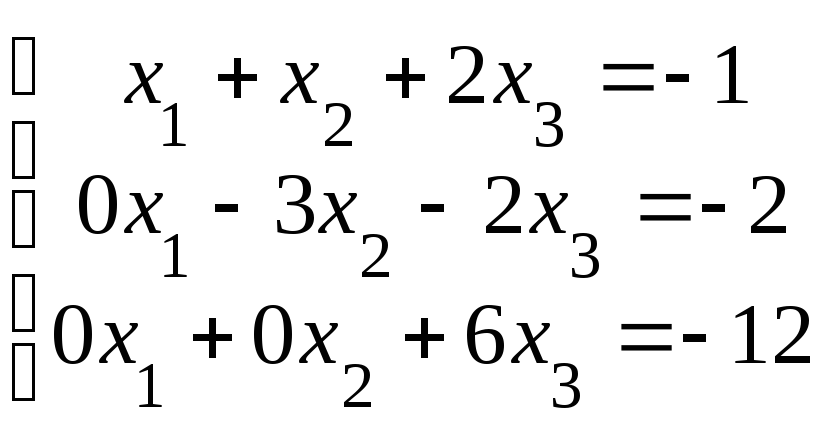
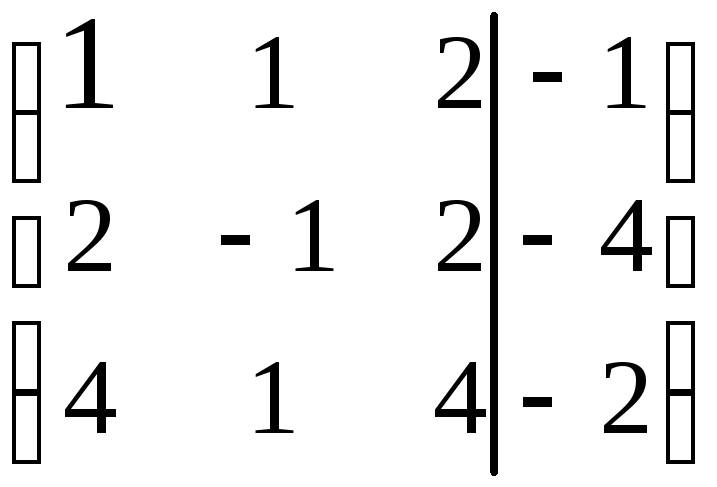(8.13)

Выберем в качестве разрешающей строки первую, а в качестве разрешающего элемента (в разрешающей строке это любой не нулевой элемент) выберем элемент (он выделен жирным шрифтом) и с помощью неё преобразуем вторую и третью строки так, чтобы в первом столбце под 1 получились нули. При этом можно использовать мнемоническое правило прямоугольников. Мысленно строится прямоугольник вида

Здесь точками обозначены произвольные элементы матрицы (в том числе и элементы, образованные свободными членами). Здесь элемент разрешающий элемент. Тогда на место элемента (выделен жирным шрифтом) ставится число равное

. (*)

Используя правило прямоугольников, преобразуем вторую и третью строки

.

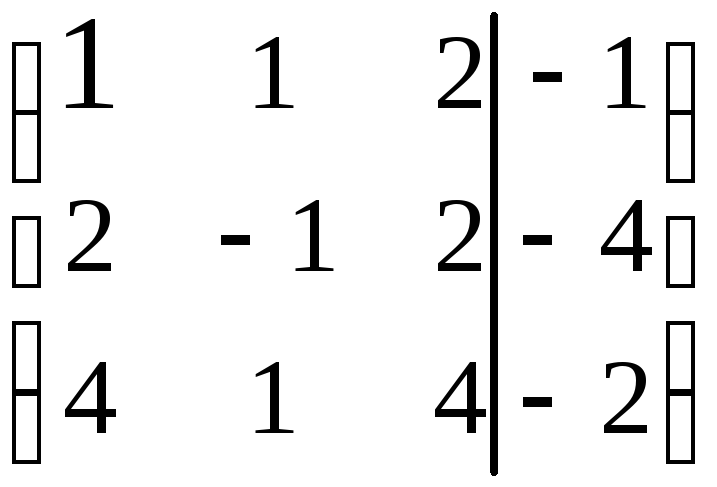
Затем выберем в качестве разрешающей строки вторую, а в качестве разрешающего элемента элемент (он выделен жирным шрифтом). Используя правило прямоугольников, преобразуем третью строку.

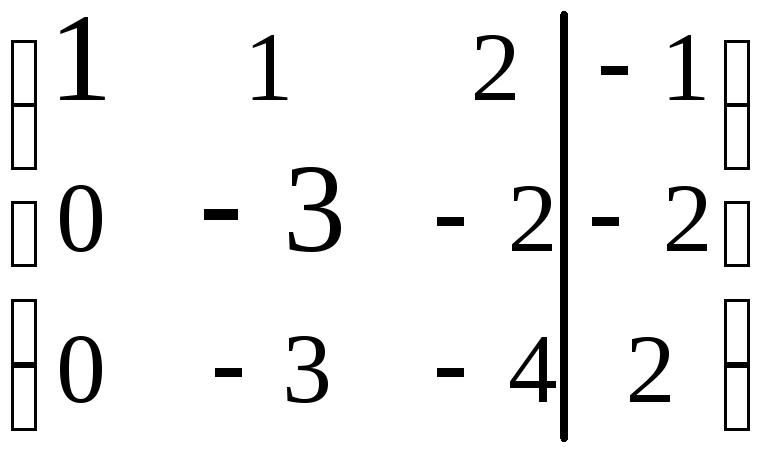
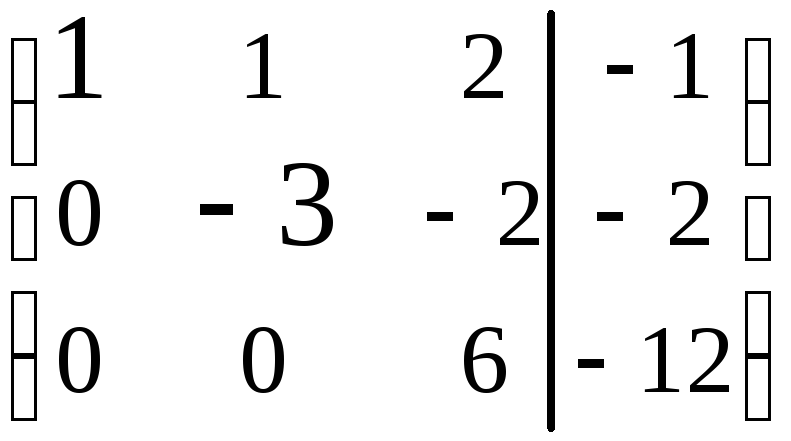
На этом заканчивается прямой ход метода Гаусса. Последняя матрица представляет собою символическую запись системы (8.12)

.

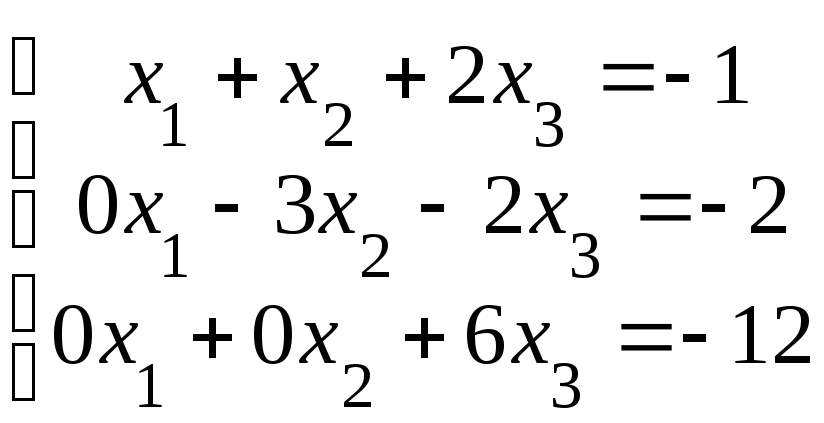Применяя обратный ход, также как это было сделано выше, получим решение системы

.

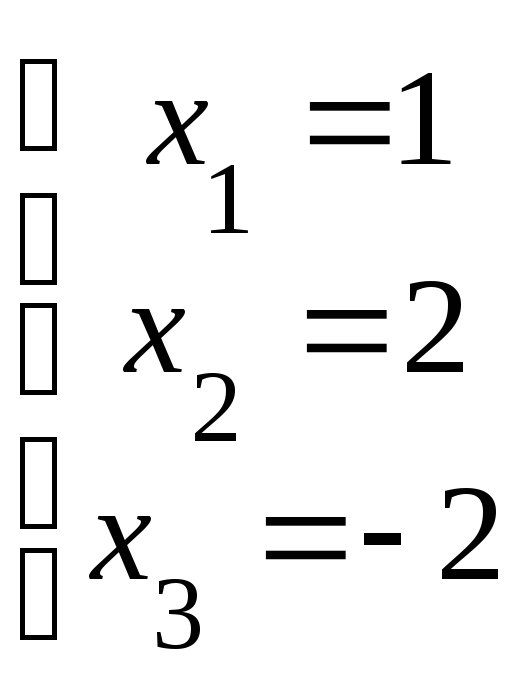Для заметок

8.2. Пример 8.2

Исследовать систему

(8.14)

Воспользуемся методом Гаусса.

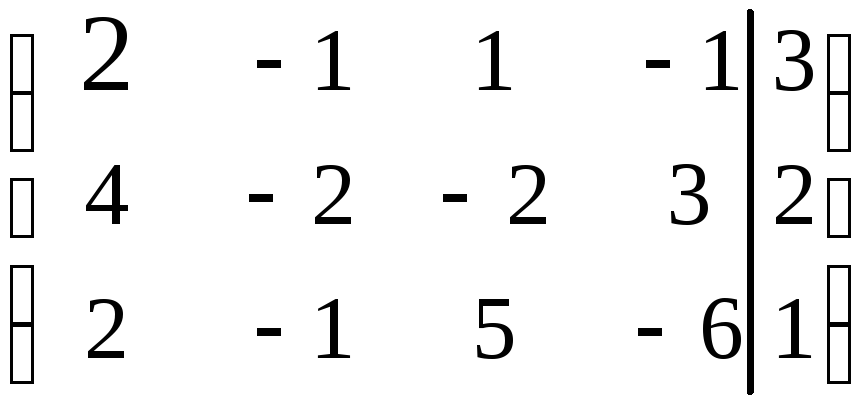
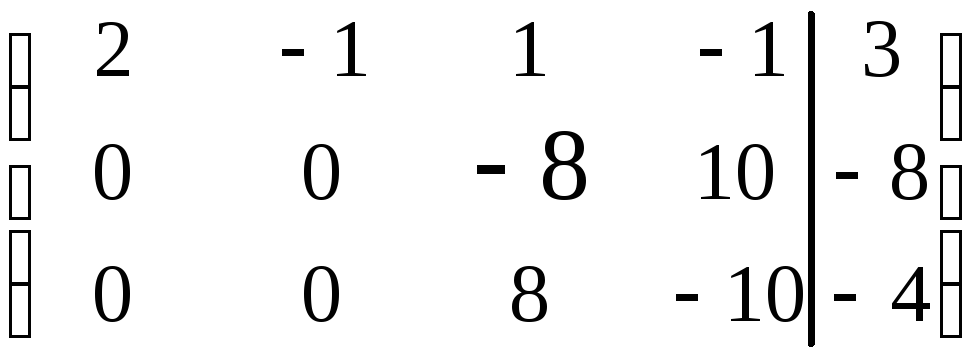
Поделив вторую строку на 2, а третью на 96, получим

.

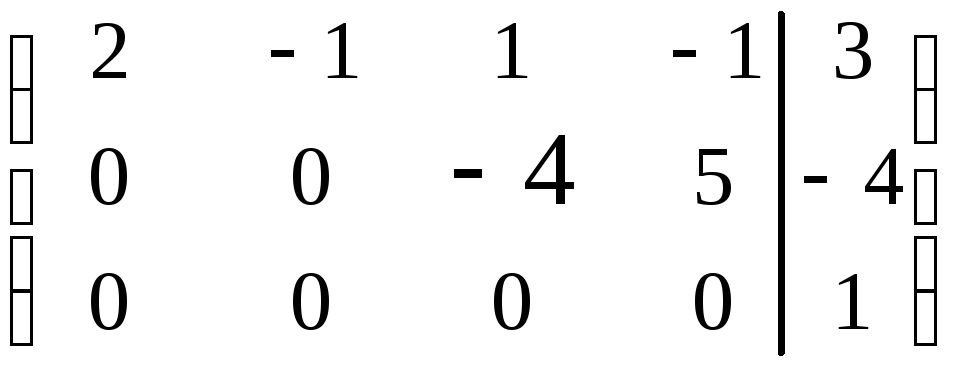
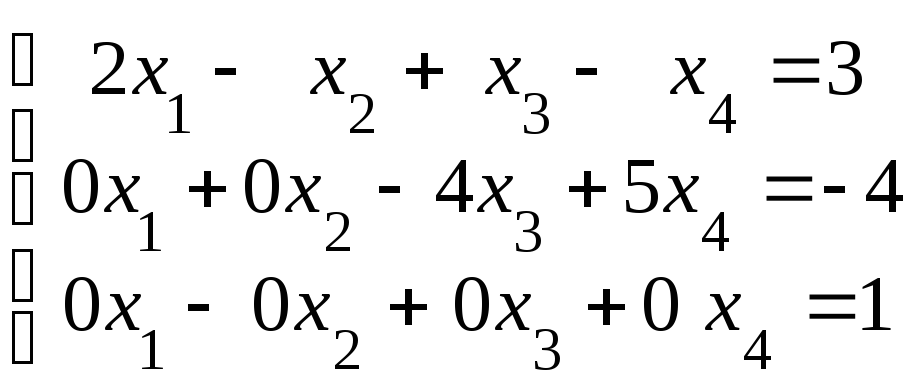Из последнего уравнения видно, что не существует такого значения , при котором оно будет верным равенством, т.к. левая

часть уравнения при любом значении равна 0, а правая всегда равна 1. Таким образом, можно сделать вывод, что исходная система несовместно.

8.3. Пример 8.3

Исследовать систему

(8.15)

Воспользуемся методом Гаусса.

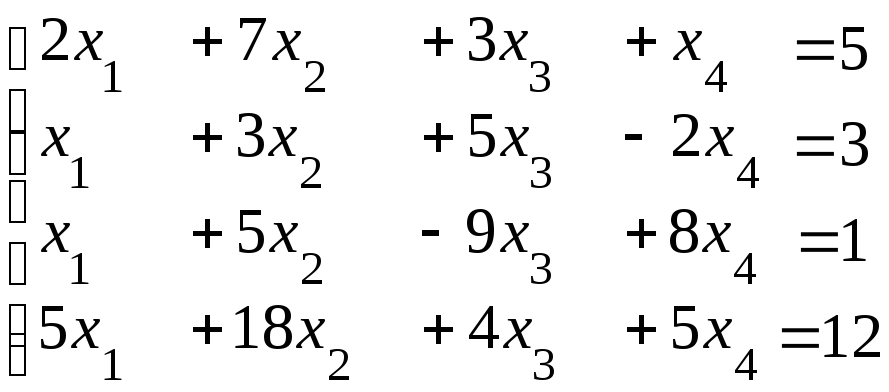
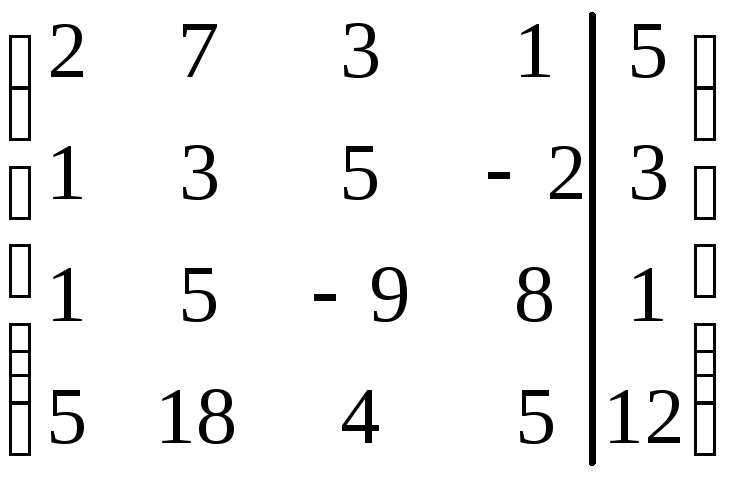
Поделим элементы третьей строки на 3. Получим

.

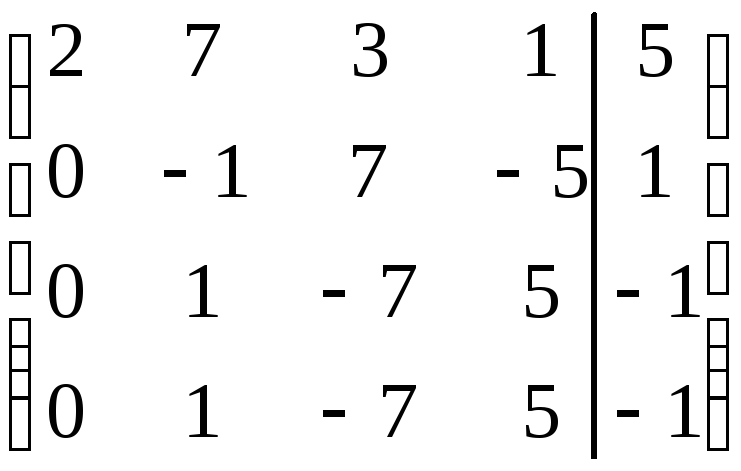Очевидно, второе, третье и четвертые уравнения совпадают, поэтому два последних уравнения можно исключить из матрицы (системы):

.

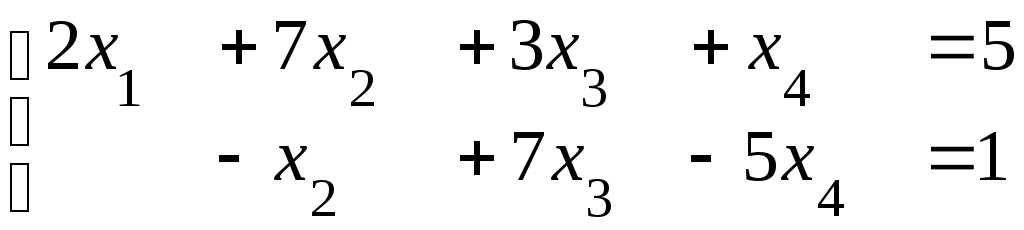Перенесем члены, содержащие неизвестные и в правые части (это свободные неизвестные, а и - базисные неизвестные). Система примет вид

.

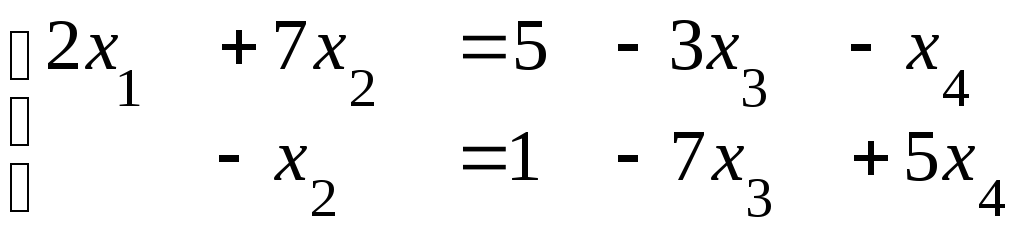Выразим и через свободные неизвестные и , которые могут принимать произвольные значения. Из второго уравнения

.

Используя это значение, из первого уравнения выразим через и .

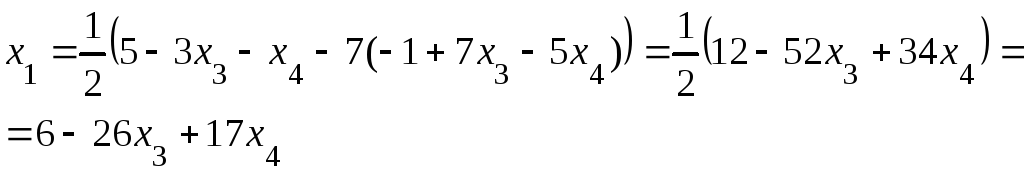
Таким образом, общее решение исходной системы имеет вид

.

Здесь С₁ и С₂ произвольные константы.

Напомни, что и называются базисными неизвестными.

Для заметок

Решение, полученное из общего при С₁ = С₂ =0 называют базисным решением. Если при этом базисные неизвестные неотрицательны, то такое решение называют опорным.