III. Понятие градиента
Пусть
функция двух переменных
имеет в области
частные производные
,
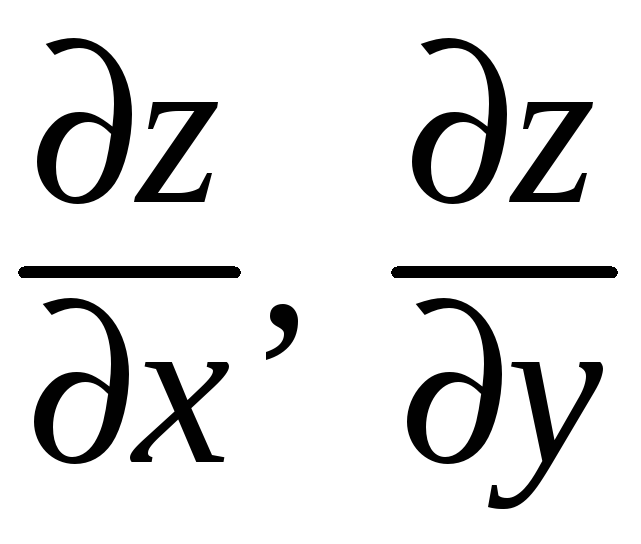и
.
Определение.
Градиентом
функции
в точке
называется вектор grad
,
координатами которого являются значения
частных производных в этой точке:
grad
.
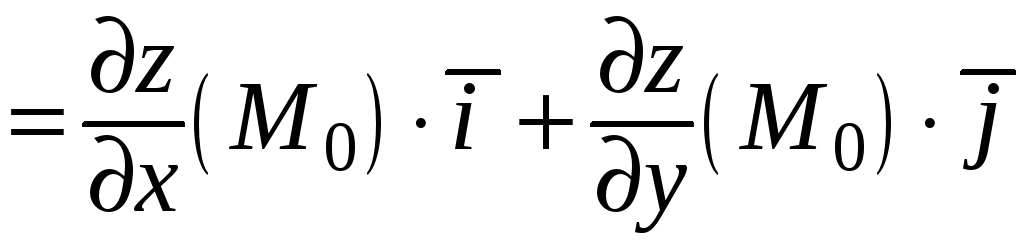Пример.
Пусть
.
Тогда
;
;
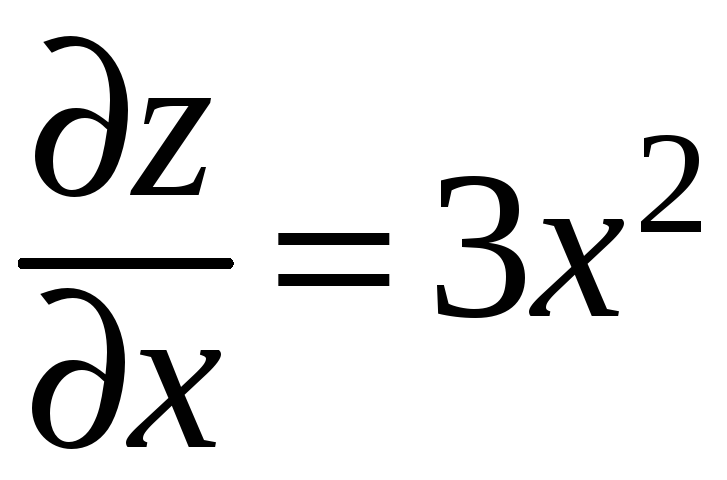grad
.
В
точке
:
grad
.
Аналогичным
образом определяется градиент в случае
функции большего числа переменных.
Например, для функции трех переменных
:
grad
.
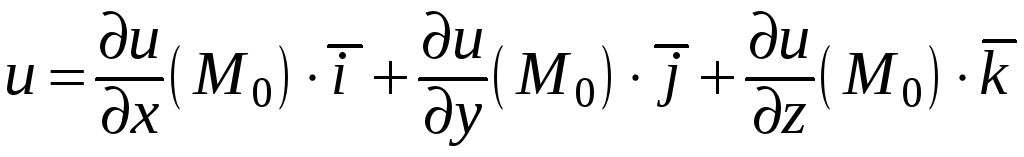(28)
IV. Связь производной по направлению с градиентом
Пусть
функция
имеет в
окрестности точки
частные производные
,
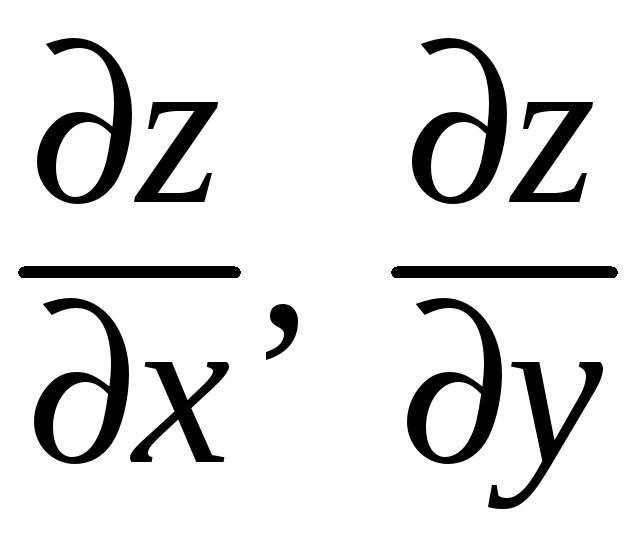и в самой точке
частные производные непрерывны, так
что справедлива
формула (24):
.
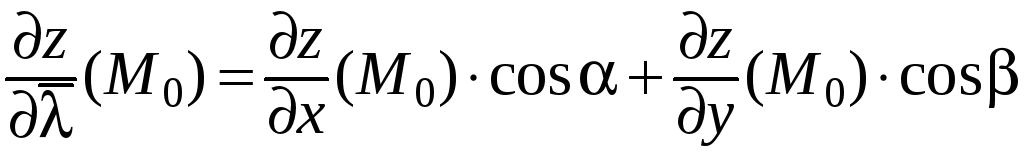Сумму
попарных произведений в правой части
этого равенства можно рассматривать
как скалярное
произведение
в ортонормированном базисе
вектора-градиента grad
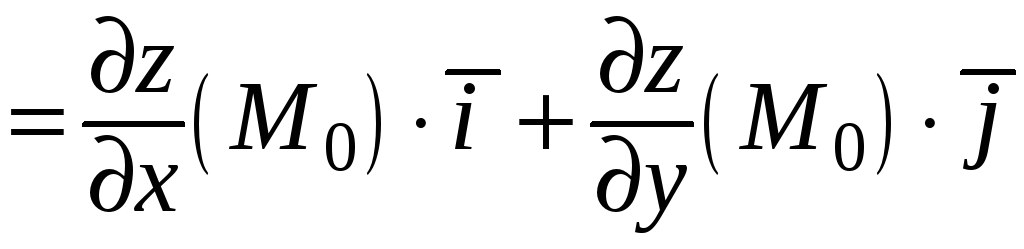в точке
и единичного вектора
,
сонаправленного с вектором
.
Таким образом,
grad
.
(29)
Формула (29) справедлива также для функции трех или более переменных.
Пусть
grad
,
и
― угол между вектором grad
и вектором
(рис. 22). В соответствии с определением
скалярного произведения (поскольку
):
.
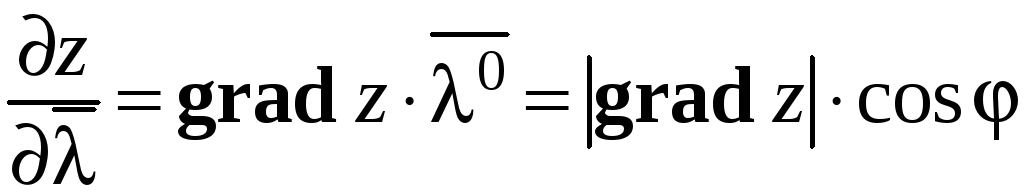Наибольшее
(положительное) значение производной
по направлению вектора
имеем при
,
то есть, когда
;
вектор
в этом случае направлен одинаково с
вектором-градиентом. Итак, градиент
функции в точке
задает направление наибольшей скорости
роста
функции в малой окрестности этой точки.
Аналогично
наименьшее (наибольшее по модулю
отрицательное) значение производной
по направлению вектора
имеем, если
,
то есть при
;
последнее означает, что вектор
направлен противоположно вектору-градиенту.
Итак, вектор,
направленный противоположно градиенту
функции в точке
,
задает направление наибольшей скорости
убывания
функции в малой окрестности этой точки.
Литература
Основная литература
1. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. — М.: Наука, 1988. 431 с.
2. Кузнецов В.О. Теория пределов. — СПб.: СПГУВК. 2003. 43 с.
3. Пискунов Н.С. Дифференциальное и интегральное исчисления, т.1. — М.: Наука, 1978. 456 с; т. 2— М.: Наука, 1978. 576 с.
Дополнительная литература
4. Ястребов М.Ю. Производная и исследование функций. СПб.: СПГУВК. 2003. — 45 с.
5. Ястребов М.Ю. Математика. Неопределенный и определенный интегралы. СПб.: СПГУВК. 2004. — 55 с.
6. Кузнецов В.О., Ланева И.В., Ястребов М.Ю. Математический анализ. Конспект лекций для 1 семестра. СПб.: СПГУВК. 1997. — 131 с.
7. Ястребов М.Ю., Кузнецов В.О., Пижурина Н.Ф. Математический анализ. Конспект лекций для III семестра. СПб.: СПГУВК. 1999. — 102 с.
ОГЛАВЛЕНИЕ
1. Понятие функции нескольких переменных …….…………..3
2. Предел функции нескольких переменных …….……………6
3. Приращения функции нескольких переменных ……………7
4. Непрерывность функции нескольких переменных …….…..8
5. Частные производные …….……………………………….....9
6. Дифференцируемость……………………………………….12
7. Частные производные сложной функции …….…………...18
8. Полная производная сложной функции …….……………..21
9. Дифференцирование неявной функции …….……………..24
10. Уравнение касательной к пространственной линии ….…..27
11. Уравнение касательной плоскости к поверхности …….….30
12. Частные производные высших порядков …….……………34
13. Экстремумы …….……………………………………………36
14. Производная по направлению и градиент …….…………...39
Литература…………………….…………………….…………...47