7. Частные производные сложной функции
Пусть
в области
задана функция двух переменных:
,
(6)
у
которой переменные
и
в свою очередь являются функциями
переменных
и
:
,
(7)
заданными
в области
.
Тогда
является сложной функцией независимых
переменных
и
с промежуточными переменными
и
:
.
(8)
Рассмотрим
задачу нахождения частных производных
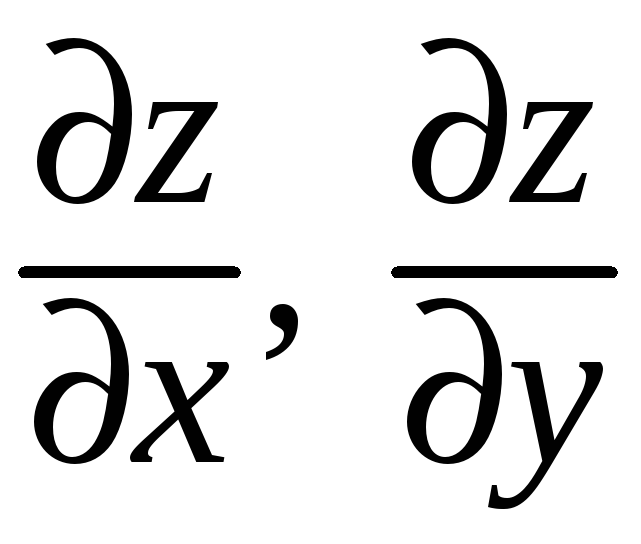этой сложной функции без использования
явной записи (8).
Пусть
точка
,
и функции
и
,
согласно уравнениям (7), переводят ее в
точку
:
.
Теорема. Пусть выполняются три условия:
1.
В окрестности точки
существуют частные производные
,
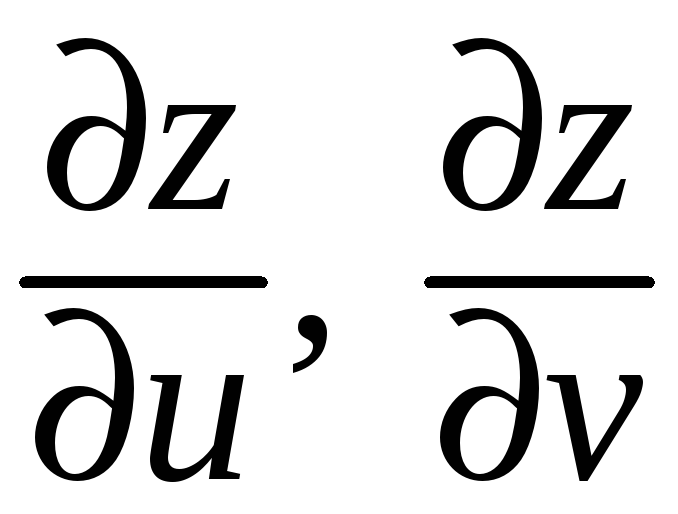непрерывные в самой точке
.
2.
В точке
существуют частные производные
.
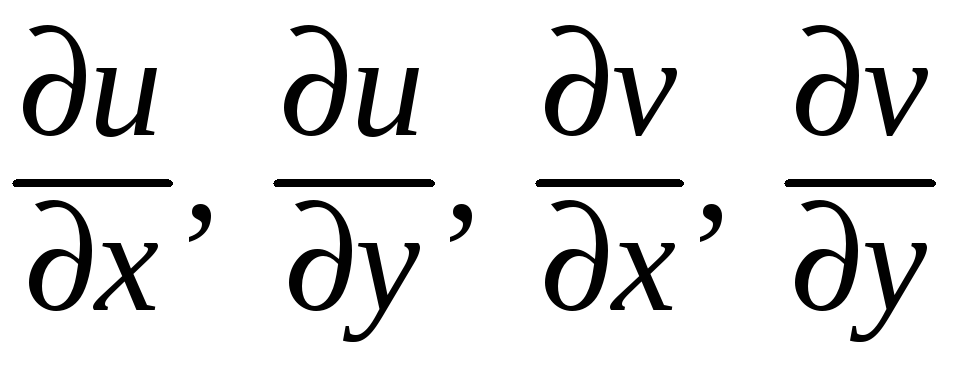3.
Функции
непрерывны в точке
.
Тогда
в точке
существуют частные производные сложной
функции
,
и для них справедливы формулы:
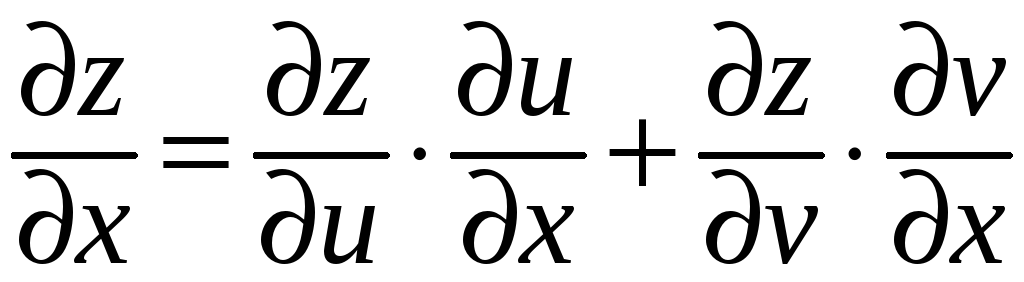
(9)
,
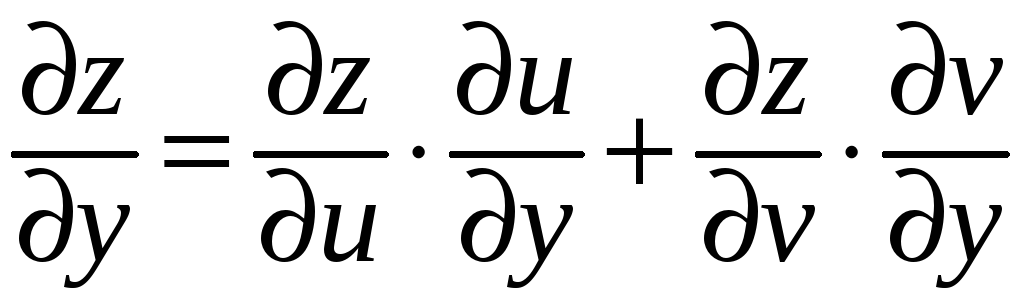или в другой записи:
.
Доказательство.
Проведем его для частной производной
.
Придадим переменной
в точке
приращение
;
оно вызовет частные приращения
промежуточных переменных
,
которые в свою очередь вызовут частное
приращение
сложной функции
.
В силу непрерывности частных производных
(условие 1) к приращению
применима формула (4):
,
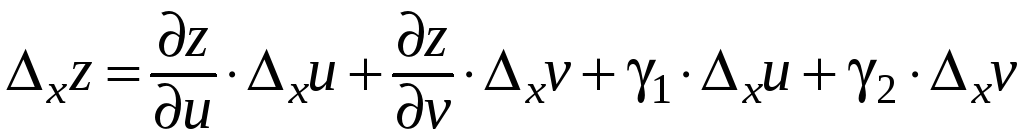откуда,
деля на
,
получаем:
.
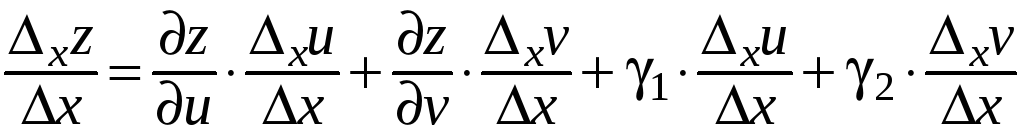(10)
Здесь
— постоянные величины для фиксированной
точки
.
Далее, в силу непрерывности функций
(условие 3):
,
,
а
тогда и величины
в представлении (10) также стремятся к
нулю.
Переходя
в равенстве (10) к пределу при
,
получаем на основании свойств предела
и условия 2:
,
и далее,
.
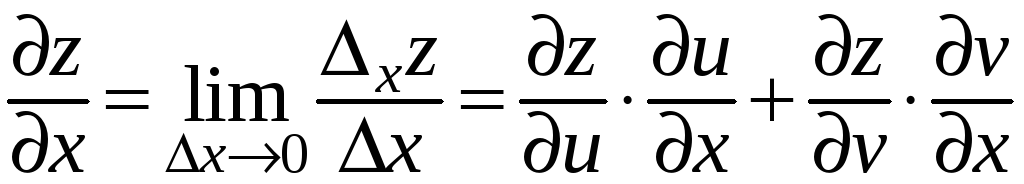Замечание. Аналогичные формулы имеют место для функций большего числа переменных. Например, в ситуации:
,
и
,
,
,
,
имеем:
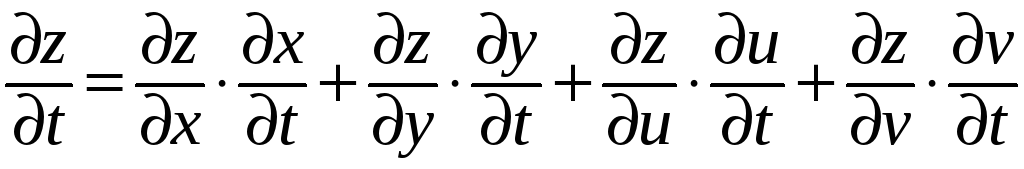
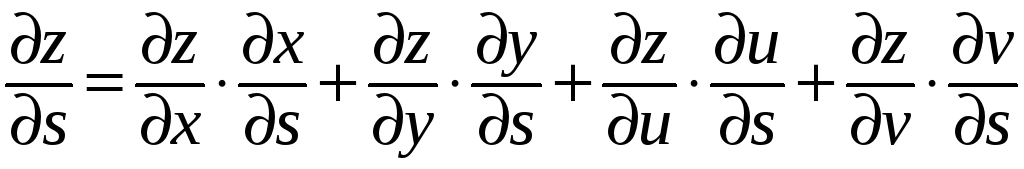
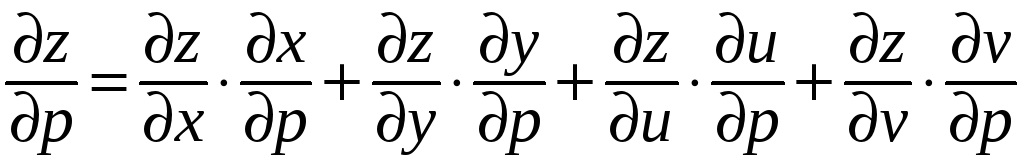
Пример. Пусть
;
.
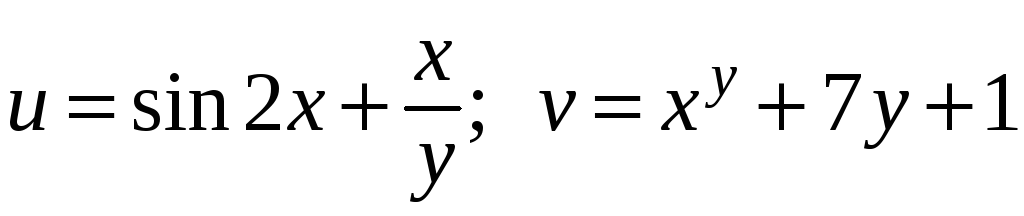Тогда
;
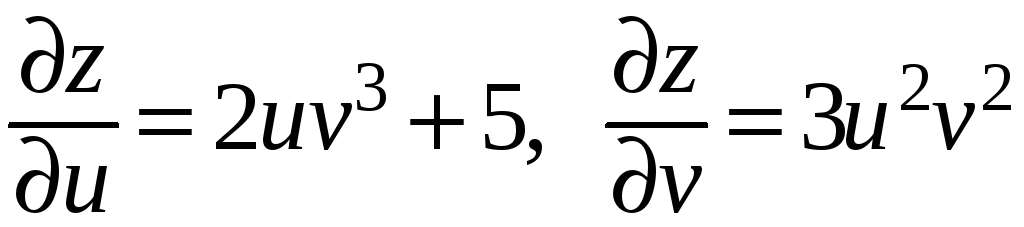далее,
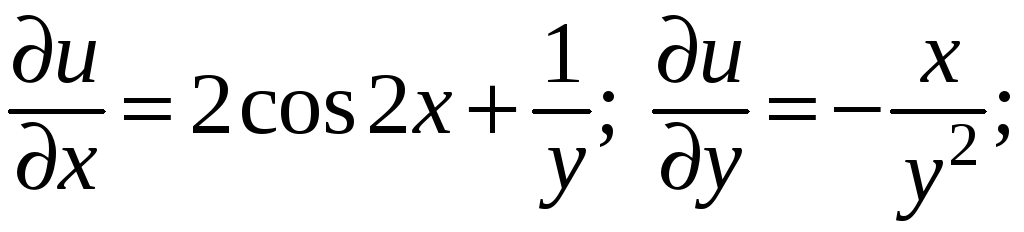
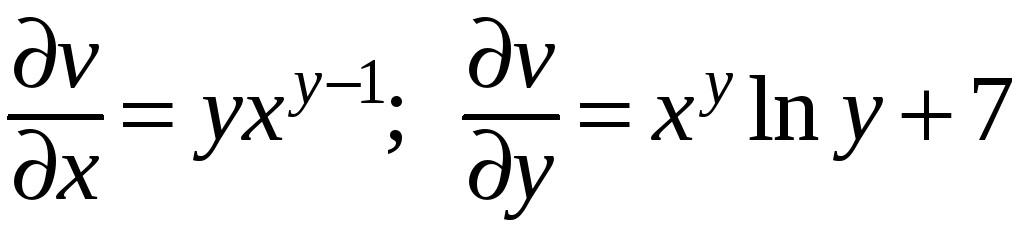
Поэтому
;
.
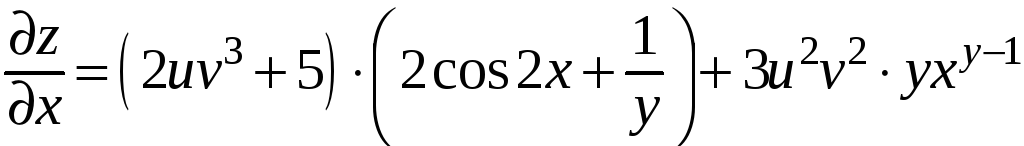8. Полная производная сложной функции
Пусть
в области
задана функция двух переменных:
,
(11)
у
которой переменные
и
являются функциями одной переменной
:
.
(12)
Тогда
является сложной функцией одной
независимой переменной
с промежуточными переменными
и
:
(13)
(рис. 10).
Р
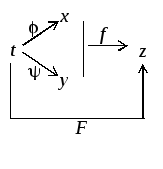
Рассмотрим
задачу нахождения производной
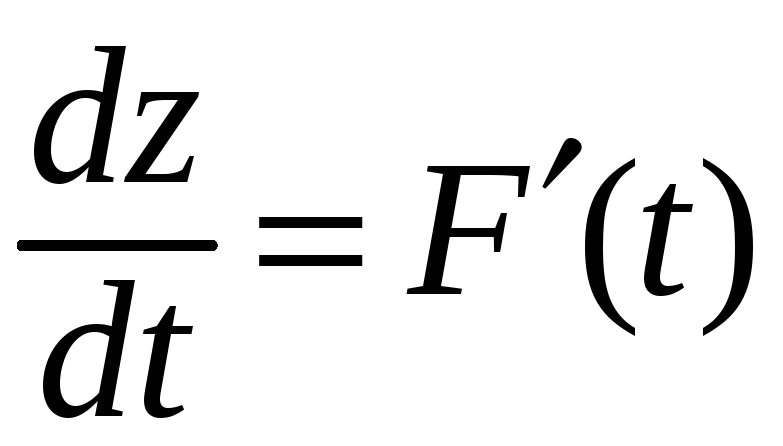этой сложной функции на основании
уравнений (11 и (12) без использования
явной записи (13).
Теорема.
Пусть
,
и
функция
удовлетворяет
двум условиям:
1.
В окрестности точки
существуют частные производные
,
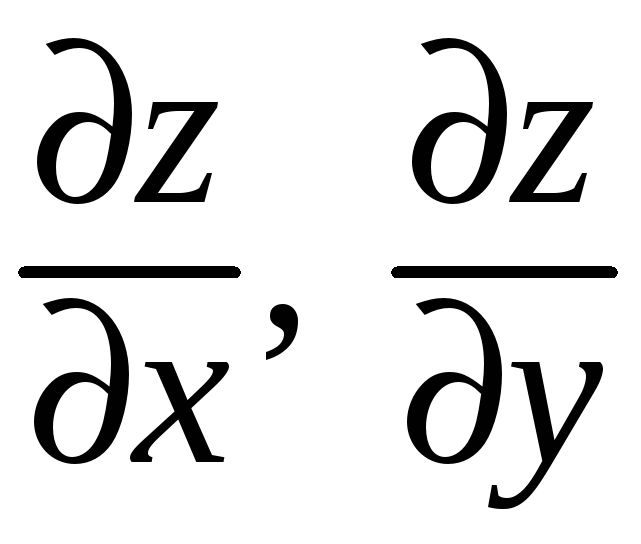непрерывные в самой точке
.
2.
Функции
дифференцируемы
в точке
.
Тогда
сложная функция
дифференцируема в точке
,
и для ее производной справедлива
формула:
.
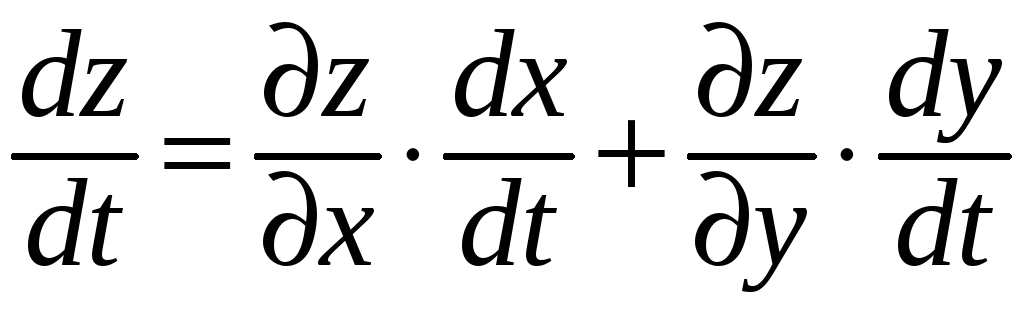(14)
Доказательство.
Придадим
независимой переменной
в точке
приращение
;
оно вызовет приращения
промежуточных переменных
,
которые в свою очередь вызовут приращение
сложной функции
.
В силу непрерывности частных производных
(условие 1) к приращению
применима формула (4):
,
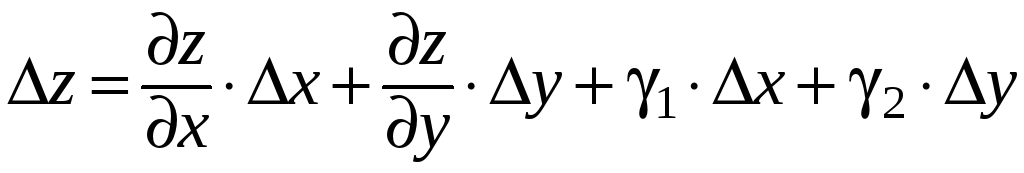откуда,
деля на
,
получаем:
.
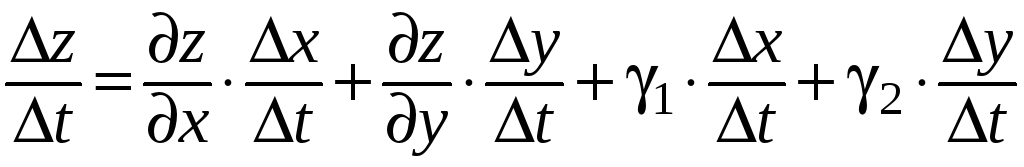(15)
Здесь
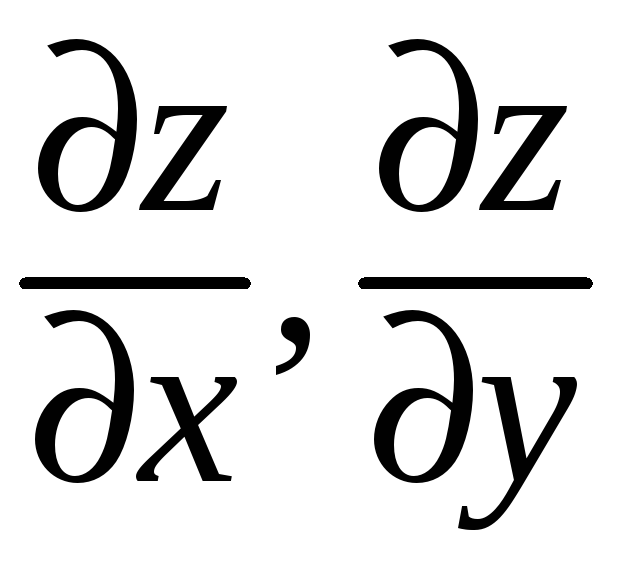— постоянные величины для фиксированной
точки
.
Далее, функции
,
будучи дифференцируемыми в точке
,
являются также и непрерывными в этой
точке, так что
,
,
а
тогда и величины
в представлении (15) также стремятся к
нулю.
Переходя
в равенстве (15) к пределу при
,
получаем:
,
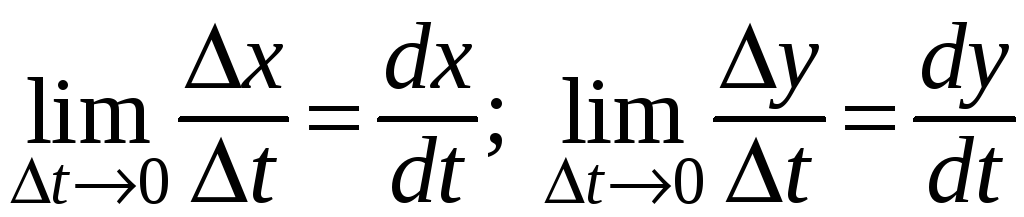и далее, на основании свойств предела:
.
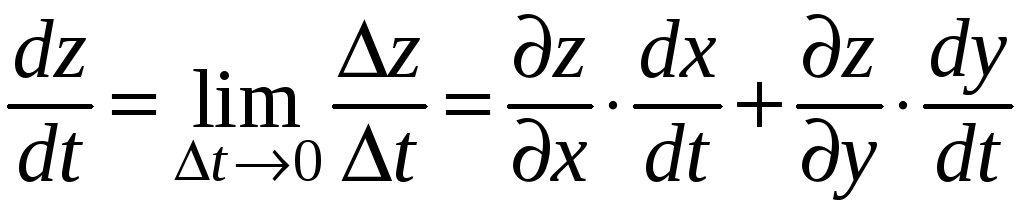Пример.
Пусть
,
где
.
Тогда
.
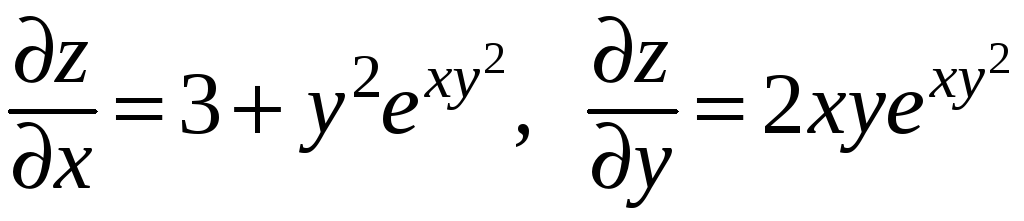Далее,
.
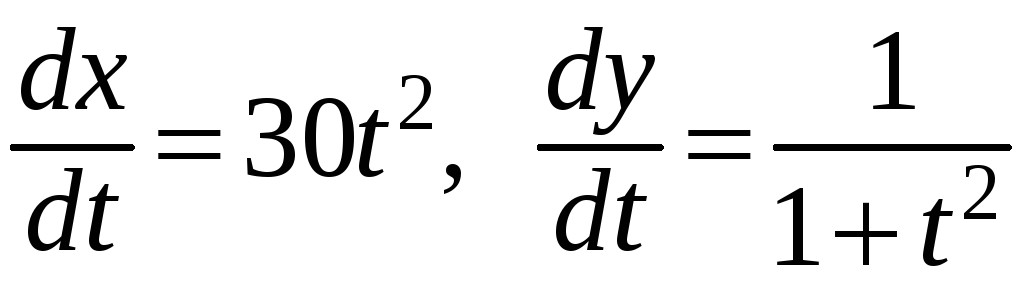Поэтому
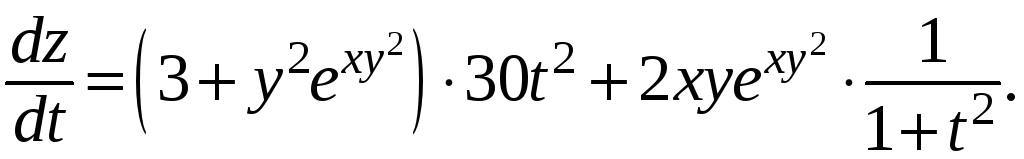
Рассмотрим
теперь случай, когда у функции двух
переменных
одна из переменных, например
,
является функцией другой:
.
Тогда
оказывается сложной функцией от
с двумя промежуточными переменными
и
.
Этот
случай сводится к последней теореме,
если считать, что обе промежуточные
переменные являются функциями одной
независимой переменной
,
которая в этом последнем случае играет
роль переменной
:
,
(16)
,
(17)
так что
,
(18)
причем
функция
в общей схеме (12) является «тождественной»:
.
Формула (14) при этом преобразуется к виду:
.
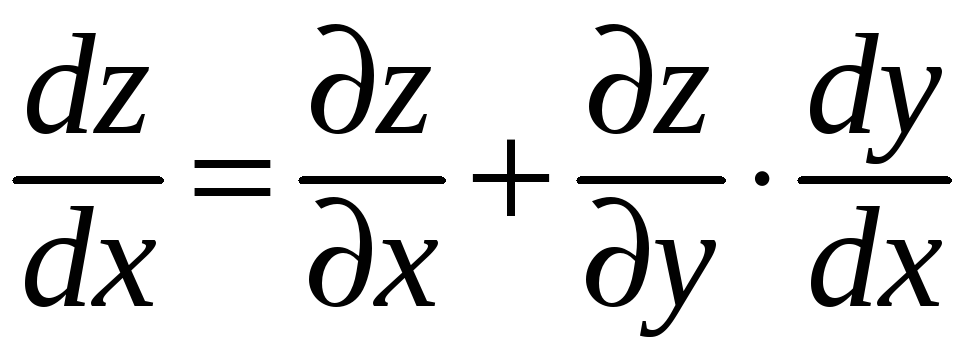(19)
Отметим,
что полная производная
в левой части (19) определяется функцией
(18), а частная производная
в первом слагаемом правой части ―
функцией (16).
Пример.
Пусть
,
причем
.
Тогда
,
,
.
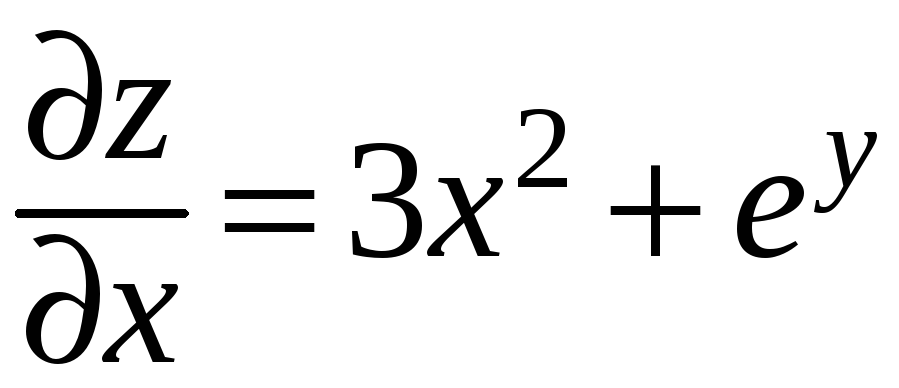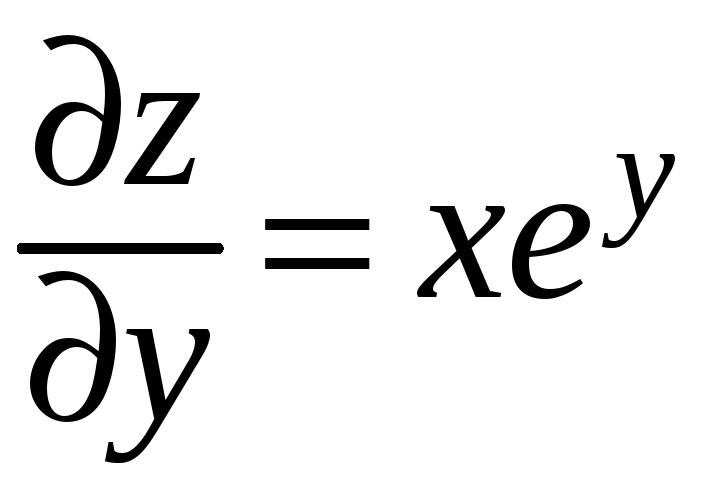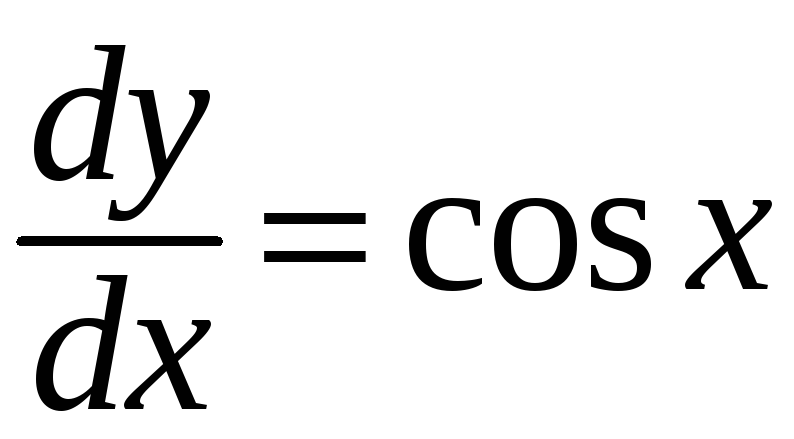Поэтому
.
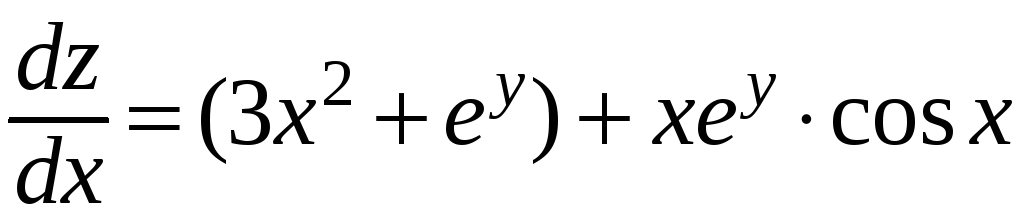