Задачи для самостоятельной работы
Найти общий интеграл уравнений.
40.
.
41.
.
42.
.
Решить задачу Коши
43.
.
44.
.
45.
.
Проинтегрировать уравнения с помощью интегрирующего множителя.
46.
.
47.
.
Решить уравнения с помощью интегрирующих множителей одного из видов:
.
48.
.
49.
.
50.
.
51.
.
2. Типы оду первого порядка, не разрешенных относительно производной
2.1. Основные понятия и определения
Дифференциальное уравнение первого порядка, не разрешенное относительно производной, имеет вид:
. (2.1)
Решение этого
уравнения может быть представлено как
в явном виде:
,
так и в неявном виде:
,
и параметрическом виде:
.
Для уравнений (2.1) так же, как и для уравнений (1.1), разрешенных относительно производной, может ставиться задача Коши и имеет место единственность ее решения. Решение уравнения (2.1) будет частным решением, если в каждой точке его сохраняется единственность решения задачи Коши. Если же в каждой точке решения нарушается единственность решения задачи Коши, то оно будет особым решением.
Кривую подозрительную
на особое решение при условии, что левая
часть уравнения (2.1) непрерывна по
совокупности переменных
и имеет частную производную по
,
можно найти путем исключения
из системы:
. (2.2)
Эта кривая называется дискриминантной кривой уравнения (2.1) и для того, чтобы она была особым решением этого уравнения необходимо, чтобы она была его решением и в каждой ее точке нарушалась единственность решения задачи Коши.
2.2. Построение общего интеграла уравнения n-ой степени
Рассмотрим
уравнение, в котором левая часть
представлена полиномом n-ой
степени относительно
:
.
(2.3)
Такое
уравнение называется уравнением первого
порядка n-ой степени.
Если удается разрешить его относительно
,
то можно получить т (т
п) вещественных решений
. (2.4)
Если для каждого из полученных уравнений (2.4) удается найти общий интеграл
,
то совокупность всех этих интегралов называют общим интегралом уравнения (2.3). Это общий интеграл можно записать в виде одного соотношения
,
в котором левая часть есть полином т-ой степени относительно произвольной постоянной С.
2.3. Уравнения, квадратные относительно
Такие уравнения имеют вид:
, (2.5)
и их можно решить
относительно
:
. (2.6)
Эти уравнения заданы в области p2 – q 0. Интегрируя уравнения (2.6), найдем общий интеграл уравнения (2.5).
Особым решением уравнения (2.5) может быть только дискриминантная кривая:
p2 – q = 0,
получающаяся
исключением
из системы:
.
Пример 33. Найти общий интеграл уравнения:
.
▲Решая исходное
уравнение относительно
,
получим
Решая каждое из этих уравнений в отдельности, получаем их общие интегралы:
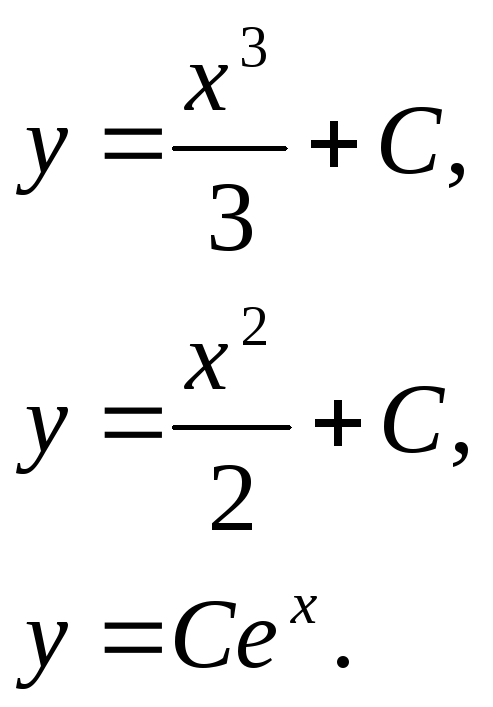
Следовательно, общий интеграл исходного уравнения будет иметь вид:
.▲
Пример 34. Найти общий интеграл уравнения:
и определить имеет ли это уравнение особое решение.
▲ Решая исходное
уравнение относительно
,
получим
.
Интегрируя это уравнение, найдем
Откуда получаем
общий интеграл:
.
Он представляет
собой семейство окружностей с центрами
в точках
и радиусом равным С.
Особым решением
может быть только дискриминантная
кривая
,
которая распадается на прямые у = х
и у = -х.
Полупрямые у = х, х 0 будут особыми решениями. Они являются огибающими семейства окружностей. ▲