Задачи для самостоятельной работы

1. Найти общий интеграл уравнения:

.

2. Найти решения уравнения: .

3. Проинтегрировать уравнение:.

4. Проинтегрировать уравнение:.

5. Решить задачу Коши: .

6. Найти решение уравнения: 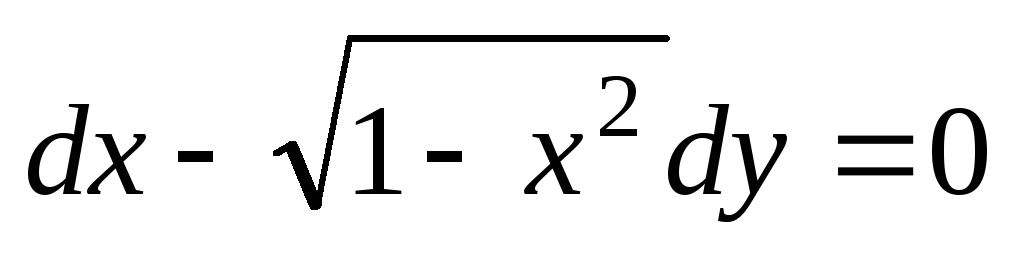и выделить интегральную кривую, проходящую через точку .

7. Найти решение уравнения: , выделить интегральную кривую, проходящую через точку , выяснив предварительно вопрос о существовании и единственности этой интегральной кривой.

8. Составить дифференциальное уравнение заданного семейства кривых: а) 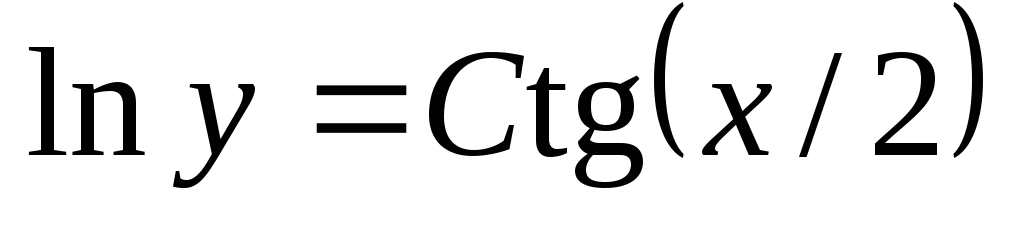; б) .

1.4. Уравнения, приводящиеся к уравнениям с разделяющимися переменными

Рассмотрим уравнение вида

M(x,y)dx + N(x,y)dy = 0 . (1.28)

Если в этом уравнении коэффициенты M(x,y) и N(x,y) являются однородными функциями одного и того же измерения, т.е. выполняются тождества:

и ,

то такое уравнение будет называться однородным и его переменные разделяются посредством подстановки y = zx, где z есть новая неизвестная функция от x. После ее подстановки, а также подстановки значения ее дифференциала: , в уравнение (1.28), получим

обозначив , получим уравнение

, (1.29)

предполагая, что z)0, приходим к уравнению , после интегрирования которого, получим общий интеграл уравнения (1.28)

или ,

где ,

или, возвращаясь к искомой функции у, заменив z на , получим общий интеграл уравнения (1.28): .

В процессе разделения переменных пришлось делить на х и , поэтому необходимо рассмотреть еще два уравнения

х =0 и =0. (1.30)

Первое определяет решение уравнения (1.29), которое может оказаться решением уравнения вида

и тогда, после включения начала координат, должно быть присоединено к решениям уравнения (1.28).

Если второе уравнение из (1.30) имеет действительные решения вида z=a=const, то им соответствуют в силу подстановки y=zx решения однородного уравнения (1.28) вида

(х0)

Эти полупрямые, как и полуоси оси у, о которых шла речь выше, могут оказаться особыми решениями однородного уравнения (1.28).

Пример 7. Найти решение уравнения:

.

▲Это уравнение является однородным уравнением, т.к. коэффициенты при dx и dy есть однородные функции одного и того же измерения, то есть и . Следовательно, его можно решить, использовав подстановку y=zx. Вычислив dy=xdz+zdx, и подставив в исходное уравнение, получим

.

Сокращая на x² и собирая члены, содержащие dx и dy, получим

.

Далее разделяя переменные и интегрируя, найдем

и, возвращаясь к искомой функции у, в конечном итоге получим

.

Это есть общий интеграл исходного уравнения.

При разделении переменных пришлось сокращать на х² и делить на (z³+z), поэтому необходимо рассмотреть еще два уравнения, а именно х² =0 и (z³+z)=0. Первое уравнение дает х = 0, но полуоси у (х = 0 (у 0)) не являются решениями исходного дифференциального уравнения. Из второго уравнения находим z=0 и, подставляя в y=zx,получим

y =0 (x0).

Эти полуоси оси х являются решениями исходного уравнения. Эти решения частные, т.к. во всех точках имеет место единственность решения задачи Коши. ▲

Уравнение вида

, (1.31)

где a,b,c,a₁,b₁,c₁, - постоянные, и для которых выполняется условие

, (1.32)

можно привести к однородному уравнению посредством замены переменных

, (1.33)

где  и  - новые переменные, а  и  - некоторые постоянные числа, определяемые из системы

. (1.34)

В результате получим уравнение вида

. (1.35)

Если же условие (1.32) не выполняется, т.е.

, (1.36)

то исходное уравнение (1.31) может быть переписано в виде

, (1.37)

в котором переменные можно разделить с помощью подстановки z=ax+by, где z – новая неизвестная функция от x.

Пример8. Найти решение уравнения

. (1.38)

▲Проверим, выполняется ли условие (1.32)

.

Следовательно, можно записать систему (1.34)

, решив которую, можно определить  и. Таким образом, уравнения (1.33) принимают вид:

. (1.39)

Откуда dx=d, а dy=d. Следовательно, внося полученные значения x, y, dx, dy в исходное уравнение получим:

или же . (1.40)

У полученного уравнения (1.40) могут оказаться такие решения, которых нет у исходного уравнения (1.38). Таковыми могут быть лишь те функции, которые обращают в нуль тот множитель, на который мы помножили обе части исходного уравнения.

В данном случае множитель ( обращается в нуль лишь одной функцией , которая не является решением уравнения (1.40).

Уравнение (1.40) есть однородное уравнение, поэтому его можно решать, используя подстановку: =z, которая приводит к уравнению

.

В данном уравнении можно разделить переменные. При этом получается уравнение вида:

, (1.41)

интегрируя которое, получаем

. (1.42)

Это есть общий интеграл уравнения (1.41).

Далее подставляем вместо z его выражение , получим общий интеграл уравнения (1.40):

или .

Далее и надо заменить согласно равенствам (1.39)

,

после чего общий интеграл исходного уравнения (1.38) принимает вид:

.▲

Пример 9. Решить уравнение

. (1.42)

▲Проверим, выполняется ли условие (1.32)

.

Таким образом, условие (1.32) не выполняется, однако выполнено условие (1.36). Следовательно, исходное уравнение (1.42) можно записать в виде (1.37), а именно

. (1.43)

Введем подстановку z=x-2y, откуда вычислим и

.

Подставляя значения у и в уравнение (1.43), получим:

,

и после преобразований будем иметь:

. (1.44)

Интегрируя это уравнение, получим его общий интеграл: , а возвращаясь к исходным переменным запишем общий интеграл уравнения (1.42):

.▲

Некоторые ОДУ первого порядка можно привести к однородным уравнениям с помощью замены , где k –число подлежащее определению. Такие уравнения называются обобщенными однородными уравнениями.

Пример 10. Привести уравнение вида к однородному уравнению.

▲Сделаем замену, после которой исходное уравнение принимает вид:

.

Это уравнение будет однородным в случае равенства всех степеней его членов, а именно 4+(2k-1)=4k=6. Эти равенства будут выполняться только при k=3/2, поэтому замена приведет исходное уравнение к однородному ОДУ вида:

,

которое решается с помощью подстановки z=ux, где u –новая неизвестная функция от х, с учетом того, что будем иметь

,

или после сокращения на х⁶ получим

.

Разделив переменные, придем к уравнению , в результате интегрирования которого, получим

.

Возвращаясь к искомой функции у окончательно запишем общий интеграл исходного уравнения

.▲

Пример 11. Найти общий интеграл уравнения:

.

▲Это уравнение не является однородным, но с помощью замены мы придем к уравнению вида

.

Функции 2kz^k-1 и (x-4z^k/2) этого уравнения являются однородными и имеют одну и ту же степень при k=2. Следовательно, исходное уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки y=x²u(x)

, (х0).

Проинтегрировав это уравнение, получим вид общего интеграла или, возвращаясь к искомой функции у, получим общий интеграл исходного уравнения

.▲