Министерство образования Российской федерации

Петрозаводский государственный университет

Кольский филиал

«ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА»

Учебно-методическое пособие

Апатиты

2002

УДК 517

Обыкновенные дифференциальные уравнения первого порядка. /Учебно-методическое пособие для решения задач. //составил к.т.н. - Терещенко С.В./ –Апатиты.: Издание КФ ПетрГУ., 2003. –70 с.

Пособие охватывает такие следующие разделы темы: уравнения с разделяющимися переменными и уравнения, приводящиеся к ним, однородные и неоднородные линейные уравнения и приводящиеся к ним, уравнения в полных дифференциалах и использование интегрирующего множителя, приводящего исходные уравнения к уравнениям с разделяющимися переменными и к уравнениям в полных дифференциалах, уравнения, неразрешенные относительно производных.

В каждом параграфе приводятся необходимые теоретические сведения. Типовые задачи даются с подробными решениями. Имеются задачи для самостоятельной работы с ответами. Варианты контрольных работ, содержащиеся в пособии, могут быть использованы как для работы со студентами очного, так и заочного отделения.

Рецензенты:

кафедра высшей математики филиала Санкт-Петербургского инженерно-экономического университета в г. Апатиты, заведующий кафедрой высшей математики филиала, .доктор физико-математических наук Мингалев В.С.;

кафедра информационных систем Кольского филиала Петрозаводского государственного университета, профессор, доктор технических наук Богатиков В.Н.

Печатается по решению редакционно-издательского совета Петрозаводского государственного университета в качестве учебно-методического пособия

© Издательство Петрозаводского

Государственного университета

Кольский филиал,2003

Содержание

СОДЕРЖАНИЕ 3

Введение 4

1. Типы оду первого порядка, разрешенных относительно производной 4

1.1. Основные понятия и определения 4

1.2. ОДУ, не содержащие искомой функции, и ОДУ, не содержащие независимой переменной 10

1.3. Уравнения с разделяющимися переменными 12

Задачи для самостоятельной работы 14

1.4. Уравнения, приводящиеся к уравнениям с разделяющимися переменными 14

Задачи для самостоятельной работы 21

1.5. Линейные уравнения и уравнения, приводящиеся к ним 22

Задачи для самостоятельной работы 37

1.6. Уравнения в полных дифференциалах 38

Задачи для самостоятельной работы 49

2. Типы оду первого порядка, не разрешенных относительно производной 50

2.1. Основные понятия и определения 50

2.2. Построение общего интеграла уравнения n-ой степени 51

2.3. Уравнения, квадратные относительно 52

2.4. Неполные уравнения 53

2.5. Уравнение Лагранжа 59

2.6. Уравнение Клеро 62

Задачи для самостоятельной работы 65

Ответы на задачи самостоятельной работы 67

Контрольные задания 70

Список использованных источников 73

Введение

При исследовании какого-либо процесса - естественнонаучного, экономического или социального, как правило, не удается непосредственно найти законы, связывающие величины характеризующие исследуемые явления. Однако, при этом достаточно легко устанавливается взаимосвязь между этими величинами и их производными или дифференциалами. Соотношения такого рода и называются дифференциальными уравнениями (ДУ). Уравнения, содержащие производные по многим независимым переменным, называются уравнениями в частных производных. Уравнения, содержащие производные лишь по одной из независимых переменных, называются обыкновенными дифференциальными уравнениями (ОДУ). Поэтому дифференциальные уравнения являются одним из основных математических понятий, наиболее широко применяемых при решении различных практических задач.

1. Типы оду первого порядка, разрешенных относительно производной

1.1. Основные понятия и определения

ОДУ первого порядка, разрешенные относительно производной имеют вид

, (1.1)

где функция f(x,y) однозначная и непрерывна по совокупности переменных х и у в некоторой области на плоскости (х,у). Эта область называется областью определения уравнения (1.1).

Если в окрестности точек (х,у) функция f(x,y) обращается в бесконечность, то в этом случае вместо уравнения (1.1) рассматривается уравнение вида

. (1.2)

Если правую часть уравнения (1.1) можно представить в виде

,

тогда уравнение (1.1) можно записать в форме дифференциалов, а именно

M(x,y)dx + N(x,y)dy = 0. (1.3)

Необходимо отметить, что функции М(x,y), и N(x,y) являются непрерывными функциями в некоторой области изменения переменных x и y.

ОДУ (1.1) и (1.3) равносильны (т.е. имеют одинаковые решения) в области, где M(x,y)0, и наоборот, при переходе от уравнения (1.3) к (1.1) – к решениям ОДУ (1.3) необходимо добавлять решения, на которых M(x,y)=0.

Иногда рассматривают ОДУ в так называемой симметрической форме, а именно

. (1.4)

Требование решить уравнения вида (1.1) и (1.3) соответствует требованию нахождения всех функций вида

, х  (a,b), (1.5)

обеспечивающих тождество

, (1.6)

для всех х из интервала (a,b), причем эти функции должны быть определены и непрерывно дифференцируемые в этом интервале.

Требование решить ОДУ (1.2) понимается, как требование найти все функции вида

, у (c,d), (1.7)

которые реализуют тождество

, (1.8)

для всех у из интервала (c,d).

Для ОДУ первого порядка (1.1) имеет место теорема, которая гласит о том, что если в уравнении (1.1) с начальными данными х₀, у₀, функция f(x,y) удовлетворяет двум условиям:

1. f(x,y) определена и непрерывна по обеим переменным в некоторой замкнутой области R

R : х – х₀ а, у – у₀ в

где а и в- некоторые положительные числа, а из условия непрерывности функции в замкнутой области следует и то, что она должна быть еще и ограниченной функцией, т.е. должно существовать такое М, что

 f(x,y) М , (1.9)

для всех точек области R;

2. f(x,y) в области R удовлетворяет условию Липшица^ по переменной у, т.е.

 f(x,y₁) - f(x,y₂) L y₁ - y₂, (1.10)

где L – постоянная Липшица, тогда существует единственное решение у(х) уравнения (1.1), удовлетворяющее начальному условию

у(х₀) = у₀ , (1.11)

определенное и непрерывно дифференцируемое для значений х в интервале (х–х₀)h, где h=min, и не выходящее при этих значениях х из области R.

Эта теорема имеет простую геометрическую интерпретацию. Ее можно сформулировать так: если условия теоремы выполнены, то: через каждую точку (х₀, у₀) области R проходит кривая, и притом только одна. Такую кривую будем называть интегральной кривой.

Задача о нахождении решения уравнения (1.1), удовлетворяющего начальному условию (1.11), называется задачей Коши.

Пусть задана некая функция вида

, (1.12)

определенная в некоторой области изменения переменных х и С и имеет производную по х.

Эта функция будет называться общим решением уравнения (1.1) в области R изменения переменных х и у, если:

1. через каждую точку некой области D изменения переменных x и С проходит интегральная кривая уравнения (1.1), и притом, единственная;

2. для каждой точки (х, у)  R уравнение (1.12) решается относительно С, так что в результате получается ;

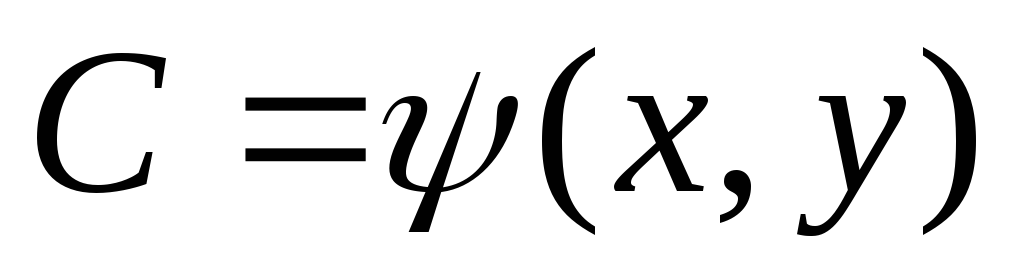3. функция 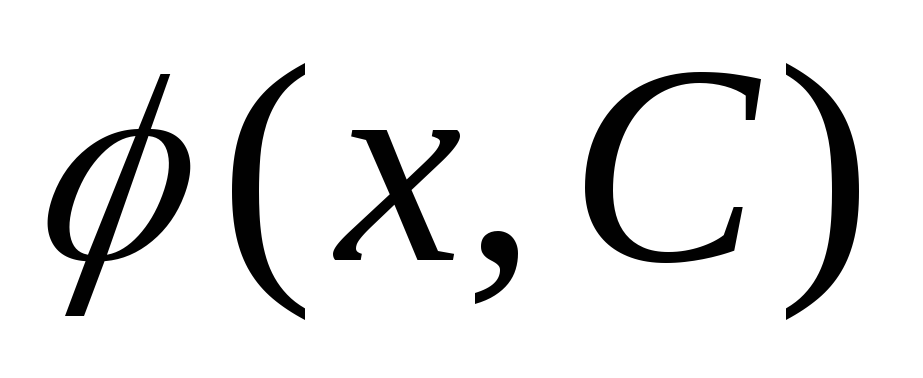из семейства (1.12), отвечающая каждому С, является решением уравнения (1.1).

Если общее решение уравнения (1.1) задано в неявном виде, т.е.

F(x,y,C) = 0 , (1.13)

то оно называется общим интегралом этого уравнения.

Решение, в каждой точке которого задача Коши имеет единственное решение, то есть, выполняются условия теоремы существования и единственности решения задачи Коши, называется частным решением. Каждое решение, содержащееся в общем решении, обладает этим свойством, следовательно, является частным решением.

Необходимо отметить, что ОДУ может иметь такое решение, которое не содержится в общем решении, и не является частным решением. Такое решение получило название особого решения, т.к. в каждой его точке нарушается единственность решения задачи Коши, т.е. через каждую его точку проходит не менее двух интегральных кривых. Особое решение не может быть получено из формулы общего решения (1.12) при конкретном числовом значении произвольной постоянной С (но оно может быть получено при С=С(х)). Оно представляет собой особую линию уравнения (1.1). Однако не всякая особая линия является особым решением. Нарушение единственности решения ОДУ происходит в точках, при приближении к которым, неограниченно возрастает, т.е. в точках, в которых 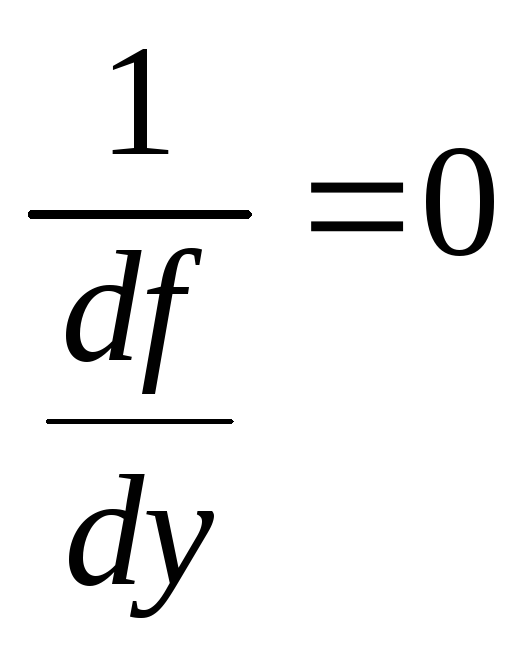. Кривые подозрительные на особые решения, могут быть найдены по уравнению семейства интегральных кривых, заданных или уравнением (1.12) или уравнением (1.13). Если эти уравнения семейства интегральных кривых имеют огибающую, т.е. кривую, обладающую тем свойством по отношению к кривым семейства, что она в каждой своей точке касается хоть одной кривой семейства интегральных кривых, и вся она состоит из точек касания.

Огибающая семейства интегральных кривых уравнения (1.1) всегда является особым решением этого уравнения.

Кривую подозрительную на огибающую семейства интегральных кривых (1.12), можно найти путем исключения параметра С из системы, составленной из уравнений

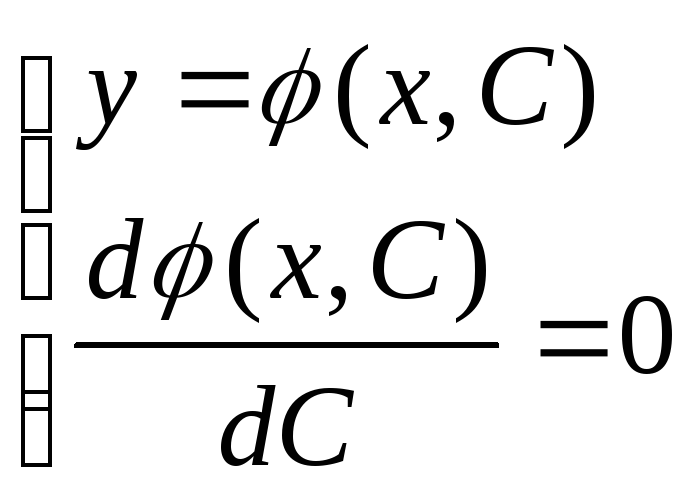. (1.14)

Пример 1. Проверить является ли для уравнения

(1.15)

общим решением функция

. (1.16)

▲ Проверим, выполняются ли условия, характеризующие функцию (1.16) как общее решение уравнения (1.15):

1. через любую точку (х₀, у₀) плоскости хOу проходит единственная интегральная кривая уравнения (1.15):

;

2. уравнение (1.16) решается относительно С для каждой точки (х₀, у₀):

;

3. подставляя полученное значение С, получаем из (1.16) решение данного уравнения:

.

Таким образом, мы убедились в том, что (1.16) есть общее решение уравнения (1.15). ▲

Пример 2. Найти решения уравнения .

▲Правая часть этого уравнения определена и непрерывна для всех значений х и у, но частная производная обращается в бесконечность при у=0, т.е. во всех точках оси Ох. Для исходного уравнения равенство 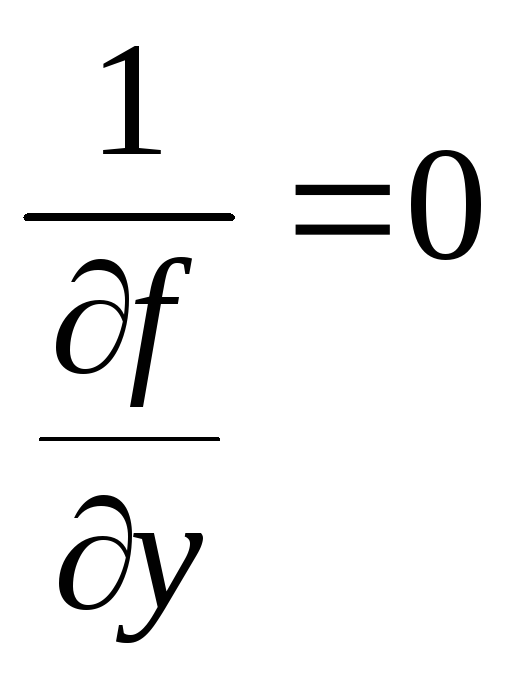имеет вид: 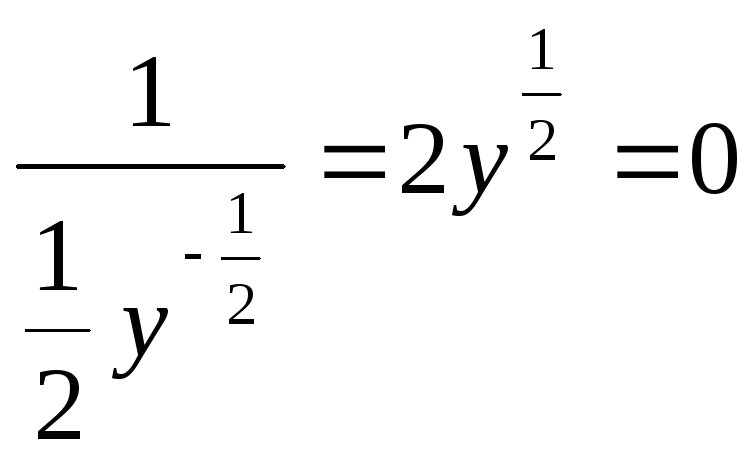или же у=0. Очевидно, что у=0 есть решение исходного уравнения, но является ли оно особым? Для этого необходимо проверить, нарушается ли единственность или нет.

Общее решение исходного уравнения можно получить, если привести его к виду: . В результате интегрирования этого уравнения получим уравнение семейства интегральных кривых: или . Это уравнение выражает правую «половину» параболы, которая в точке х = -С касается оси Ох. Таким образом, через каждую точку оси Ох проходит две интегральные кривые: сама ось Ох и ветвь параболы. Значит, ось Ох (интегральная кривая у=0) есть особое решение для исходного уравнения.

Проверим, является ли интегральная кривая у=0 огибающей семейства интегральных кривых . Для этого составим систему (1.14)

.

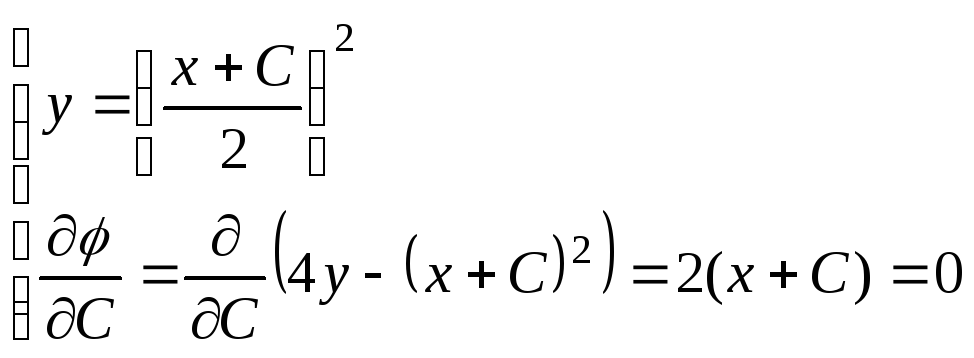Исключая С из этой системы, установим, что кривой, подозрительной на огибающую будет являться ось Ох, т.е. у 0. ▲

Пример3. Найти особые решения уравнения:

.

▲Правая часть этого уравнения непрерывна во всей плоскости хОу. Следовательно, единственность может нарушаться лишь за счет нарушения ограниченности частной производной . В этом случае , и уравнение 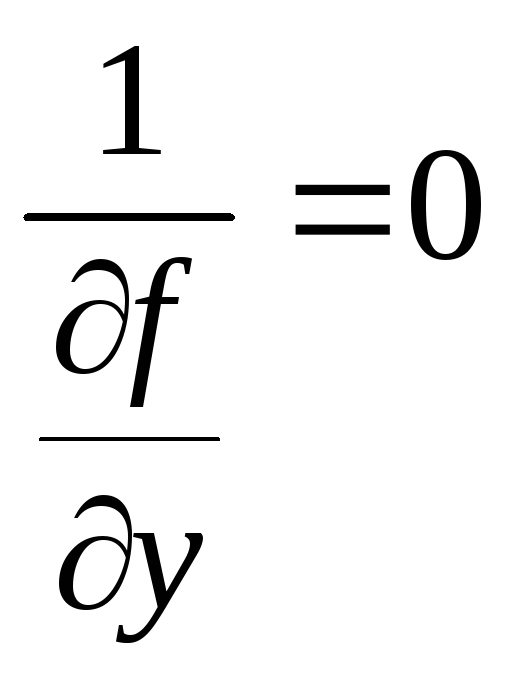имеет вид: или у - х = 0. Определяемая из этого уравнения функция у = х, которая могла бы быть особым решением, не удовлетворяет исходному уравнению, т.к. ее подстановка приводит к соотношению

.

Значит, исходное уравнение особых решений не имеет. ▲