
- •Частина друга. Кінематика вступ до кінематики
- •Розділ 3. Кінематика матеріальної точки
- •3.1. Способи задання руху точки
- •3.2. Кінематичні характеристики руху точки
- •Матеріальної точки
- •3.3. Окремі випадки руху точки
- •3.4. Задачі до розділу 3
- •Розділ 4. Кінематика абсолютно твердого тіла
- •4.1. Найпростіші рухи твердого тіла
- •Тіла навколо нерухомої осі
- •Тіла навколо нерухомої осі
- •Тіла навколо нерухомої осі
- •Тіла навколо нерухомої осі
- •Тіла навколо нерухомої осі
- •Прискорення як векторні величини
- •4.2. Плоскопаралельний рух твердого тіла
- •4.3. Задачі до розділу 4
- •Розділ 5. Кінематика складного руху матеріальної точки і абсолютно твердого тіла
- •5.1. Складний рух матеріальної точки
- •При складному русі
- •5.2. Складний рух твердого тіла
- •Обертального та поступального рухів
- •5.3. Задачі до розділу 5
- •Розділ 6. Кінематика механізмів
- •6.1. Структурний аналіз механізмів та їх класифікація
- •6.2. Кінематичний аналіз плоских важільних механізмів другого порядку однократної рухомості з нижчими кінематичними парами
- •Ланок кривошипно-коромислового механізму
- •Кривошипно-повзункового механізму
- •Кривошипно-кулісного механізму
- •6.3. Кінематичний аналіз плоских механізмів методом графічного диференціювання (кінематичних діаграм).
- •6.3. Механізми для передачі обертального руху
- •6.5. Механізми для передачі обертального руху з гнучкими ланками
- •6.6. Плоскі кулачкові механізми
- •З коливним рухом штовхача
- •(Повернуто на 900 проти годинникової стрілки)
- •6.7. Кінематичний синтез кулачкових механізмів
- •Кулачкового механізму в двз
Т
Рис.
5.1. Додавання швидкостей
При складному русі
еорема 2
(теорема додавання прискорень при
складному русі точки): Вектор абсолютного
прискорення складного руху матеріальної
точки дорівнює геометричній (векторній)
сумі прискорень відносного і переносного
рухів точки та прискорення Коріоліса:
(5.3)![]()
Прискорення
Коріоліса
![]() визначається за формулою
визначається за формулою
(5.4)![]()
і
дорівнює подвоєному векторному добутку
кутової швидкості переносного руху
![]() і відносної швидкості точки
і відносної швидкості точки
![]() .
Його величина дорівнює
.
Його величина дорівнює
(5.5)![]()
Вектор
прискорення Коріоліса перпендикулярний
до площини, яка визначається векторами
![]() ,
,
![]() ,
і напрямлений в той бік, звідки найкоротше
суміщення
,
і напрямлений в той бік, звідки найкоротше
суміщення
![]() з
з
![]() відбувається проти ходу годинникової
стрілки (рис. 5.2).
відбувається проти ходу годинникової
стрілки (рис. 5.2).

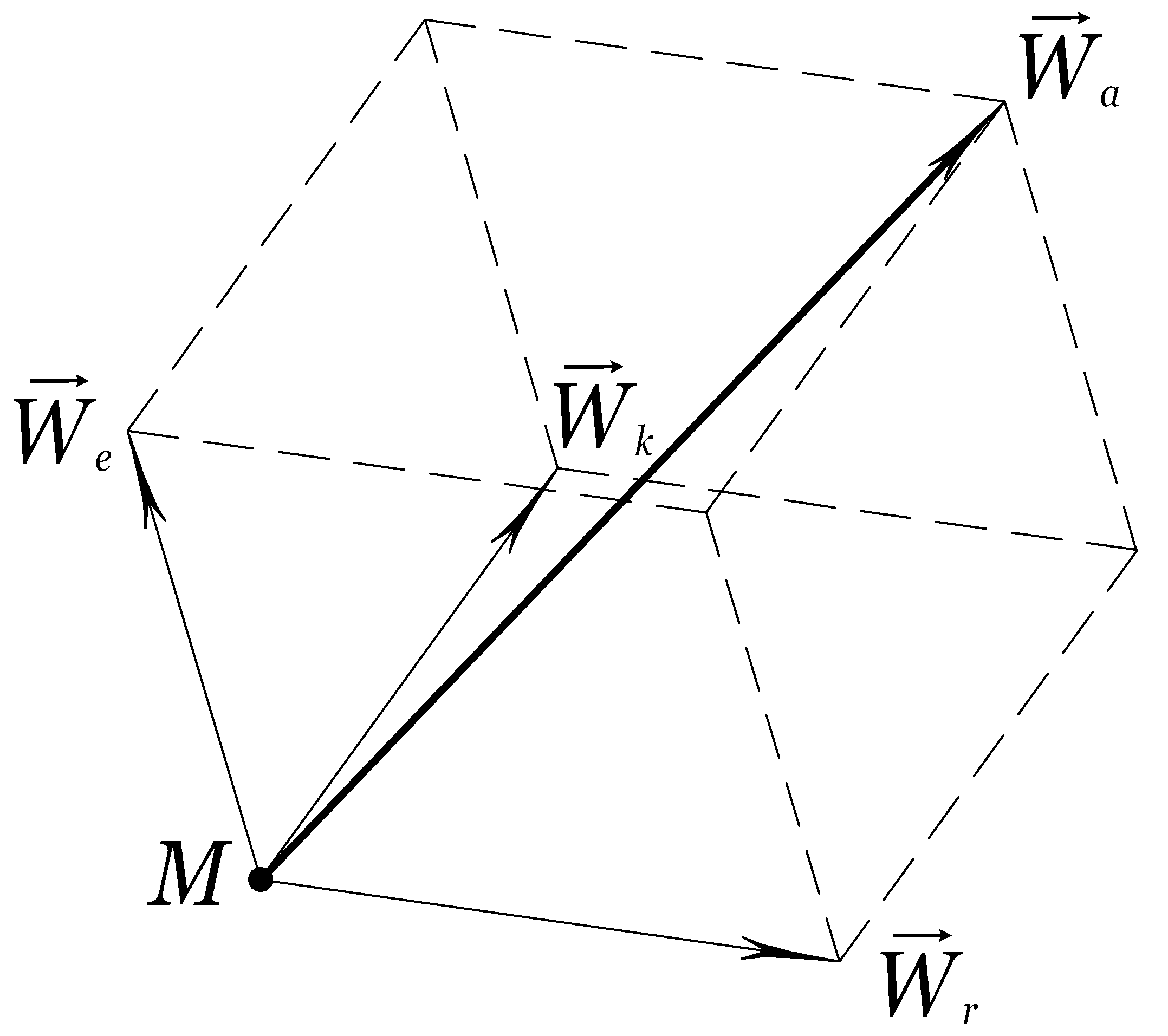
Рис.
5.2. Прискорення
Коріоліса
Рис.
5.3. Додавання прискорень при
складному русі
Із формули (5.5) видно, що прискорення Коріоліса дорівнює нулю в таких випадках:
-
коли
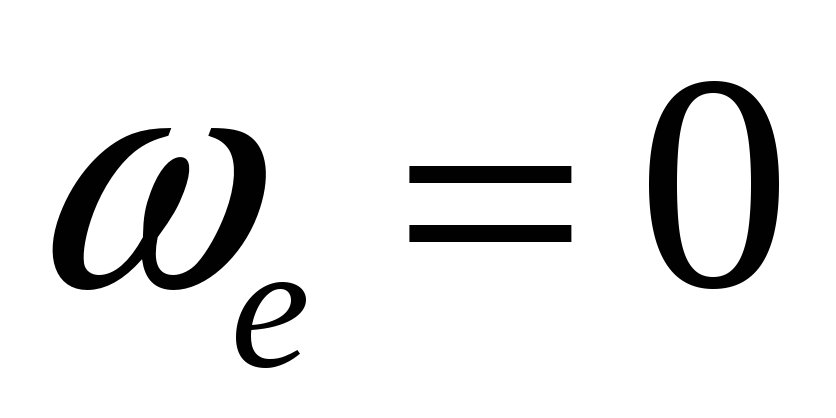 ,
тобто коли переносний рух поступальний
або якщо кутова швидкість переносного
обертального руху в даний момент
дорівнює нулю;
,
тобто коли переносний рух поступальний
або якщо кутова швидкість переносного
обертального руху в даний момент
дорівнює нулю; -
коли
 ,
тобто коли відносна швидкість в даний
момент відсутня;
,
тобто коли відносна швидкість в даний
момент відсутня; -
коли
 або
або
 ,
тобто коли відносний рух відбувається
в напрямку паралельному осі обертання,
або якщо в даний момент
,
тобто коли відносний рух відбувається
в напрямку паралельному осі обертання,
або якщо в даний момент
 та
та
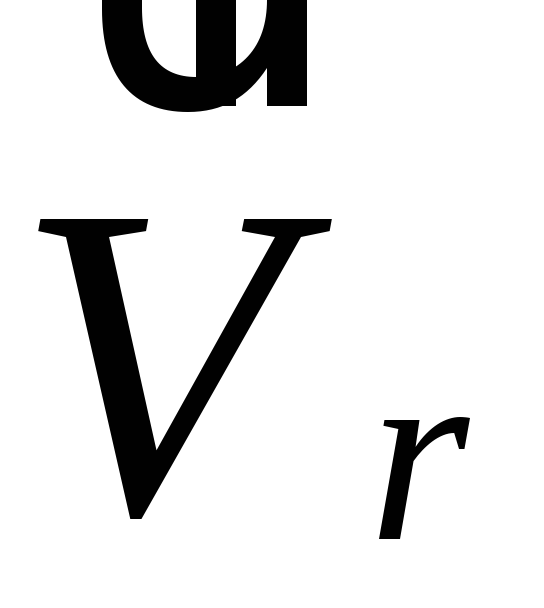 колінеарні.
колінеарні.
Якщо
визначення напрямку абсолютної швидкості
за формулою (5.1) не викликає труднощів,
то при визначенні прискорення
![]() за формулою (5.3) необхідно додавати три
неколінеарні вектори. При цьому величина
і напрямок
за формулою (5.3) необхідно додавати три
неколінеарні вектори. При цьому величина
і напрямок
![]() невідомі (рис. 5.3).
невідомі (рис. 5.3).
При розв’язанні конкретних задач вигідніше замість векторного співвідношення (5.3) використовувати його проекції на осі нерухомої системи координат
(5.6)![]()
![]() ;
;
![]() .
.
В
записі (5.6) вважаються відомими напрямки
проекцій абсолютного прискорення (вони
напрямлені вздовж координатних осей).
Якщо величини
![]() стануть відомі, то величина і напрямок
прискорення
стануть відомі, то величина і напрямок
прискорення
![]() визначається за формулами (3.12).
визначається за формулами (3.12).
5.2. Складний рух твердого тіла
Якщо тверде тіло здійснює рух відносно рухомої системи відліку, а ця система здійснює одночасно переносний по відношенню до нерухомої системи відліку, то результуючий (абсолютний) рух тіла називається складним.
Мета цього підрозділу – встановлення миттєвого розподілу швидкостей точок твердого тіла, який відповідає результуючому складному руху при різних часткових допущеннях про характер відносного і переносного рухів твердого тіла в заданий момент часу.
5.2.1.
Додавання двох поступальних рухів.
Розглянемо тверде тіло, яке перебуває
одночасно в двох незалежних поступальних
рухах з характеристиками (![]() )
та (
)
та (![]() ).
Кожна точка
).
Кожна точка
![]() твердого
тіла здійснює складний рух, тому на
підставі теорем про додавання швидкостей
і прискорень при складному русі (п. 5.1)
маємо, що
твердого
тіла здійснює складний рух, тому на
підставі теорем про додавання швидкостей
і прискорень при складному русі (п. 5.1)
маємо, що
![]() ;
;
![]() .
.
Оскільки ці співвідношення справедливі для всіх точок тіла, тому результуючий його рух буде поступальний.
Отже,
при додаванні двох поступальних рухів
твердого тіла з швидкостями
![]() результуючий рух буде поступальним з
швидкістю
результуючий рух буде поступальним з
швидкістю
![]() .
Цей рух можна визначити рухом однієї
точки тіла.
.
Цей рух можна визначити рухом однієї
точки тіла.
5.2.2.
Додавання обертальних рухів навколо
двох осей, що перетинаються.
Нехай тверде тіло з дійснює
два незалежні обертальні рухи з кутовими
швидкостями
дійснює
два незалежні обертальні рухи з кутовими
швидкостями
![]() відносно нерухомих осей
відносно нерухомих осей
![]() і
і
![]() ,
які перетинаються в
точці
,
які перетинаються в
точці
![]() (рис. 5.4).
(рис. 5.4).
Т
Рис.
5.4. Додавання двох обертальний
рухів навколо осей, що перетинаються
![]() належить одночасно осям
належить одночасно осям
![]() і
і
![]() ,
то її швидкість в будь-який момент часу
дорівнює нулю. Розглянемо точку
,
то її швидкість в будь-який момент часу
дорівнює нулю. Розглянемо точку
![]() ,
яка визначає кінець вектора
,
яка визначає кінець вектора
![]() ,
побудованого за правилом
паралелограма. За теоремою про додавання
,
побудованого за правилом
паралелограма. За теоремою про додавання
швидкостей при складному русі її швидкість дорівнює
![]() .
.
Вектори
![]() та
та
![]() колінеарні , тому
колінеарні , тому
![]() .
Це означає , що в заданий момент часу
точка
.
Це означає , що в заданий момент часу
точка
![]() нерухома. Нерухомою в цей момент часу
буде вісь
нерухома. Нерухомою в цей момент часу
буде вісь
![]() ,
яка визначається точками
,
яка визначається точками
![]() .
Отже, результуючим миттєвим рухом буде
обертання навколо осі
.
Отже, результуючим миттєвим рухом буде
обертання навколо осі
![]() з
деякою кутовою швидкістю
з
деякою кутовою швидкістю
![]() .
.
Розглянемо
довільну точку
![]() тіла.
Визначимо її абсолютну швидкість в
результуючому русі
тіла.
Визначимо її абсолютну швидкість в
результуючому русі
![]() .
.
З цієї рівності визначаємо
(5.7)![]()
Таким
чином, при додаванні обертальних рухів
навколо осей, що перетинаються в точці
![]() ,
результуючим рухом тіла буде миттєвий
обертальний рух навколо осі
,
результуючим рухом тіла буде миттєвий
обертальний рух навколо осі
![]() ,
яка проходить через точку
,
яка проходить через точку
![]() ,
причому кутова швидкість
,
причому кутова швидкість
![]() цього руху дорівнює геометричній сумі
кутових швидкостей
цього руху дорівнює геометричній сумі
кутових швидкостей
![]() складових рухів.
складових рухів.
Миттєва
вісь обертання визначається точкою
![]() і вектором
і вектором
![]() .
З плином часу вісь
.
З плином часу вісь
![]() змінює своє положення, описуючи конічну
поверхню з вершиною в
точці
змінює своє положення, описуючи конічну
поверхню з вершиною в
точці
![]() .
.
Одержані в даному пункті результати можуть бути використані при кінематичному аналізі зубчастих передач і механізмів з конічними зубчастими колесами.
5.2.3.
Додавання двох обертальних рухів
відносно паралельних осей.
Розглянемо випадок коли тверде тіло
здійснює два незалежні миттєві обертальні
рухи з кутовими швидкостями
![]() навколо нерухомих паралельних осей
навколо нерухомих паралельних осей
![]() відповідно.
відповідно.
Результуючим
рухом буде плоскопаралельний рух тіла,
бо швидкості точок, розміщених на прямій,
яка паралельна миттєвим осям обертання,
будуть однакові. Тому достатньо розглянути
миттєвий розподіл швидкостей в довільному
перерізі
![]() тіла площиною
тіла площиною
![]() ,
перпендикулярною
до осей обертання.
,
перпендикулярною
до осей обертання.
Обертання
напрямлені в один бік.
Припустимо, що кутові швидкості
![]() мають однакові напрямки. Позначимо
через
мають однакові напрямки. Позначимо
через
![]() точки перетину фігури
точки перетину фігури
![]() з осями обертання (рис.
5.5).
з осями обертання (рис.
5.5).

Рис. 5.5. Додавання двох однонапрямлених обертальних рухів навколо паралельних осей
В
(5.8)![]() :
:
![]() ;
;
![]() .
.
Напрямки
цих швидкостей зображені на рис.
5.5. Для визначення МЦШ
плоскої фігури
![]() сполучаємо кінцеві точки векторів
сполучаємо кінцеві точки векторів
![]() та
та
![]() .
В перетині з відрізком
.
В перетині з відрізком
![]() одержимо
точку
одержимо
точку
![]() ,
через яку проходить миттєва вісь
обертання.
,
через яку проходить миттєва вісь
обертання.
З
(5.9)
![]() ;
;
![]() .
.
де
![]() – кутова швидкість миттєвого обертального
руху навколо осі
– кутова швидкість миттєвого обертального
руху навколо осі
![]() .
Для її визначення запишемо співвідношення,
які одержуються з (5.8) та (5.9):
.
Для її визначення запишемо співвідношення,
які одержуються з (5.8) та (5.9):
 ;
;
![]() .
.
На підставі цих співвідношень знаходимо
(5.10)![]()
![]() .
.
Отже,
якщо тіло здійснює два незалежні
напрямлені в один бік обертальні рухи
навколо паралельних осей, то його
результуючий рух буде миттєвим обертальним
навколо миттєвої осі, яка паралельна
даним. Кутова швидкість результуючого
руху і положення точки
![]() ,
яка визначає миттєву вісь обертання,
знаходяться із співвідношень (5.10).
,
яка визначає миттєву вісь обертання,
знаходяться із співвідношень (5.10).
З плином
часу миттєва вісь обертання
![]() буде змінювати своє положення, описуючи
циліндричну поверхню.
буде змінювати своє положення, описуючи
циліндричну поверхню.
Обертання
напрямлені в протилежні боки.  Нехай
кутові швидкості
Нехай
кутові швидкості
![]() мають протилежні напрямки і припустимо,
що
мають протилежні напрямки і припустимо,
що
![]() .
Зобразимо як і в попередньому випадку,
переріз
.
Зобразимо як і в попередньому випадку,
переріз
![]() тіла (рис.
5.6).
тіла (рис.
5.6).
Швидкості
точок
![]() визначаємо з тих же міркувань, що і в
попередній задачі
визначаємо з тих же міркувань, що і в
попередній задачі
![]() ;
;
![]() .
.
Побудову
МЦШ (точка
![]() )
показано на
рис. 5.6. Тоді миттєва вісь
обертання проходить через точку
)
показано на
рис. 5.6. Тоді миттєва вісь
обертання проходить через точку
![]() ,
причому
,
причому
![]() ,
,
а
Рис.
5.6. Додавання двох
різнонапрямлених обертальних рухів
навколо паралельних осей
![]() .
.
Підставляючи
в ці рівності значення
![]() знаходимо остаточно
знаходимо остаточно
(5.11)![]()
![]() .
.
В
розглядуваному випадку результуючим
рухом є миттєвий обертальний рух навколо
осі
![]() ,
яка проходить через точку
,
яка проходить через точку
![]() .
Кутова швидкість цього руху і положення
миттєвої осі обертання визначається
із співвідношень (5.11). Одержані арезультати
показують, що вектори кутових швидкостей
при обертанні навколо паралельних осей
додаються так само як і вектори паралельних
сил.
.
Кутова швидкість цього руху і положення
миттєвої осі обертання визначається
із співвідношень (5.11). Одержані арезультати
показують, що вектори кутових швидкостей
при обертанні навколо паралельних осей
додаються так само як і вектори паралельних
сил.
Пара обертань.
Розглянемо випадок
![]() .
Така сукупність обертальних рухів
називається парою обертань. На підставі
формул (5.11) маємо
.
Така сукупність обертальних рухів
називається парою обертань. На підставі
формул (5.11) маємо
![]() ;
;
![]() .
.
Це
означає, що миттєвий центр швидкостей
(точка
![]() )
віднесена в нескінченність, а всі точки
тіла в даний момент мають однакові
швидкості. Таким чином, результуючим
рухом буде поступальний (або миттєвий
поступальний) з швидкістю
)
віднесена в нескінченність, а всі точки
тіла в даний момент мають однакові
швидкості. Таким чином, результуючим
рухом буде поступальний (або миттєвий
поступальний) з швидкістю
![]() ,
величина якої дорівнює
,
величина якої дорівнює
![]() ,
напрямленої перпендикулярно до площини
векторів
,
напрямленої перпендикулярно до площини
векторів
![]() .
Напрямок вектора
.
Напрямок вектора
![]() визначається за правилом гвинта.
визначається за правилом гвинта.
Таким
чином пара обертань еквівалентна
поступальному (або миттєвому поступальному
) руху з швидкістю
![]() ,
яка дорівнює моменту пари кутових
швидкостей цих обертань.
,
яка дорівнює моменту пари кутових
швидкостей цих обертань.
5.2.4.
Додавання обертального і поступального
рухів.
Розглянемо складний рух твердого тіла,
складовими якого є поступальний та
обертальний навколо нерухомої осі.
Відносним рухом будемо вважати обертання
навколо нерухомої осі
![]() з кутовою швидкістю
з кутовою швидкістю
![]() ,
а переносним – поступальний рух із
швидкістю
,
а переносним – поступальний рух із
швидкістю
![]() .
.
В залежності від кута між векторами
залежності від кута між векторами
![]() та
та
![]() можливі декілька випадків.
можливі декілька випадків.
1.
Швидкість поступального руху
перпендикулярна до осі обертання (![]() ).
На підставі теореми Ейлера (п. 4.2) такий
рух є плоскопаралельним, а отже миттєвим
обертальним навколо осі, яка паралельна
).
На підставі теореми Ейлера (п. 4.2) такий
рух є плоскопаралельним, а отже миттєвим
обертальним навколо осі, яка паралельна
![]() і проходить через МЦШ.
і проходить через МЦШ.
