
- •Числовые последовательности
- •Способы задания последовательностей
- •Свойства числовой последовательности
- •Рекуррентной формулой вида
- •Аналитической формулой вида
- •Свойства сходящихся последовательностей
- •Предел функции
- •Обозначение
- •Вычисление предела функции при приближении к точке
- •Пределы некоторых функций при приближении к точке:
- •С Лурки про предел
- •Приращение аргумента. Приращение функции
- •Экстремумы
- •Касательная к графику функции
- •Свойства касательной к графику функции Монотонность
- •Экстремумы
Касательная к графику функции
Касательная к графику любой функции в
некоторой точке
 – это всегда линейная функция вида
– это всегда линейная функция вида
 .
Она параллельна графику функции в данной
точке.
.
Она параллельна графику функции в данной
точке.
|
Свойство
производной: производная
|
|
Возьмем
некоторую точку
Нахождение касательной к графику любой функции
|
|
Свойства касательной к графику функции Монотонность
|
|
Рассмотрим возрастающую
функцию. Очевидно, что касательная к
возрастающему участку функции всегда
пересекает ось
Итак: Если
|
|
|
Рассмотрим убывающую
функцию. Очевидно, что касательная к
убывающему участку функции всегда
пересекает ось
Итак: Если
|
|
|
Если
|
В любом случае, при исследовании функции с помощью производной на монотонность, следует убедиться, что производная в данной точке существует и она конечна.
Экстремумы
Если функция
 имеет экстремум
в точке
имеет экстремум
в точке
 ,
то в этой точке производная
или равна нулю,
или не существует, но не
наоборот. При этом те точки, в которых
производная обращается в ноль,
называют стационарными,
а точки, где производная не
существует, называют
критическими.
,
то в этой точке производная
или равна нулю,
или не существует, но не
наоборот. При этом те точки, в которых
производная обращается в ноль,
называют стационарными,
а точки, где производная не
существует, называют
критическими.
Очевидно также, что если на некотором
участке функция сначала возрастает
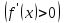 ,
затем в некоторой точке имеет
стационарную или критическую точку
,
затем в некоторой точке имеет
стационарную или критическую точку
 ,
после чего начинает убывать
,
после чего начинает убывать
 ,
то в этой точке мы имеем точку
максимума
функции. То же, только наоборот для точки
минимума. При этом функция
должна быть
непрерывна на рассматриваемом
промежутке.
,
то в этой точке мы имеем точку
максимума
функции. То же, только наоборот для точки
минимума. При этом функция
должна быть
непрерывна на рассматриваемом
промежутке.
Очевидно также, что максимум функции, если он существует, совпадает с одной из точек максимума.
Первообразная и интеграл
Процесс нахождения функции по ее производной называют интегрированием.
Функция
 ,
из которой получают производную
,
из которой получают производную
 называют первообразной.
называют первообразной.
Определение: функцию
 называют первообразной для функции
называют первообразной для функции
 ,
если при всех значениях выполняется
тождество
,
если при всех значениях выполняется
тождество
 .
.
Для любой функции
 существует неограниченно большое
количество первообразных вида
существует неограниченно большое
количество первообразных вида
 ,
т.к. производная константы – ноль.
,
т.к. производная константы – ноль.
Интеграл
Если функция
 имеет на промежутке
имеет на промежутке
 первообразную
первообразную
 ,
то множество всех первообразных, т.е.
множество функций вида
,
то множество всех первообразных, т.е.
множество функций вида
 ,
называют неопределенным
интегралом от функции
,
называют неопределенным
интегралом от функции
 и обозначают
и обозначают
 .
.
Правила нахождения первообразных
-
Интеграл суммы равны сумме интегралов

-
Постоянный множитель может быть вынесен за знак интеграла

-
Справедлива формула:

Формулы производных
-

-

-

-
 :
:

-

-
 :
:

-

-

-

-
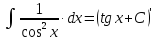
-

Определенный интеграл
Это интеграл вида
 ,
который по формуле Ньютона-Лейбница
раскладывается следующим образом (если
функция
,
который по формуле Ньютона-Лейбница
раскладывается следующим образом (если
функция
 непрерывна на данном участке):
непрерывна на данном участке):
 ,
где
,
где
 первообразная
для
первообразная
для
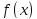 .
.
Определенный интеграл обладает всеми свойствами неопределенного интеграла.
Применение определенного интеграла
|
Если на участке
Определенный интеграл может также быть представлен как сумма прямоугольников вписывающихся в график функции, количество которых стремится к бесконечности, а ширина, соответственно, к нулю. |
|

 функции
функции
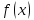 находит угловой коэффициент касательной
в точке
находит угловой коэффициент касательной
в точке
 .
В этом геометрический смысл
производной.
.
В этом геометрический смысл
производной. ,
тогда:
,
тогда: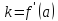 (свойство производной)
(свойство производной)


 ,
имеем
,
имеем

 и вычислить
и вычислить

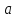 ,
,
 и
и
 в формулу:
в формулу:


 под углом [0,90], образуя угол первой
четверти. А значит, тангенс этого угла
(т.е. угловой
коэффициент) в таком случае
больше или
равен нулю.
под углом [0,90], образуя угол первой
четверти. А значит, тангенс этого угла
(т.е. угловой
коэффициент) в таком случае
больше или
равен нулю. ,
то
,
то


 под углом [90,180], образуя угол второй
четверти. А значит, тангенс этого угла
(т.е. угловой
коэффициент) в таком случае
меньше или
равен нулю.
под углом [90,180], образуя угол второй
четверти. А значит, тангенс этого угла
(т.е. угловой
коэффициент) в таком случае
меньше или
равен нулю. ,
то
,
то

 ,
то
,
то
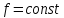
 непрерывная на
этом участке функция
непрерывная на
этом участке функция
 принимает только
неотрицательные значения, то
выражение
принимает только
неотрицательные значения, то
выражение
 находит площадь
криволинейной трапеции,
образованной осью x
снизу, графиком функции
находит площадь
криволинейной трапеции,
образованной осью x
снизу, графиком функции
 сверху и числами
сверху и числами
 и
и
 по бокам.
по бокам.