
- •Числовые последовательности
- •Способы задания последовательностей
- •Свойства числовой последовательности
- •Рекуррентной формулой вида
- •Аналитической формулой вида
- •Свойства сходящихся последовательностей
- •Предел функции
- •Обозначение
- •Вычисление предела функции при приближении к точке
- •Пределы некоторых функций при приближении к точке:
- •С Лурки про предел
- •Приращение аргумента. Приращение функции
- •Экстремумы
- •Касательная к графику функции
- •Свойства касательной к графику функции Монотонность
- •Экстремумы
Вычисление предела функции при приближении к точке
Ученые доказали, что если выражение составлено
из рациональных и иррациональных (и как
следствие, тригонометрических) выражений,
то функция
составлено
из рациональных и иррациональных (и как
следствие, тригонометрических) выражений,
то функция
 непрерывна
на любом участке, где она определена.
непрерывна
на любом участке, где она определена.
А если функция непрерывна,
то и монотонна. Значит, выражение
непрерывна,
то и монотонна. Значит, выражение в этом случае тождественно. Т.о. если
выражение
в этом случае тождественно. Т.о. если
выражение составлено
из рациональных и иррациональных
выражений, то для любого
составлено
из рациональных и иррациональных
выражений, то для любого
 требуется
выяснить, определена ли функция в этой
точке и если определена, топредел функции
в этой точке будет равен значению функции
в этой же точке:
требуется
выяснить, определена ли функция в этой
точке и если определена, топредел функции
в этой точке будет равен значению функции
в этой же точке:
 .
.
Пределы некоторых функций при приближении к точке:
С Лурки про предел
Возьмём sin(x)/x. Подставим вместо икса ноль— получим ноль делить на ноль. Мы с начальных классов знаем, что нельзя делить на ноль.
Давай подставим 1 (в радианах). Калькулятор даёт: 0,8414709848078965066525023216303
Теперь подставим 0.1. Калькулятор даёт: 0,99833416646828152306814198410622
Давай ещё приблизимся к нулю и подставим 0.01. Получим sin(0.01)/0.01 = 0,99998333341666646825424382690997
Наверное, уже понятно что, приближаясь по иксу к нулю, мы получим по игреку всё ближе к единице. Хотя в самом нуле выражение sin(x)/x не имеет смысла (нельзя делить на ноль), говорят, что его предел при приближении к нулю равен единице.
Приращение аргумента. Приращение функции
Пусть функция определена
в точках
определена
в точках
 и
и
 .
При переходе от точки
.
При переходе от точки
 к
точке
к
точке
 ,
разность
,
разность
 называется
приращением аргумента
называется
приращением аргумента
 ,
а разность
,
а разность
 называется приращением функции
называется приращением функции
 .
.
Найдем
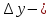 приращение функции при переходе от
аргумента
приращение функции при переходе от
аргумента
 каргументу
каргументу
 :
:


По определению непрерывности функции
в точке
 :
:


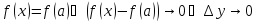
Отсюда вывод: функция
 непрерывна в точке
непрерывна в точке
 ,
если в точке
,
если в точке
 выполняется условие: при
выполняется условие: при
 ,
то
,
то

Пример:
-
Найдем приращение
 функции
функции
 ,
подставив в аргумент значение
,
подставив в аргумент значение
 :
:


-
Предел отношения приращения функции к пределу аргумента при
 ,
т.е.
,
т.е.
 :
:

Примечание: если в ответе под знаком
предела имеется
 ,
топри
,
топри он может быть заменен на
он может быть заменен на
 ©byКО.
©byКО.
Производная и дифференцирование
Процесс нахождения производной функции называют дифференцированием.

Где
 означает «предел существует и он
конечен».
означает «предел существует и он
конечен».
Правила дифференцирования
Общие правила


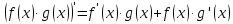

Формулы
-
 :
C – const
:
C – const -
 :
:

Частные случаи:
-
 ,
пример применения:
,
пример применения:

-
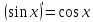
-

-

-

-

-
…
Применение производной в исследовании функции
Угловой коэффициент
Y
|
Угловой коэффициент прямой – коэффициент
Свойства углового коэффициента:
( При этом
|
X 




b |
Экстремумы
|
|
Экстремум – значение минимума или максимума в точке, наибольшее или наименьшее значение функции в локальном смысле, максимум или минимум участка функции.
Точку
Точку
|




 в формуле прямой
в формуле прямой
 .
Численно составляет тангенс
(меньшего) угла между положительным
направлением оси абсцисс и данной
линией.
.
Численно составляет тангенс
(меньшего) угла между положительным
направлением оси абсцисс и данной
линией.
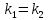
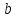 – значение от
– значение от
 ,
т.е. точка пересечения ординаты )
,
т.е. точка пересечения ординаты )



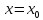 называют точкой
максимума, если существует
некоторая окрестность, для всех точек
которой, кроме самой точки
называют точкой
максимума, если существует
некоторая окрестность, для всех точек
которой, кроме самой точки
 выполняется условие
выполняется условие
 .
.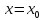 называют точкой
минимума, если существует
некоторая окрестность, для всех точек
которой, кроме самой точки
называют точкой
минимума, если существует
некоторая окрестность, для всех точек
которой, кроме самой точки
 выполняется условие
выполняется условие
 .
.