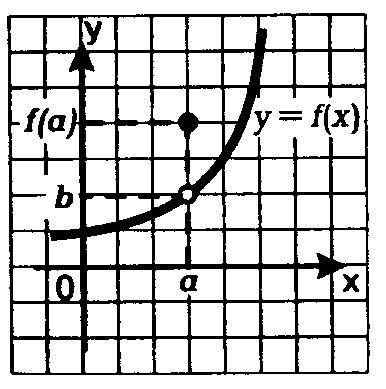- •Числовые последовательности
- •Способы задания последовательностей
- •Свойства числовой последовательности
- •Рекуррентной формулой вида
- •Аналитической формулой вида
- •Свойства сходящихся последовательностей
- •Предел функции
- •Обозначение
- •Вычисление предела функции при приближении к точке
- •Пределы некоторых функций при приближении к точке:
- •С Лурки про предел
- •Приращение аргумента. Приращение функции
- •Экстремумы
- •Касательная к графику функции
- •Свойства касательной к графику функции Монотонность
- •Экстремумы
Числовые последовательности
Числоваяпоследовательность
– это функция натурального аргумента,
т.е.
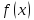 ,
где
,
где
 .
Т.о. каждому натуральному числу 1,2,3,4,…
соответствует определенное значение
функции. Обозначается
.
Т.о. каждому натуральному числу 1,2,3,4,…
соответствует определенное значение
функции. Обозначается
 .
.
Способы задания последовательностей
-
Устно, перечислением первых нескольких элементов
-
Аналитически – формулой n-го члена
-
Рекуррентно – формулой, позволяющей вычислить n-й член последовательности, по известным предыдущимэлементам последовательности.
Свойства числовой последовательности
Т.к. числовая последовательность – это частный случай функции, она обладает некоторыми свойствами функций.
-
Ограниченность
-
ЧПограниченасверху –
 или
или

-
ЧП ограниченаснизу –
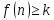 или
или

-
ЧП ограничена – ЧПограничена и снизу и сверху
-
-
Монотонность
-
Монотонная ЧП – ЧП возрастающая или убывающая
-
Возрастающая ЧП – Еслидля любых
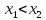 выполняется
выполняется

-
Убывающая ЧП – Еслидля любых
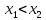 выполняется
выполняется
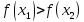
-
Частные случаи числовых прогрессий
Арифметическая прогрессия
Арифметическая прогрессия – это разновидность числовой последовательности, заданная:
-
Рекуррентной формулой вида
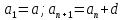
-
Аналитической формулой вида
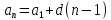
Сумма первых
 членов арифметической прогрессии:
членов арифметической прогрессии:
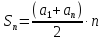
Геометрическая прогрессия
Геометрическая прогрессия – это разновидность числовой последовательности, заданная:
-
Рекуррентной формулой вида
-
Аналитической формулой вида
Сумма первых
 членов геометрической прогрессии:
членов геометрической прогрессии: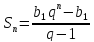 ,
где
,
где
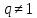
Геометрическая
прогрессия при
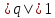
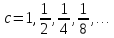 ;
;
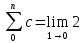
Сумма бесконечной геометрической
прогрессии при
 равна:
равна:
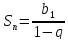
Пример:

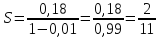
Ответ:

Предел числовой последовательности
|
Пусть
Тогда
интервал
|
|
|
Число
Обозначение:
Если последовательность не имеет предела, то она расходится. Графически,
прямая
|
|
Свойства сходящихся последовательностей
-
Если последовательность сходится, то только к одному пределу.
-
Если последовательность сходится, то она ограниченна.
-
Если последовательность монотонна и ограниченна, то она сходится.
Предел функции
Смысл предела функции тот же (при
 ,
,
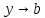 ),
что и для предела последовательности,
но аргумент функции, в отличие от
аргумента последовательности, может
принимать отрицательные значения, что
позволяет функции сходиться к двум
пределам.
),
что и для предела последовательности,
но аргумент функции, в отличие от
аргумента последовательности, может
принимать отрицательные значения, что
позволяет функции сходиться к двум
пределам.
Обозначение
|
Если прямая
|
|
|
Если прямая
|
|
|
Если прямая
|
|
Правилавычисления пределов функций
Пределы некоторых видов функций
Приемы вычисления пределов функций
Для решения выражений вида
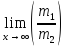 ,
где
,
где
 и
и
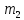 –
многочлены применяют прием: делят и
числитель и знаменатель дроби почленно
на наивысшую степень переменной
–
многочлены применяют прием: делят и
числитель и знаменатель дроби почленно
на наивысшую степень переменной
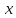 из
имеющихся.
из
имеющихся.
Пример:
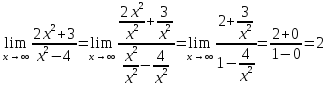
Предел функции при
приближении к точке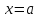
Предел функции при
приближении к точке
при
приближении к точке
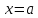 на
монотонном участке равен тому числу,
которое должна принимать функция
на
монотонном участке равен тому числу,
которое должна принимать функция
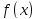 в
точке
в
точке
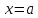 для поддержания монотонности в этой
точке. Т.е. для поддержания монотонности
приращения
для поддержания монотонности в этой
точке. Т.е. для поддержания монотонности
приращения
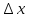 и
соответствующего
и
соответствующего
 .
.
Данное значение не имеет ни какого
отношения к тому, как функция ведет себя
в точке
 на
самом деле.
на
самом деле.
Приближенное значение
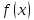 при приближении к пределу
при приближении к пределу
Из определения (т.к. данный участок
монотонен) следует, что если
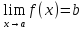 ,
то в достаточно малой окрестности точки
,
то в достаточно малой окрестности точки
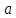 выполняется приближенное равенство
выполняется приближенное равенство
 и чемближе
и чемближе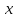 к
к ,
тем ближе значение
,
тем ближе значение к
числу
к
числу
 .
При этом сама точка aисключается
из рассмотрения.
.
При этом сама точка aисключается
из рассмотрения.
Непрерывность функции в точке
Функция непрерывна в точке a,
если в данной точке она определена,
монотонна и ее значение совпадает с
ожидаемым значением, вычисленным на
основе монотонности, т.е.
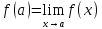 .
На графике это отражается в отсутствии
«проколов» в функции и ее плавном
изменении без «скачков».
.
На графике это отражается в отсутствии
«проколов» в функции и ее плавном
изменении без «скачков».
|
Пример: На рисунке предел функции в точке a равен b, т.к. именно это значение должна принимать функция для поддержания монотонности участка.На самом же деле функция принимает в этой точке иное значение и потому в этой точке она не монотонна.
А т.к. в этой
точке она не монотонна, хотя и определена,
то функция имеет «прокол» в точке
|
|
Более полный пример:
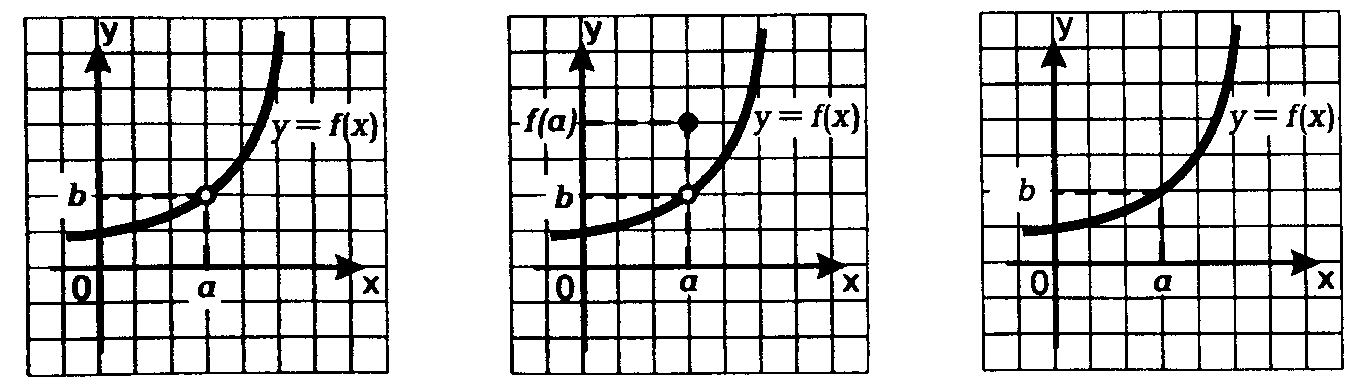
Рисункам соответствуют три варианта поведения функции в точке a:
-
Первая функция не принимает значения в точке
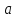 и
потому не является непрерывной в этой
точке. На графике это отражено в том,
что функция имеет «прокол» в точке a.
и
потому не является непрерывной в этой
точке. На графике это отражено в том,
что функция имеет «прокол» в точке a. -
Вторая функция принимает значение bв точке
 ,
но оно не совпадает со
значением
,
но оно не совпадает со
значением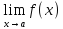 ,
из чего следует, что в этой точке функция
не монотонна.
Следовательно, она не является непрерывной
в точке a. На графике
это отражено в том, что функция имеет
«скачок» в точке a.
,
из чего следует, что в этой точке функция
не монотонна.
Следовательно, она не является непрерывной
в точке a. На графике
это отражено в том, что функция имеет
«скачок» в точке a. -
Третья функция принимает значение bв точке
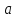 ,
ионо совпадает со значением
,
ионо совпадает со значением
 .
Значит, функция непрерывна в точке a.
.
Значит, функция непрерывна в точке a.
Функция непрерывна на промежутке ,
если она непрерывна в каждой точке
промежутка.
,
если она непрерывна в каждой точке
промежутка.

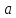 – точка на прямой, а
– точка на прямой, а
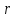 – положительное число.
– положительное число.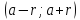 называют окрестностью
точки
называют окрестностью
точки ,
а число
,
а число
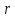 – радиусом окрестности.
– радиусом окрестности.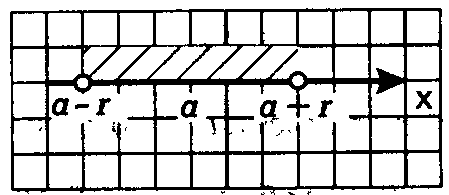
 называют
пределом
последовательности
называют
пределом
последовательности
 ,
если в любой заранее выбранной
окрестности этой точки содержатся
все члены последовательности, начиная
с некоторого номера. При этомвыполняется
приближенное равенство
,
если в любой заранее выбранной
окрестности этой точки содержатся
все члены последовательности, начиная
с некоторого номера. При этомвыполняется
приближенное равенство
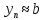 и чем больше
и чем больше
 ,
тем ближе значение
,
тем ближе значение
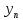 к
числу
к
числу
 ,
хотя самого числа bоно
никогда не достигает.
,
хотя самого числа bоно
никогда не достигает.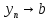
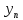 сходитсяк
сходитсяк »
»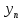 стремитсяк
стремитсяк »
»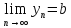
 при стремлении
при стремлении кбесконечности равен
кбесконечности равен
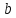 »
» равен
равен
 »
»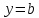 являетсягоризонтальной
асимптотойграфика функции
являетсягоризонтальной
асимптотойграфика функции
 .
.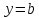 является
горизонтальной асимптотой графика
функции
является
горизонтальной асимптотой графика
функции
 при
при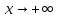 ,
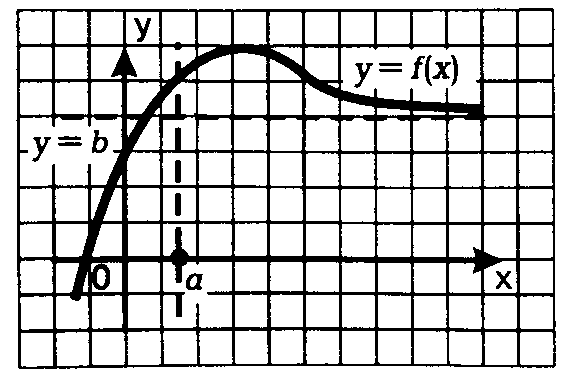
тоэто обозначается
,
тоэто обозначается
 .
.
 является
горизонтальной асимптотой графика
функции
является
горизонтальной асимптотой графика
функции
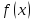 при
при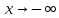 ,
тоэто обозначается
,
тоэто обозначается
 .
.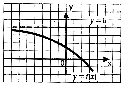
 является
горизонтальной асимптотой графика
функции
является
горизонтальной асимптотой графика
функции
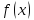 как при
как при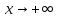 ,
таки при
,
таки при
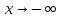 ,
тоэто обозначается
,
тоэто обозначается
 или
или
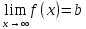 .
.

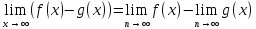

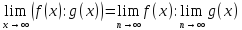

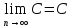

 и
потому не является непрерывной в этой
точке.
и
потому не является непрерывной в этой
точке.