
- •Лекція 5 Тема: Векторні простори. Алгебри
- •2. Поняття, приклади і найпростіші властивості векторного простору
- •3. Лінійна залежність системи векторів. Базис і розмірність векторного простору Означення. Лінійною комбінацією векторів векторного простору називається вектор вигляду
- •4. Координати вектора у векторному просторі. Розкладання вектора за базисом
- •2) Розкладемо вектор за базисом :
- •Розв’язуючи цю систему будь-яким способом, знайдемо
- •4. Векторні простори із скалярним добутком
- •5. Підпростори векторного простору
- •6. Лінійний оператор та його матриця
- •6. Поняття алгебри. Приклади алгебр
- •8. Ізоморфізм та гомоморфізм алгебр
5. Підпростори векторного простору
Означення.
Непорожня
підмножина
![]() векторного простору
векторного простору
![]() називається
підпростором
простору
називається
підпростором
простору
![]() ,
якщо воно є векторним простором відносно
операцій, визначених в
,
якщо воно є векторним простором відносно
операцій, визначених в
![]() .
.
Це
означає, що множина
![]() задовольняє аксіомам векторного
простору, якщо додавати його елементи
і множити їх на числа з поля
задовольняє аксіомам векторного
простору, якщо додавати його елементи
і множити їх на числа з поля
![]() (над яким заданий векторний простір
(над яким заданий векторний простір
![]() )
так, як це визначено для елементів
простору
)
так, як це визначено для елементів
простору
![]() .
.
Теорема
(критерій підпростору). Непорожня
підмножина
![]() векторного простору
векторного простору
![]() є
підпростором простору
є
підпростором простору
![]() оді і тільки тоді, коли виконується
наступні умови:
оді і тільки тоді, коли виконується
наступні умови:
-
Якщо
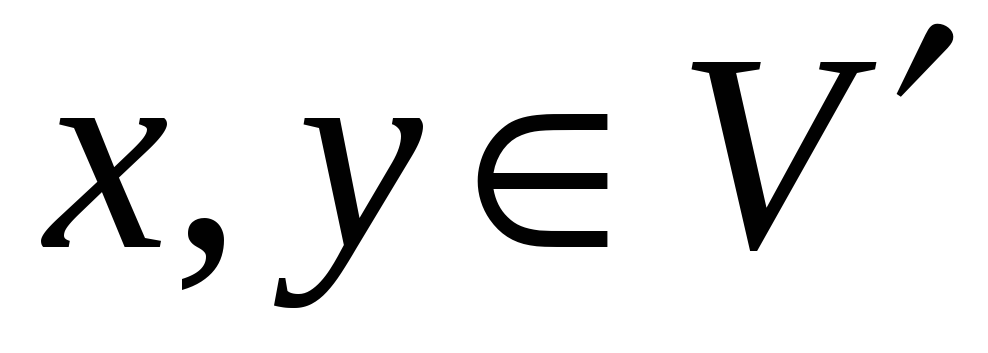 ,
то
,
то
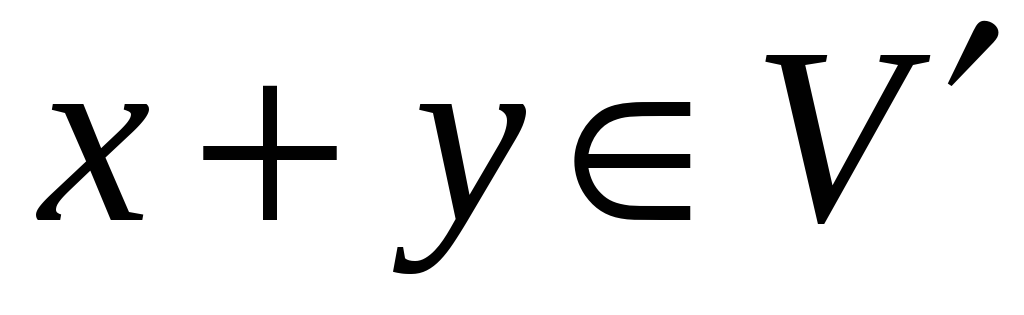 ;
; -
Якщо
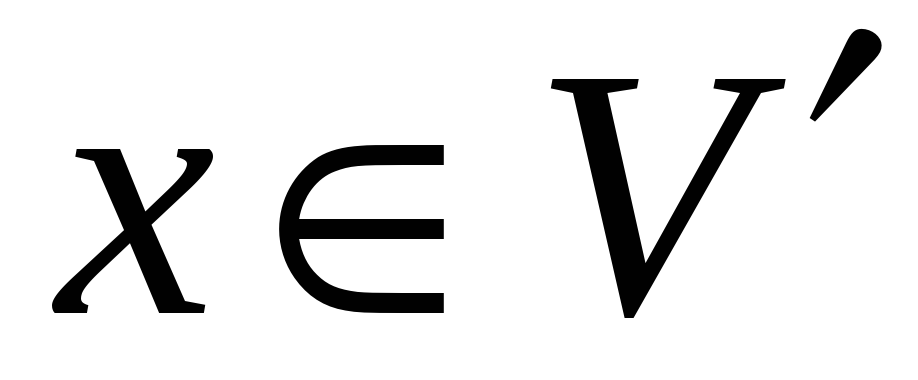 ,
,
 то
то
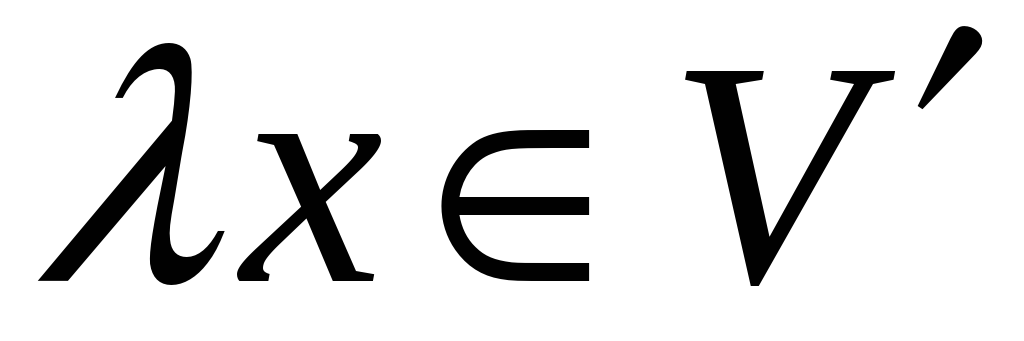 .
.
Кожний підпростір будь-якого векторного простору саме по собі є векторним простором. тому всі поняття, які були введені для просторів (розмірність, базис та ін.) розповсюджуються і на підпростори.
Теорема (про розмірність підпростору). Розмірність будь-якого підпростору векторного простору не більше розмірності простору.
Приклади підпросторів.
1) Множина
![]() ,
яка містить тільки нульовий елемент
,
яка містить тільки нульовий елемент
![]() є підпростором будь-якого векторного
простору. Його називають нульовим
підпростором.
В нульовому підпросторі нема лінійно
незалежних систем векторів. Його базис
– порожня множина. Його розмірність
вважають нульовою.
є підпростором будь-якого векторного
простору. Його називають нульовим
підпростором.
В нульовому підпросторі нема лінійно
незалежних систем векторів. Його базис
– порожня множина. Його розмірність
вважають нульовою.
2)
Будь-який векторний простір
![]() є своїм підпростором.
є своїм підпростором.
Нульовий
підпростір
![]() і сам простір
і сам простір
![]() звичайно називають невласними
підпросторами.
звичайно називають невласними
підпросторами.
3) В
арифметичному числовому векторному
просторі
![]() множина
множина
![]() ,
,
![]() ,
векторів вигляду
,
векторів вигляду
![]() є підпростором.
є підпростором.
4)
Векторний простір многочленів з
коефіцієнтами з поля
![]() є підпростором векторного простору
функцій, неперервних на відрізку
є підпростором векторного простору
функцій, неперервних на відрізку
![]() ,
якщо многочлени вважати заданими на
відрізку
,
якщо многочлени вважати заданими на
відрізку
![]() .
.
5) У
векторному просторі
![]() геометричних векторів підпросторами
будуть вусі площини і всі прямі, що
проходять через початок координат.
геометричних векторів підпросторами
будуть вусі площини і всі прямі, що
проходять через початок координат.
6) Лінійні
оболонки є цікавим прикладом підпростору.
Нехай
![]() – довільна система векторів простору
– довільна система векторів простору
![]() .
Множина всіх векторів, які є лінійними
комбінаціями векторів системи
.
Множина всіх векторів, які є лінійними
комбінаціями векторів системи
![]() є підпростором простору
є підпростором простору
![]() ,
який позначається
,
який позначається
![]() і називається лінійною оболонкою
векторів
і називається лінійною оболонкою
векторів
![]() ,
або підпростором, натягнутим на вектори
,
або підпростором, натягнутим на вектори
![]() .
.
6. Лінійний оператор та його матриця
Означення.
Лінйним
оператором
у векторному просторі
![]() називається відображення векторного
простору
називається відображення векторного
простору
![]() в себе
в себе
![]()
![]() →
→![]() таке, що виконані наступні умови (умови
лінійності):
таке, що виконані наступні умови (умови
лінійності):
1)
![]()
![]()
![]() ;
;
1)
![]()
![]()
![]()
![]() ;
;
Лінійний оператор
називається також лінійним перетворенням
векторного простору
![]() .
Лінійні перетворення є гомоморфізмами.
.
Лінійні перетворення є гомоморфізмами.
З означення безпосередньо випливають наступні
Найпростіші властивості лінійного оператору:
1) Образом нуль-вектора
є нуль-вектор:
![]() .
.
2) Образом вектора,
протилежного довільному вектору
![]()
![]() є вектор, протилежний образу вектора
є вектор, протилежний образу вектора
![]() :
:
![]()
3) Образом лінійної
комбінації довільних векторів
![]() простору
простору
![]() є лінійна комбінація (з тими ж коефіцієнтами)
образів цих векторів:
є лінійна комбінація (з тими ж коефіцієнтами)
образів цих векторів:
![]()
Приклади лінійних операторів:
1)
![]()
![]() →
→![]() :
:![]() – нульовий оператор. Позначається
– нульовий оператор. Позначається
![]() .
.
2)
![]()
![]() →
→![]() :
:![]() – тотожний (одиничний) оператор.
Позначається
– тотожний (одиничний) оператор.
Позначається
![]() .
.
3)
![]()
![]() →
→![]() – поворот площини навколо початку
координат на кут
– поворот площини навколо початку
координат на кут
![]() в додатному напрямку.
в додатному напрямку.
4)
![]()
![]() →
→![]() – ортогональне проектування векторів
на деяку площину.
– ортогональне проектування векторів
на деяку площину.
5) Нехай
![]() – векторний простір функцій,
диференційованих на всій числовій
прямій. Розглянемо перетворення
– векторний простір функцій,
диференційованих на всій числовій
прямій. Розглянемо перетворення
![]() простору
простору
![]() ,
яке кожній функції
,
яке кожній функції
![]()
![]() ставить у відповідність її похідну,
тобто
ставить у відповідність її похідну,
тобто
![]() .
За властивостями похідної 1)
.
За властивостями похідної 1)
![]() і
і
2)
![]() .
.
Таким чином,
диференціювання – лінійний оператор
в
![]() .
.
6) Нехай
![]()
![]() – векторний простір числових рядків,
– векторний простір числових рядків,
![]() – матриця порядку
– матриця порядку
![]() з дійсними елементами. Перетворення
простору
з дійсними елементами. Перетворення
простору
![]()
![]() ,
яке кожному вектору
,
яке кожному вектору
![]() ставить у відповідність вектор
ставить у відповідність вектор
![]() ,
координати якого визначаються за
формулою
,
координати якого визначаються за
формулою
![]() ,
тобто
,
тобто
![]() є лінійним оператором.
є лінійним оператором.
Нехай у векторному
просторі
![]() заданий деякий базис
заданий деякий базис
![]() .
.
Означення.
Матрицею
лінійного оператора
![]() в базисі
в базисі
![]() називається матриця
називається матриця
 ,
,
елементами якої
є коефіцієнти в розкладі образів векторів
![]() за базисом
за базисом
![]() ,
тобто
,
тобто
![]() ;
;
![]() ;
;
………………………………………..
![]() .
.
З означення
випливає, що стовпцями матриці
![]() є координатні рядки векторів
є координатні рядки векторів
![]() ,
,
![]() ,
в базисі
,
в базисі
![]() .
.
Приклади.
1) Матрицею тотожного
оператора є одинична матриця:
![]() ,
,
2) Матрицею нульового
оператора є нульова матриця
![]() .
.
При фіксованому
базисі
![]() кожному лінійному оператору
кожному лінійному оператору
![]() простору
простору
![]() відповідає певна матриця
відповідає певна матриця
![]() -го
порядку – матриця цього лінійного
оператора
-го
порядку – матриця цього лінійного
оператора
![]() .
Справедливе і обернене: кожна матриця
.
Справедливе і обернене: кожна матриця
![]() -го
порядку є матрицею певного лінійного
оператора простору
-го
порядку є матрицею певного лінійного
оператора простору
![]() в базисі
в базисі
![]() .
.
У координатному
вигляді дія лінійного оператора
![]() на вектор
на вектор
![]()
![]() зводиться до множення матриці лінійного
оператора
зводиться до множення матриці лінійного
оператора
![]() на координатний стовпчик вектора
на координатний стовпчик вектора
![]() :
:
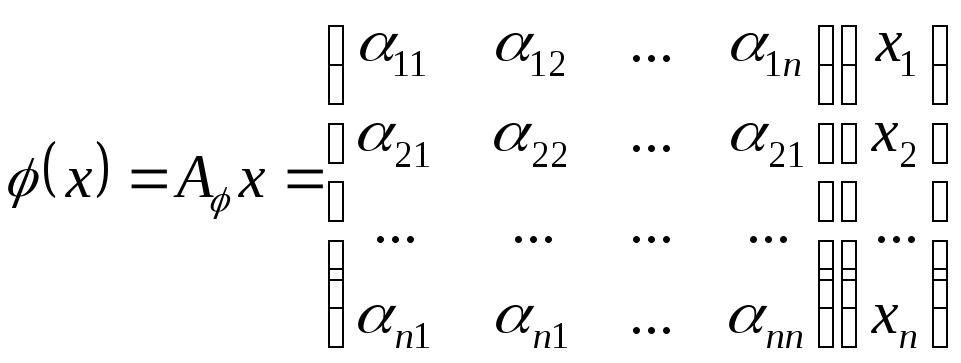 .
.
Ясно, що матриця
оператора
![]() залежить від вибору базису простору
залежить від вибору базису простору
![]() .
.
