Ю.Д.Жданова. Лекції з ВГПМ. М1 Прикладні аспекти ЛА. Лекція № 2

Лекція 2 Тема: Лінійні оператори в векторних просторах

План лекції:

1. Лінійні оператори в векторних просторах.

2. Лінійні оператори і матриці.

3. Дії з лінійними операторами.

4. Визначник матриці

4.1 Підстановки

4.2 Підстановочні матриці

4.3 Цикли, транспозиції

4.4 Визначник матриці

4.5 Подібні підстановки, задача Лагранжа

5. Характеристичний та мінімальний многочлени матриці.

6. Мінімальний многочлен вектора відносно матриці.

7. Власний, інваріантний і циклічний підпростори лінійного оператора.

1. Лінійні оператори

Нехай і – векторні простори над одним й тим самим полем .

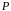Означення. Кажуть, що з простору в простір діє оператор 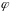(або відображення , перетворення , функція ), якщо кожному вектору за деяким правилом ставиться у відповідність вектор :

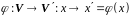
Вектор 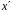називається образом вектора 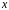, а вектор – прообразом вектора при відображенні .

Якщо простори і збігаються, то кажуть, що оператор діє в просторі .

Найпростішими є лінійні оператори.

Означення. Оператор називається лінійним оператором у векторному просторі , виконані наступні умови (умови лінійності):

1) ;

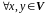
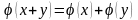2) .

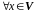
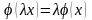Лінійний оператор називається також лінійним перетворенням векторного простору . Лінійні перетворення є гомоморфізмами.

З означення безпосередньо випливають наступні

Найпростіші властивості лінійного оператора:

1) Образом нуль-вектора є нуль-вектор: .

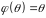2) Образом вектора, протилежного довільному вектору є вектор, протилежний образу вектора :

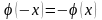
3) Образом лінійної комбінації довільних векто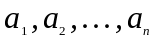рів простору є лінійна комбінація (з тими ж коефіцієнтами) образів цих векторів:

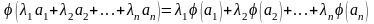
Приклади лінійних операторів:

1) 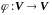: 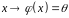– нульовий оператор. Позначається .

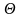2) :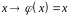 – тотожний (одиничний) оператор. Позначається .

3) :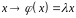 – оператор подібності.

4) 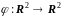– поворот площини навколо початку координат на кут в додатному напрямку.

5) – ортогональне проектування векторів на деяку площину.

6) Нехай 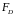– векторний простір функцій, диференційованих на всій числовій прямій. Розглянемо перетворення простору , яке кожній функції 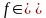ставить у відповідність її похідну, тобто 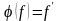. За властивостями похідної 1) 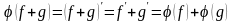і

2) .

Таким чином, диференціювання – лінійний оператор в .

7) Нехай 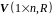– векторний простір числових рядків, 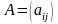– матриця порядку 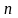з дійсними елементами. Перетворення простору , яке кожному вектору 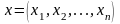ставить у відповідність вектор 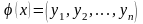, координати якого визначаються за формулою , тобто 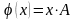є лінійним оператором.

Теорема. Нехай – лінійний оператор у векторному просторі , 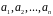– базис в . Тоді лінійний оператор однозначно визначається заданням образів 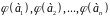векторів базису .

Приклад. Оператор переводить вектор 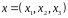в вектор 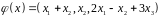. Показати, що оператор – лінійний.

Розв’язання. Перевіримо умови лінійності.

1. ;

, ,

, .

,

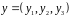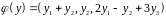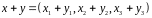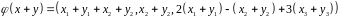
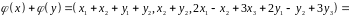
Бачимо, що .

2) ;

, ,

, ,

,

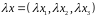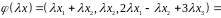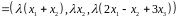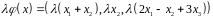
Бачимо, що .

Обидві умови лінійності виконані. Отже, оператор – лінійний.