
- •Лекція № 5 Тема: Розв’язування алгебраїчних конгруенцій
- •1. Розв’язування квадратних конгруенцій за простим модулем
- •7.2) Обчислити , .
- •7.2) Обчислимо , .
- •Алгоритм Шенкса -Тонеллі
- •2. Алгебраїчні конгруенції -го степеня за простим модулем та способи їх розв'язування
- •1. Заміна коефіцієнтів абсолютно найменшими лишками за модулем .
- •2.Зниження степеня конгруенції.
- •3. Перехід до еквівалентної конгруенції, старший коефіцієнт якої дорівнює 1.
- •3. Число розв’язків конгруенції -го степеня за простим модулем
- •4. Алгебраїчні конгруенції -го степеня за складеним модулем та способи їх розв'язування
- •5. Алгоритм Берлекемпа розкладання многочлена на незвідні множники над скінченним полем
- •Алгоритм Берлекемпа (Berlecamp’s Algorithm)
Ю.Д.Жданова. Лекції з ВГПМ. М2 ТЧ обчислювальні алгоритми. Лекція № 5
Лекція № 5 Тема: Розв’язування алгебраїчних конгруенцій
План лекції:
1. Розв’язування квадратних конгруенцій за простим модулем. Алгоритм Шенкса-Тонеллі.
2.
Алгебраїчні конгруенції
 -го
степеня за простим модулем та способи
їх розв'язування.
-го
степеня за простим модулем та способи
їх розв'язування.
3. Число розв’язків конгруенції -го степеня за простим модулем.
4. Алгебраїчні конгруенції -го степеня за складеним модулем та способи їх розв'язування.
5. Алгоритм Берлекемпа розкладання многочлена на незвідні множники над скінченним полем.
1. Розв’язування квадратних конгруенцій за простим модулем
Розглянемо
квадратну двочленну конгруенцію за
простим непарним модулем
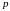 :
:
 ,
,
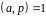 (1)
(1)
За допомогою очевидної заміни змінної до конгруенції (1) зводиться довільне рівняння
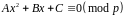 .
.
Число
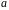 називається
квадратичним
лишком за модулем
,
якщо конгруенція (1) має розв’язки. Число
називається
квадратичним
нелишком
за модулем
,
якщо конгруенція (1) розв’язків не має.
називається
квадратичним
лишком за модулем
,
якщо конгруенція (1) має розв’язки. Число
називається
квадратичним
нелишком
за модулем
,
якщо конгруенція (1) розв’язків не має.
За
критерієм Ейлера для визначення
квадратичних лишків і нелишків., якщо
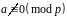 ,
то
конгруенція (1)
має розв’язки тоді і тільки тоді, коли
,
то
конгруенція (1)
має розв’язки тоді і тільки тоді, коли
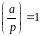 ,
тобто
,
тобто
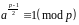 (2)
(2)
Готової формули для розв’язування алгебраїчних конгруенцій другого степеня не існує.
Відомі окремі випадки:
Якщо
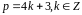 ,
то
,
то
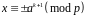 .
.Якщо
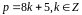 ,
то у випадку
,
то у випадку
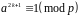 ,
а у випадку
,
а у випадку
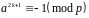
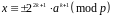 .
.
У
випадках
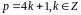 ,
,
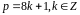 для розв’язування (1) застосовується
апроксимаційний
(наближувальний) алгоритм,
який полягає у наступному:
для розв’язування (1) застосовується
апроксимаційний
(наближувальний) алгоритм,
який полягає у наступному:
Обчислити значення символу Лежандра
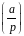 .
Якщо
.
Якщо
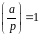 ,
–
квадратичний лишок, якщо
,
–
квадратичний лишок, якщо
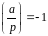 ,
квадратичний нелишок.
,
квадратичний нелишок.Записати число
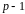 у вигляді добутку парного і непарного
чисел:
у вигляді добутку парного і непарного
чисел:
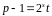 ,
,
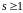 .
.Знайти випадковий квадратичний нелишок
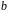 за модулем
за модулем
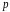 ,
тобто для
виконано співвідношення
,
тобто для
виконано співвідношення
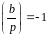 .
.Покласти
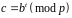 .
.Обчислити
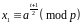 .
(
.
(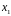 – наближене значення кореня конгруенції
).
– наближене значення кореня конгруенції
).
Квадратний
корінь з
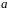 за модулем
шукати у вигляді
за модулем
шукати у вигляді
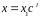 .
.
Знайти степінь
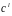 ,
,
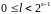 .
Щоб визначити число
.
Щоб визначити число
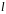 ,
,
запишемо його у двійковій системі
числення
,
,
запишемо його у двійковій системі
числення
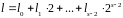 .
.
Визначити, які значення (0 або 1) набувають двійкові цифри
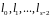 наступним чином:
наступним чином:
7.1)
Обчислити
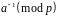 .
.
7.2) Обчислити , .
Покласти
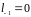 ,
,
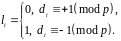 ,
.
,
.
Відповідь:
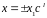 – квадратний корінь з
за модулем
.
– квадратний корінь з
за модулем
.
Приклад 1. Розв’язати конгруенцію:
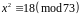
Розв’язання
Обчислимо значення символу Лежандра
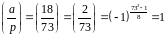
Отже, конгруенція має розв’язки.
Запишемо число у вигляді добутку парного і непарного чисел:
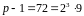 .
Отже,
.
Отже,
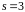 ,
,
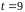 .
.
Знайдемо квадратичний нелишок за модулем
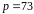 .
Нехай
.
Нехай
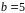 ,
тому що
,
тому що
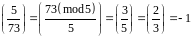 .
.
Покладемо
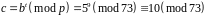
Обчислимо
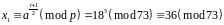
Квадратний корінь з 18 за модулем шукаємо у вигляді
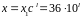
Знайдемо степінь ,
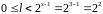 .
Щоб визначити число
,
.
Щоб визначити число
,
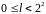 ,
запишемо його у двійковій системі
числення:
,
запишемо його у двійковій системі
числення:
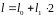
Визначимо, які значення (0 або 1) набувають двійкові цифри
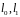 наступним чином:
наступним чином:
7.1)
Обчислимо
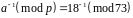 .
За розширеним алгоритмом Евкліда
визначимо:
.
За розширеним алгоритмом Евкліда
визначимо:
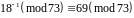 .
.
7.2) Обчислимо , .
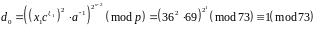
Значить,
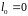 .
.
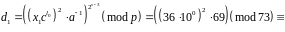
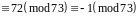
Значить,
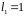 .
.
Отже,
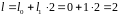 .
.
Шукані корені
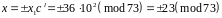 ,
,
або
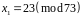 ,
,
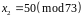 .
.
Перевірка:
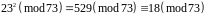 .
.
Алгоритм
Шенкса-Тонеллі (Shanks-Tonelli)
добування квадратного кореня є більш
ефективним, ніж апроксимаційний алгоритм,
у випадку, коли
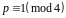 ,
або
,
або
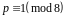 .
Збережемо позначення такі, як для
попереднього алгоритму.
.
Збережемо позначення такі, як для
попереднього алгоритму.
