
- •Лекція № 5 Тема: Розв’язування алгебраїчних конгруенцій
- •1. Розв’язування квадратних конгруенцій за простим модулем
- •7.2) Обчислити , .
- •7.2) Обчислимо , .
- •Алгоритм Шенкса -Тонеллі
- •2. Алгебраїчні конгруенції -го степеня за простим модулем та способи їх розв'язування
- •1. Заміна коефіцієнтів абсолютно найменшими лишками за модулем .
- •2.Зниження степеня конгруенції.
- •3. Перехід до еквівалентної конгруенції, старший коефіцієнт якої дорівнює 1.
- •3. Число розв’язків конгруенції -го степеня за простим модулем
- •4. Алгебраїчні конгруенції -го степеня за складеним модулем та способи їх розв'язування
- •5. Алгоритм Берлекемпа розкладання многочлена на незвідні множники над скінченним полем
- •Алгоритм Берлекемпа (Berlecamp’s Algorithm)
Алгоритм Шенкса -Тонеллі
Обчислити значення символу Лежандра . Якщо , – квадратичний лишок, якщо , – квадратичний нелишок
Записати число у вигляді добутку парного і непарного чисел: , .
Знайти випадковий квадратичний нелишок за модулем , тобто для виконано співвідношення .
Покласти .
Обчислити
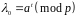 ,
,
 .
.
Обчислити порядок
 ,
який є дільником
,
який є дільником
 ,
тобто
,
тобто
 (порядком
називається число
(порядком
називається число
 таке, що
таке, що
 ).
).Обчислити степінь
 , в який треба підносити
, в який треба підносити
 :
:
 .
.Обчислити
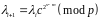 ,
,
 ,
,
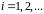
Якщо
при деякому
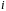 порядок
порядок
 виявиться рівним 1, то
виявиться рівним 1, то
 – шуканий корінь.
– шуканий корінь.
Приклад 2. Розв’язати конгруенцію:
Розв’язання.
Обчислимо значення символу Лежандра
Отже, конгруенція має розв’язки.
Запишемо число у вигляді добутку парного і непарного чисел: . Отже, , .
Знайдемо квадратичний нелишок за модулем . Нехай , тому що
.
Покладемо
 .
.Обчислимо
 ,
,

Обчислимо порядок :
 .
.
Звідси,
 ,
,
 .
.
Обчислимо степінь , в який треба підносити :
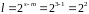 .
.Обчислимо


9) Перевірка: .
2. Алгебраїчні конгруенції -го степеня за простим модулем та способи їх розв'язування
Нехай задано конгруенцію
 , (3)
, (3)
або скорочено
 ,
,
де
 – просте число,
– просте число,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Перед розв’язуванням таких конгруенцій, їх спрощують: замінюють коефіцієнтів абсолютно найменшими лишками за модулем , знижують степінь конгруенції, переходять до еквівалентної конгруенції, старший коефіцієнт якої дорівнює 1.
Розглянемо детально способи спрощення таких конгруенцій.
1. Заміна коефіцієнтів абсолютно найменшими лишками за модулем .
Нехай
 ,
,
 ,
де
,
де
 – абсолютно найменший або найменший
невід'ємний лишок за модулем
.
Тоді
– абсолютно найменший або найменший
невід'ємний лишок за модулем
.
Тоді
 і конгруенція (3) еквівалентна конгруенції
і конгруенція (3) еквівалентна конгруенції
 .
.
Приклад 1. Спростити конгруенцію
 ,
,
зменшивши коефіцієнти за абсолютною величиною.
Розв’язання.
Маємо:
 ,
,
 ,
,
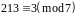 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
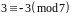 .
Отже, задана конгруенція еквівалентна
конгруенції
.
Отже, задана конгруенція еквівалентна
конгруенції
 .
.
2.Зниження степеня конгруенції.
Можливі випадки:
а)
 .
Тоді
.
Тоді
 не може набувати значень, кратних
,
тобто
не може набувати значень, кратних
,
тобто
 ,
значить
,
значить
 .
За теоремою Ферма
.
За теоремою Ферма
 .
Якщо
.
Якщо
 таке, що
таке, що
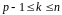 ,
то, поділивши з остачею
,
то, поділивши з остачею
 на
на
 ,
маємо:
,
маємо:
 ,
де
,
де
 ,
,
 .
Тоді
.
Тоді
 .
.
Замінивши
в конгруенції (3) доданки
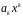 на конгруентні їм
на конгруентні їм
 ,
приходимо до конгруенції степеня меншого
за
,
приходимо до конгруенції степеня меншого
за
 ,
яка еквівалентна конгруенції (3).
,
яка еквівалентна конгруенції (3).
Приклад 2. Спростити конгруенцію
,
знизивши її степінь.
Розв’язання.
Помічаємо, що
 не є розв’язком даної конгруенції,
значить
не є розв’язком даної конгруенції,
значить
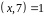 .
Тоді за теоремою Ферма
.
Тоді за теоремою Ферма
 .
Враховуючи це, маємо:
.
Враховуючи це, маємо:
 ;
;
 ;
;
 ;
;
 .
.
Отже, задана конгруенція еквівалентна конгруенції
 ,
,
яку після зведення подібних доданків запишемо у вигляді:
 .
.
а)
 для всіх
для всіх
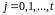 ,
де
,
де
 ,
,
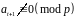 .
.
Конгруенцію (4) можна записати у вигляді:
 ,
,
або у вигляді:
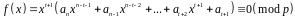 .
.
Остання конгруенція еквівалентна сукупності конгруенцій

і
 .
.
Оскільки , то, виконуючи перетворення випадку а), останню конгруенцію зведемо до еквівалентної конгруенції
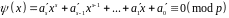
степеня, меншого за .
Тоді конгруенція (3) еквівалентна сукупності конгруенцій
і
або конгруенції
 ,
,
степеня, меншого за .
Приклад 3. Спростити конгруенцію
 ,
,
знизивши її степінь.
Розв’язання. Запишемо дану конгруенцію у вигляді
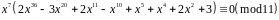 .
.
Очевидно, дана конгруенція еквівалентна сукупності конгруенцій

і
 .
.
Оскільки
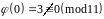 ,
то
,
то
 ,
значить
,
значить
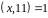 .
В силу тереми Ферма
.
В силу тереми Ферма
 .
Тоді остання конгруенція еквівалентна
конгруенції
.
Тоді остання конгруенція еквівалентна
конгруенції
 ,
,
яку після зведення подібних доданків запишемо у вигляді:

степеня, меншого за .
Тоді дана конгруенція еквівалентна сукупності конгруенцій
і
або конгруенції
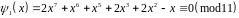 .
.
Теорема. Конгруенція , степінь якої не менше простого модуля , еквівалентна конгруенції, степінь якої менше .
Приклад 4. Розв’язати конгруенцію
 ,
,
Розв’язання.
Маємо
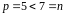 .
Помічаємо, що
.
Помічаємо, що
 не є розв’язком даної конгруенції,
значить
не є розв’язком даної конгруенції,
значить
 .
Тоді за теоремою Ферма
.
Тоді за теоремою Ферма
 .
Враховуючи це, маємо:
.
Враховуючи це, маємо:
 ;
;
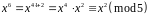 ;
;
 .
.
Отже, задана конгруенція еквівалентна конгруенції
 ,
,
яку після зведення подібних доданків запишемо у вигляді:
 ,
,
звідки
 ,
,
 ,
,
 .
.
