4. Алгебраїчні конгруенції -го степеня за складеним модулем та способи їх розв'язування

Теорема. Якщо 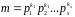– канонічний розклад модуля на множники, то алгебраїчна конгруенція -го степеня за складеним модулем

, (4)

еквівалентна системі конгруенцій

(5)

і число розв’язків конгруенції (за модулем ) (4) дорівнює добутку чисел розв’язків конгруенцій (5) (кожен з розв’язків за відповідним модулем).

Можливі наступні випадки розв’язування конгруенції (4):

1. Модуль конгруенції (4) має лише прості множники . Якщо відповідна система (5) сумісна, то число розв’язків конгруенції (за модулем ) (4) дорівнює добутку чисел розв’язків конгруенцій (5) (кожен з розв’язків за відповідним модулем). Розв’язуючи систему (5), розв’яжемо спочатку кожну конгруенцію окремо, потім знайдені розв'язки скомбінуємо між собою.

Приклад 1. Розв’язати конгруенцію

.

Розв’язання. Канонічний розклад модуля . Тому дана конгруенція еквівалентна системі конгруенцій

Розв’яжемо кожну конгруенцію системи окремо.

1)

Знизимо степінь конгруенції. Помічаємо, що не є розв’язком даної конгруенції, значить . Тоді за теоремою Ферма . Враховуючи це, маємо:

;

;

.

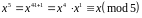Отже, маємо еквівалентну конгруенцію

,

яку після зведення подібних доданків запишемо у вигляді:

,

звідки , , , .

2)

Знизимо степінь конгруенції. Помічаємо, що не є розв’язком даної конгруенції, значить . Тоді за теоремою Ферма . Враховуючи це, маємо:

;

;

;

.

Отже, маємо еквівалентну конгруенцію

,

яку після зведення подібних доданків запишемо у вигляді:

,

звідки , .

3) Після цього складемо систему конгруенцій:

яку розв’яжемо за китайською теоремою про остачі:

.

2. Модуль конгруенції (5) має вигляд , де – просте число.

Спочатку розв’яжемо конгруенцію за простим модулем

.

Припустимо, що вона має розв'язки , де . Розкладемо функцію у ряд Тейлора:

Усі члени даного ряду, починаючи з третього, діляться на . Отже, конгруенція має місце при

.

Значення ділиться на , тому що – розв'язок конгруенції за модулем . Із знайденої конгруенції легко визначити за умови, що не ділиться на :

Розв’язком останньої конгруенції буде , , де 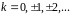. Тоді

,

де . В результаті . Підставимо це значення замість в даний многочлен і знову розкладемо функцію у ряд Тейлора:

Усі члени даного ряду, починаючи з третього, діляться на . Звідси випливає, що весь многочлен ділиться на тоді, коли вираз ділиться на . Отже, конгруенція має місце при

.

Значення ділиться на , тому що – розв'язок конгруенції за модулем . Із знайденої конгруенції легко визначити за умови, що не ділиться на :

.

Розв’язком останньої конгруенції буде , , де . Підставивши це значення у вираз для , дістанемо загальний розв'язок за модулем :

де .

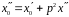Продовжуючи аналогічним чином, дійдемо до конгруенції за модулем , тобто дістанемо розв'язок вихідної конгруенції за цим модулем.

Приклад 1. Розв’язати конгруенцію

.

Розв’язання. Канонічний розклад модуля .

1) Спочатку розв’яжемо конгруенцію за простим модулем 3

,

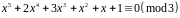спростивши яку, отримаємо , звідки

, , ,

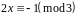або , де .

Розкладемо функцію у ряд Тейлора:

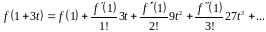
Усі члени даного ряду, починаючи з третього, діляться на 9. Визначимо з конгруенції:

.

; .

,

звідки , , , тому

, де

3. Складемо конгруенцію за модулем 27 і розв’яжемо відносно :

.

, , ,

, , де .

Далі визначимо значення , яке задовольняє вихідну конгруенцію за модулем 27:

.

Отже, розв’язком конгруенції є .